Research codes

symBvN: Algorithms for symmetric Birkhoff-von Neumann decomposition

Damien Lesens and Bora Uçar. From the paper Algorithms for symmetric Birkhoff-von Neumann decomposition of symmetric doubly stochastic matrices, Damien Lesens, Bora Uçar, and Jérémy E. Cohen.

RR-9566, Inria Lyon. 2025

Tech report bibtex codes

We investigate the symmetric Birkhoff-von Neumann decomposition of symmetric doublmy stochastc matrices. Our algorithms write a given symmetric doubly stochastic matrix as a convex combination of symmetric permutation matrices (whenever possible).


SymBvN is possible and not
A symmetric doubly stochastic matrix without a symBvN decomposition; another symmetric doubly stochastic matrix which possesses a symBvN decomposition.

Bottled: Fast algorithms for the bottleneck matching problem

Ioannis Panagiotas, Grégoire Pichon, Somesh Singh, and Bora Uçar. Engineering fast algorithms for the bottleneck matching problem,

31th European Symposium on Algorithms (ESA 2023), Amsterdam, The Netherlands, September 4--9, 2023

Pre-perint bibtex codes

We investigate the maximum bottleneck matching problem in bipartite graphs. Given a bipartite graph with nonnegative edge weights, the problem is to determine a maximum cardinality matching in which the minimum weight of an edge is the maximum.


The first observation
The two vertex covers (touching all nonzeros of a matrix) readily identifed by the Dulmage-Mendelsohn decomposition, and their use to select better values.

Hyperedge queries

Jules Bertrand, Fanny Dufossé, Somesh Singh, and Bora Uçar. Algorithms and data structures for hyperedge queries, Inria Research Report RR-9390 (revised April 2022).

Tech. Rep. bibtex codes

We consider the problem of querying the existence of hyperedges in hypergraphs. More formally, we are given a hypergraph, and we need to answer queries of the form ``does the following set of vertices form a hyperedge in the given hypergraph?''. Our aim is to set up data structures based on hashing to answer these queries as fast as possible. We propose an adaptation of a well-known perfect hashing approach for the problem at hand. We analyze the space and run time complexity of the proposed approach, and experimentally compare it with the state-of-the-art hashing-based solutions. Experiments demonstrate the efficiency of the proposed approach with respect to the state-of-the-art.


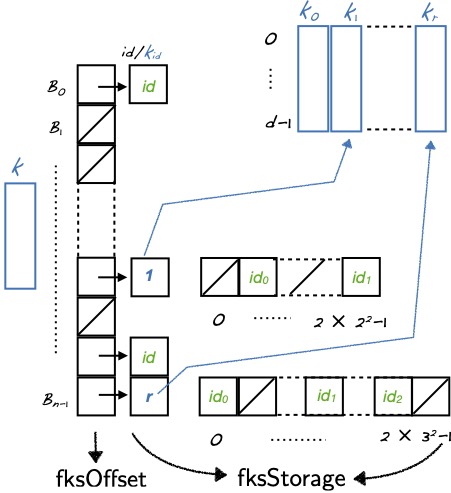
FKSlean structure
The contents of a bucket depend on the number of hyperedges mapped to it. If a bucket is empty, nothing is stored; if there is only one hyperedge, then the id of the hyperedge mapping there is stored; otherwise, the index of a suitable $d$-tuple from the shared set K is stored, along with a space of suitable size.

Karp--Sipser-based heuristics for matchings in hypergraphs

Fanny Dufossé, Kamer Kaya, Ioannis Panagiotas and Bora Uçar. Effective Heuristics for matchings in hypergraphs, in

Proceedings of SEA2 2019, Kalamata, Greece, June 24–29, pp. 248–-265, 2019

Paper Tech. Rep. bibtex codes

The problem of finding a maximum cardinality matching in a d-partite, d-uniform hypergraph is an important problem in combinatorial optimization and has been theoretically analyzed. We first generalize some graph matching heuristics for this problem. We then propose a novel heuristic based on tensor scaling to extend the matching via judicious hyperedge selections. Experiments on random, synthetic and real-life hypergraphs show that this new heuristic is highly practical and superior to the others on finding a matching with large cardinality.


Rule-1 of KS
Rule-1: There are d-1 vertices of degree-1 in a hyperedge.



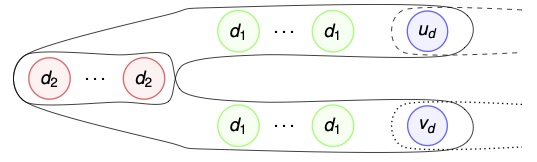
Rule-2 of KS
Rule-2: Two hyperedges have common vertices of degree-2 (shown with d2), each one of the two hyperedges has degree-1 vertices on the same dimensions (shown with d1), and the two hyperedges can differ at the last dimension (shown with ud and vd).

Fast almost optimal algorithms for bipartite matching

Ioannis Panagiotas and Bora Uçar. Engineering fast almost optimal algorithms for bipartite graph matching,

28th European Symposium on Algorithms (ESA 2020), Pisa, Italy., September 7--11, pp. 76:1--76:23, 2020

Paper Tech. Rep. bibtex codes

We consider the maximum cardinality matching problem in bipartite graphs. There are a number of exact, deterministic algorithms for this purpose, whose complexities are high in practice for large problem instances. There exist randomized approaches for special classes of bipartite graphs. Random 2-out bipartite graphs, where each vertex chooses two neighbors at random from the other side, form one class for which there is an O(m + n log n)-time Monte Carlo algorithm. Regular bipartite graphs, where all vertices have the same degree, form another class for which there is an expected O(m + n log n)-time Las Vegas algorithm. We investigate these two randomized algorithms, and turn them into practical heuristics applicable to all bipartite graphs. We compare the performance of the resulting heuristics and show that they can obtain near optimal results in practice and are comparable with the standard approaches.


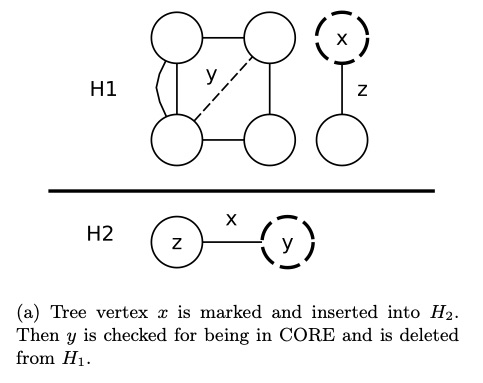
Monte Carlo on 2-out

Karp--Sipser reductions

Kamer Kaya, Johannes Langguth, Ioannis Panagiotas, and Bora Uçar. Karp-Sipser based kernels for bipartite graph matching, in

ALENEX20: SIAM Symposium on Algorithm Engineering and Experiments, Jan 2020, Salt Lake City, Utah, US.

paper bibtex codes

We consider Karp-Sipser, a well known matching heuristic in the context of data reduction for the maximum cardinality matching problem. We describe an efficient implementation as well as modifications to reduce its time complexity in worst case instances, both in theory and in practical cases. We compare experimentally against its widely used simpler variant and show cases for which the full algorithm yields better performance.

The codes are for bipartite and also for general undirected graphs.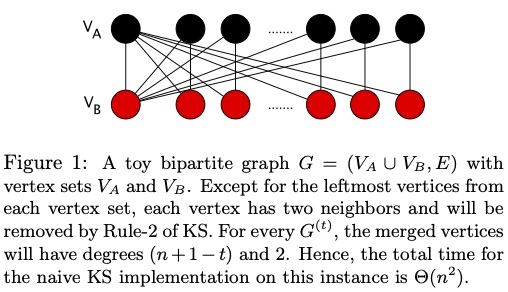

Karp--Sipser rule-2

Acyclic partitioning of DAGs

Julien Herrmann, M. Yusuf Ozkaya, Bora Uçar, Kamer Kaya, and Ümit V. Çatalyürek. Multilevel algorithms for acyclic partitioning of directed acyclic graphs,

SIAM Journal on Scientific Computing, 41(4), pp. A2117--2145, 2019

paper bibtex codes

We investigate the problem of partitioning the vertices of a directed acyclic graph into a given number of parts. The objective function is to minimize the number or the total weight of the edges having end points in different parts, which is also known as the edge cut. The standard load balancing constraint of having an equitable partition of the vertices among the parts should be met. Furthermore, the partition is required to be acyclic; i.e., the interpart edges between the vertices from different parts should preserve an acyclic dependency structure among the parts. In this work, we adopt the multilevel approach with coarsening, initial partitioning, and refinement phases for acyclic partitioning of directed acyclic graphs. We focus on two-way partitioning (sometimes called bisection), as this scheme can be used in a recursive way for multiway partitioning. To ensure the acyclicity of the partition at all times, we propose novel and efficient coarsening and refinement heuristics. We also propose effective ways to use the standard undirected graph partitioning methods in our multilevel scheme.


(a) A graph and (b) cyclic and convex partition (c) cyclic and convex partition (d) Acyclic and convex partition

MatchMaker: Efficient algorithms for the maximum cardinality matching problem in bipartite graphs

Iain S. Duff, Kamer Kaya, and Bora Uçar. Design, implementation, and analysis of maximum transversal algorithms,

ACM Transactions on Mathematical Software, 38 (2), pp. 13:1--13:31, 2011.

Kamer Kaya, Johannes Langguth, Fredrik Manne, and Bora Uçar, Push-relabel based algorithms for the maximum transversal problem,

Computers and Operations Research, 40 (5), pp. 1266--1275, 2013.

paper (Duff et al.) bibtex (Duff et al.) paper (Kaya et al.) bibtex (Kaya et al.) codes
Archieved at Software Heritage

We report on careful implementations of ten algorithms for solving the problem of finding a maximum transversal of a sparse matrix. We analyze the algorithms and discuss the design choices. We use a common base to implement all of the algorithms and compare their relative performance on a wide range of graphs and matrices. We systematize, develop, and use several ideas for enhancing performance. We conclude that a carefully tuned push-relabel algorithm is competitive with all known augmenting path-based algorithms, and superior to the pseudoflow-based ones.

[Version 2 (2013) matchmaker2 provides implementations on a GPU.]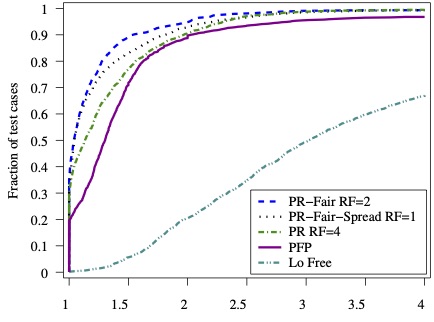

Push-relabel, pseudo-flow, and augmenting path comparison.

LibSpMxV: Parallel, MPI-based sparse matrix--vector multiplication

Kamer Kaya, Bora Uçar, and Ümit V. Çatalyürek. Analysis of partitioning models and metrics in parallel sparse matrix-vector multiplication,

in PPAM 2013, Parallel Processing and Applied Mathematics , 2013.

paper bibtex codes

We provide parallel matrix--vector multiply routines for 1D and 2D partitioned sparse square and rectangular matrices, given the partitions on the input- and output-vectors and the matrix nonzeros. The codes include building blocks (some vector operations) of parallel, MPI-based implementation of iterative methods for solving sparse linear systems. The library overlaps communucation and computation to the maximum extent possible (for a given partition).

See also a supporting technical report. A previous version is discussed in another techical report.


Parallel SpMxV