Bit-Vector Encodings of Hierarchies

Project

Hierarchical structures frequently occur in computer applications. In such structures, the elements are structured according to a partially ordered set (poset). For a poset (P,<), the reachability (also called comparability or subsumption) question consists in determining for two elements x and y whether x < y ? In order to answer these queries efficiently, special encodings (data structures and algorithms) have been designed for posets. They are called hierarchical  encodings. The usual requirements for these encodings are the runtime efficiency, so that tests should be fast, and the minimization of the space used to store the encoding.

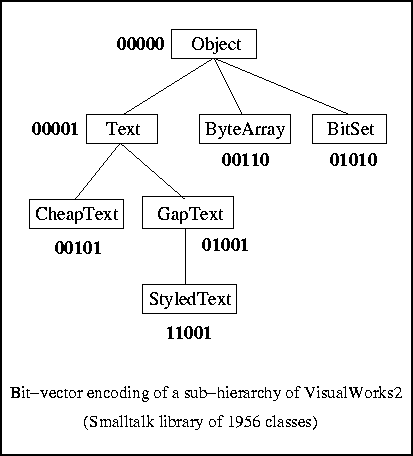
One idea to achieve these tests is to associate with each element of the poset a subset of a set S={1,...,k} such that the reachability question coincides with subset inclusion. These subsets can be represented by bit vectors of size k. For this reason, these encodings are called bit-vector encodings. They provide very compact encodings in terms of space and tests can be performed in "constant" time. Generating a encoding for a poset is equivalent to embedding this poset in the lattice of all the subsets of S (the hypercube of dimension k).

Our work consists in studying these encodings. In particular, the minimization of the size of the encoding is a difficult problem (NP-complete in the general case) and we interest in incremental aspects for evolving hierarchies. This work was run by Michel Habib, Lhouari Nourine, Olivier Raynaud and Eric Thierry in the Departement of Theoretical Computer Science (IFA) of the Laboratory of Computer Science, Robotics and Microelectronics of Montpellier (LIRMM). These encodings find applications in Object Oriented Languages,  Databases,  Knowledge Representation Systems.