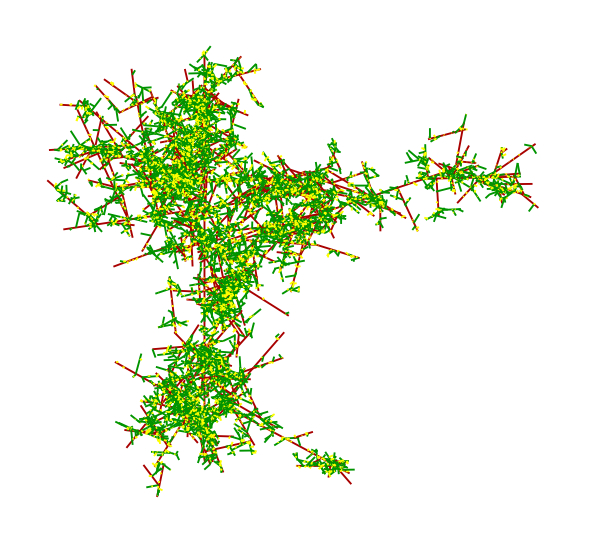
| Sur l'image suivante, nous voyons une simulation de l'arbre continu brownien, introduit par Aldous (Ann. Probab. 1991). On le construit à l'aide d'une mesure de Poisson sur la demi-droite réelle, d'intensité t*dt. Les atomes de cette mesure découpent la demi-droite en une suite infinie de segments consécutifs, et l'arbre s'obtient en greffant récursivement l'extrémité gauche de chaque segment en un point choisi uniformément dans l'union des segments qui le précèdent. Le dessin ci-contre a été obtenu par cette procédure, avec les 5000 premiers points du processus. Nous avons fait la construction dans l'espace tridimensionnel, en choisissant, à chaque branchement, une direction uniforme dans l'espace: ainsi, aucune des branches n'en croise une autre. Si l'unité de longueur est le diamètre de l'ensemble obtenu, nous avons colorié en rouge les segments de longueur plus grande que 0,05 unités, tandis que les segments entre 0,01 et 0,05 unités sont en vert, les plus petits sont en jaune. |

|
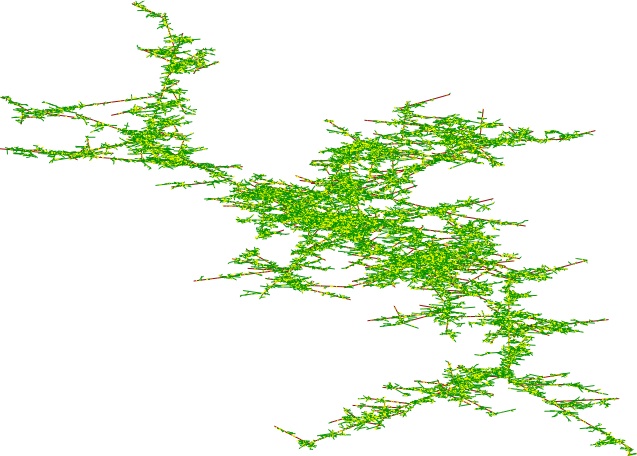
| Voici maintenant une simulation avec les 50000 premiers segments, on voit apparaître une structure très touffue. On peut montrer que la dimension de Hausdorff de cet objet (en fait, du complété de la réunion de tous les segments) est 2. |
|
|
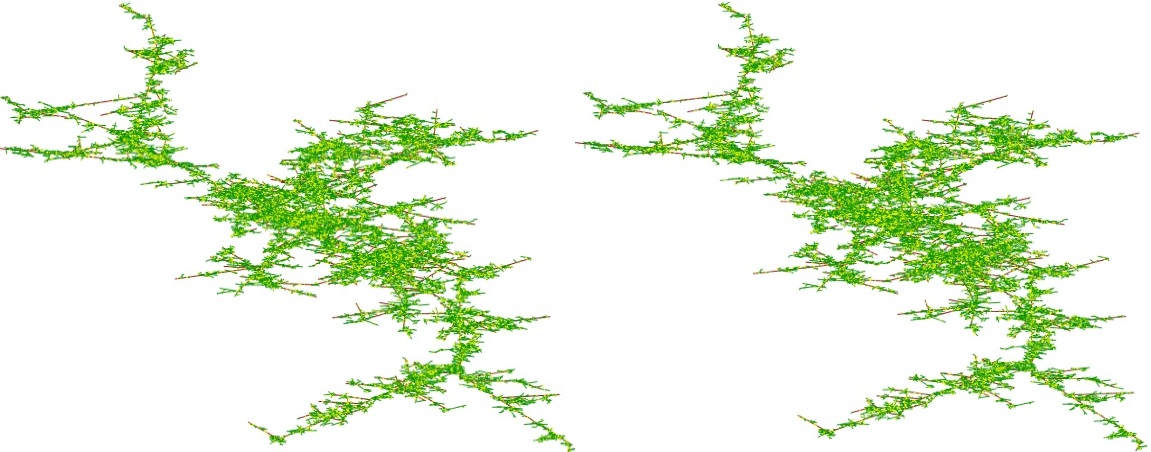
On perçoit moins l'effet de profondeur dans la dernière
image. Pour
cette raison, voici le même arbre ci-contre, en
stéréogramme. L'image de droite est obtenue
à partir de celle de gauche en la tournant longitudinalement
de 3 degrés. Le but de l'exercice est de fixer un point
à l'infini, de sorte que vos yeux fixent chacune des images
indépendamment. Les deux images doivent alors fusionner, et le
cerveau interprète la différence d'angle en termes de
profondeur.
Ce n'est pas toujours facile au début, voici un lien pour s'entraîner. Il faut trouver la bonne distance par rapport à l'écran pour que l'effet de profondeur soit optimal. Eventuellement, vous pouvez essayer en dézoomant un peu l'image, c'est plus facile. |
|
| Et pour finir, voici un gif animé avec les 50000 premiers segments. |

|