Index  
If you want to use my pictures (or my code), please contact me.

Brownian windings (orange for positive values, purple for negative ones)


Brownian weighted by its windings
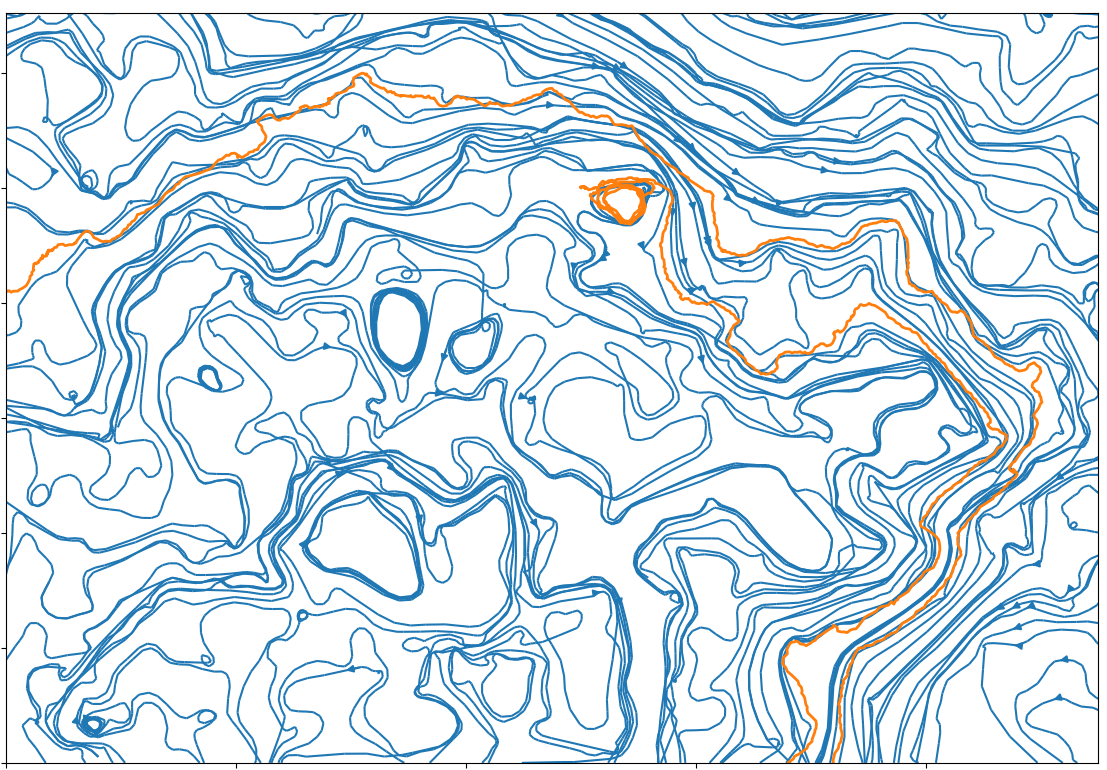
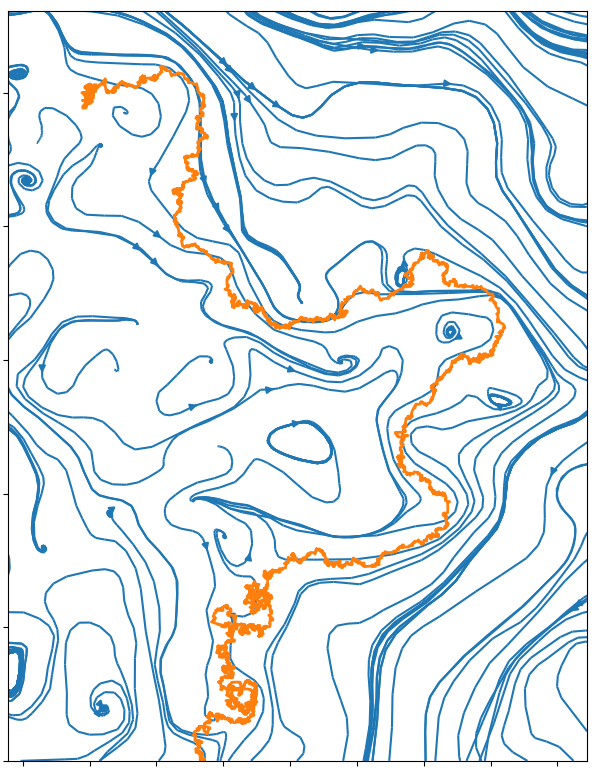
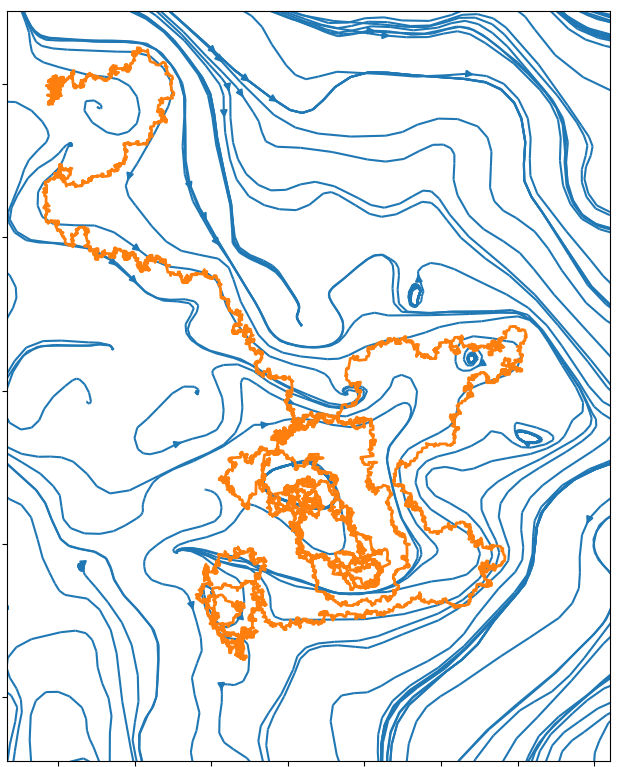
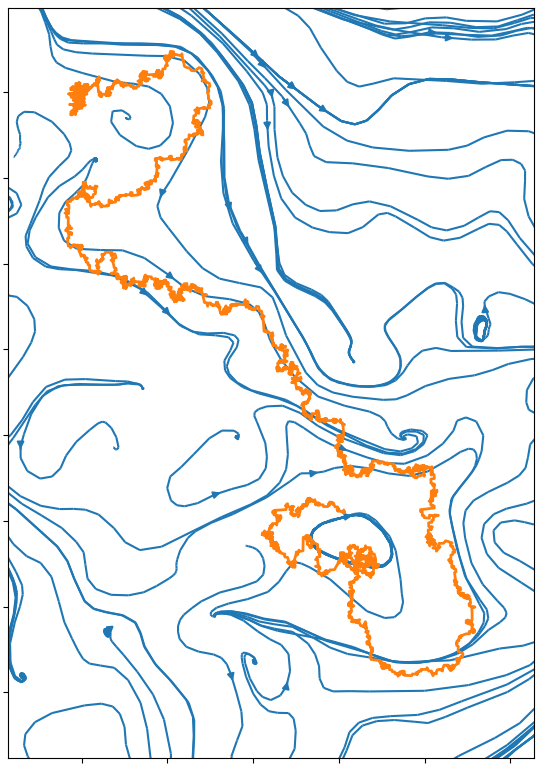
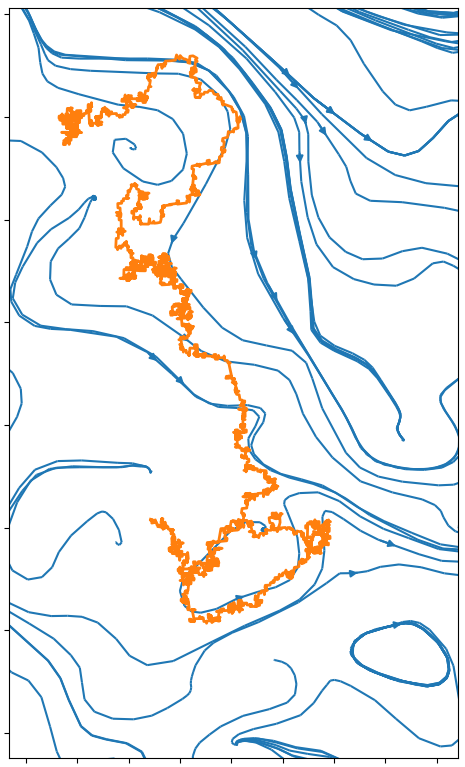
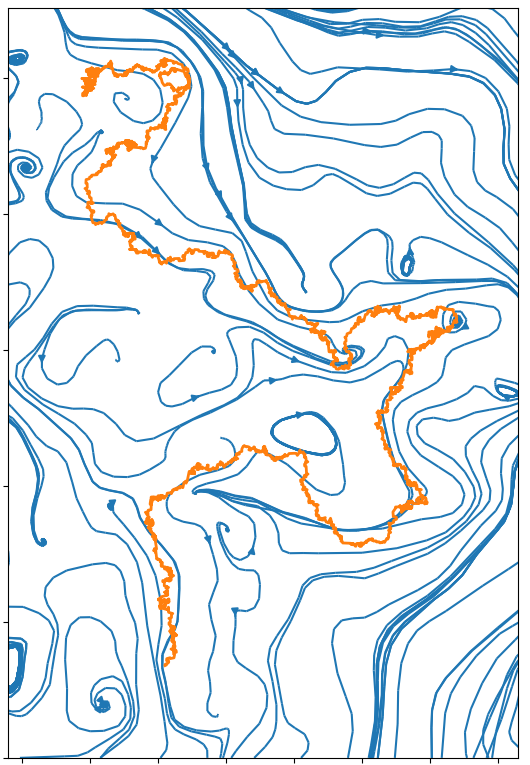
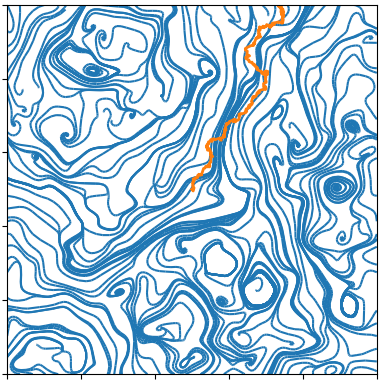
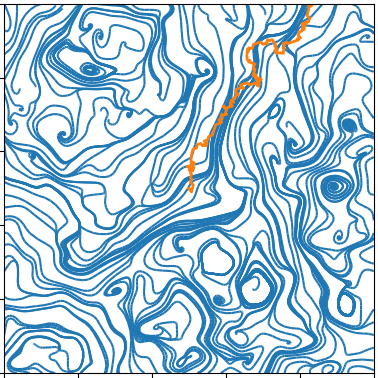
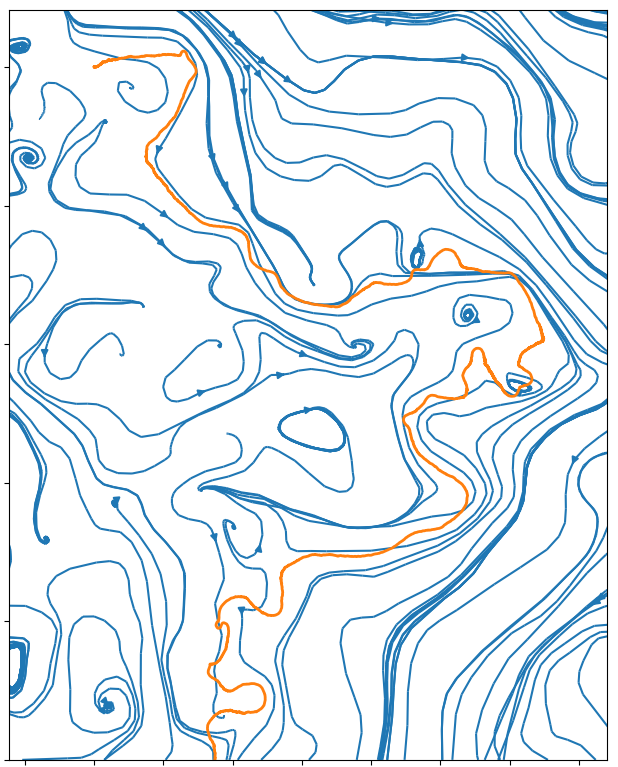
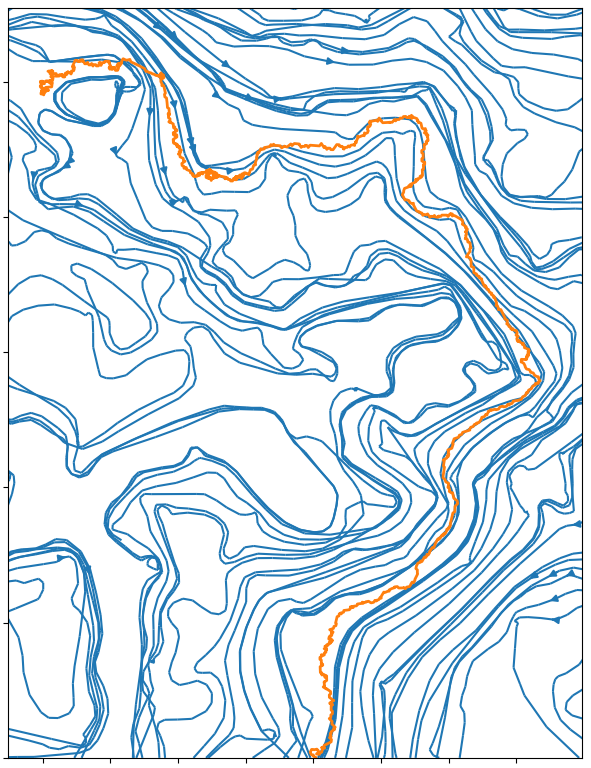
In the following pictures, the blue curves are the integral lines of a vector field A which is such that div A=0 and curl A is a white noise (actualy simulated as a signed Poissonian noise).
The orange curve is a random walk approximation discret version of dX_t=dW_t+c A_Xtd t.
When curl A becomes an actual white noise, and the random walk step goes to 0, I expect that the properly normalized limit should be an SLE(k) for function k of c.
Alternatively, X might describe the trajectory of an electron moving inside in a crystal with magnetic impurities.

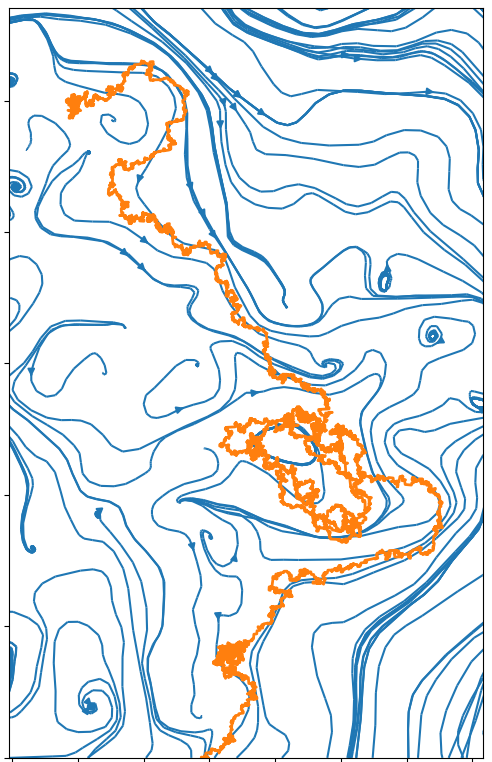
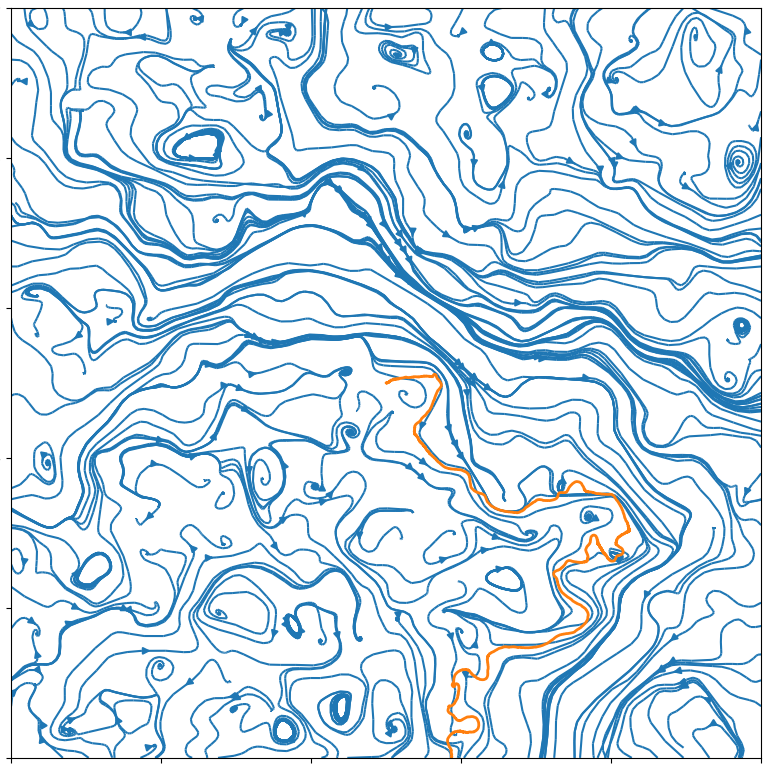
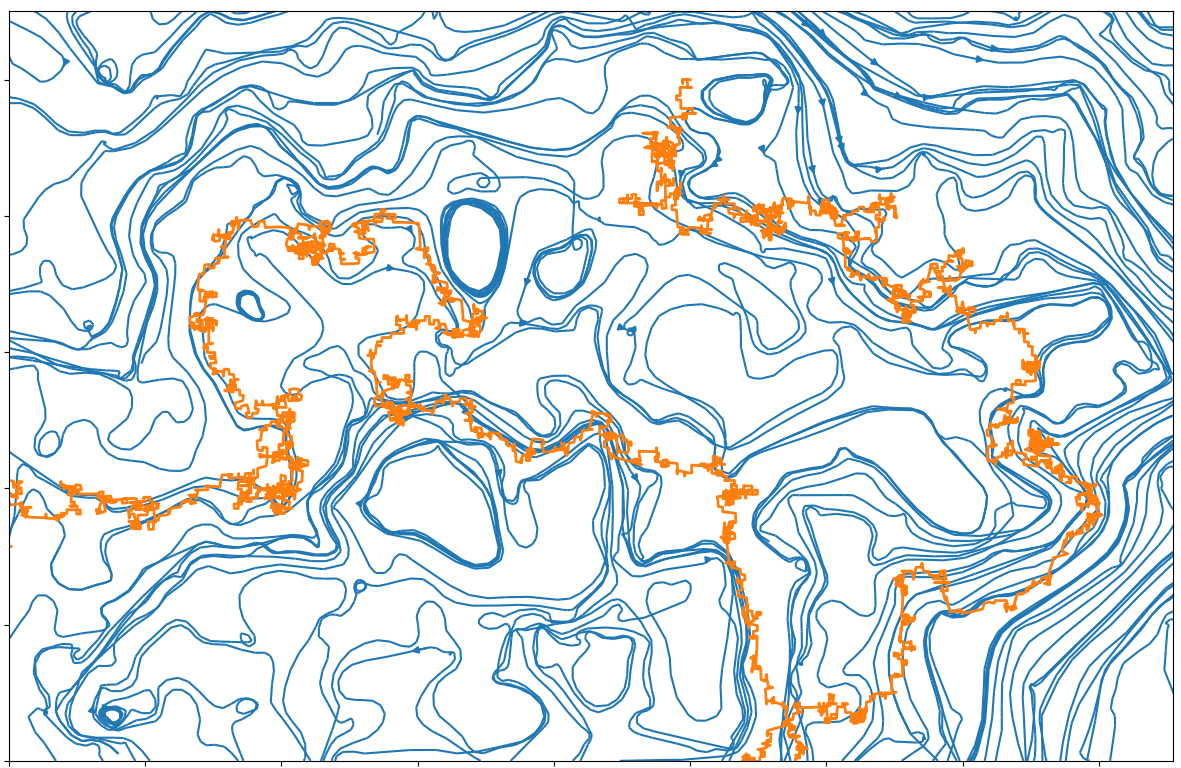
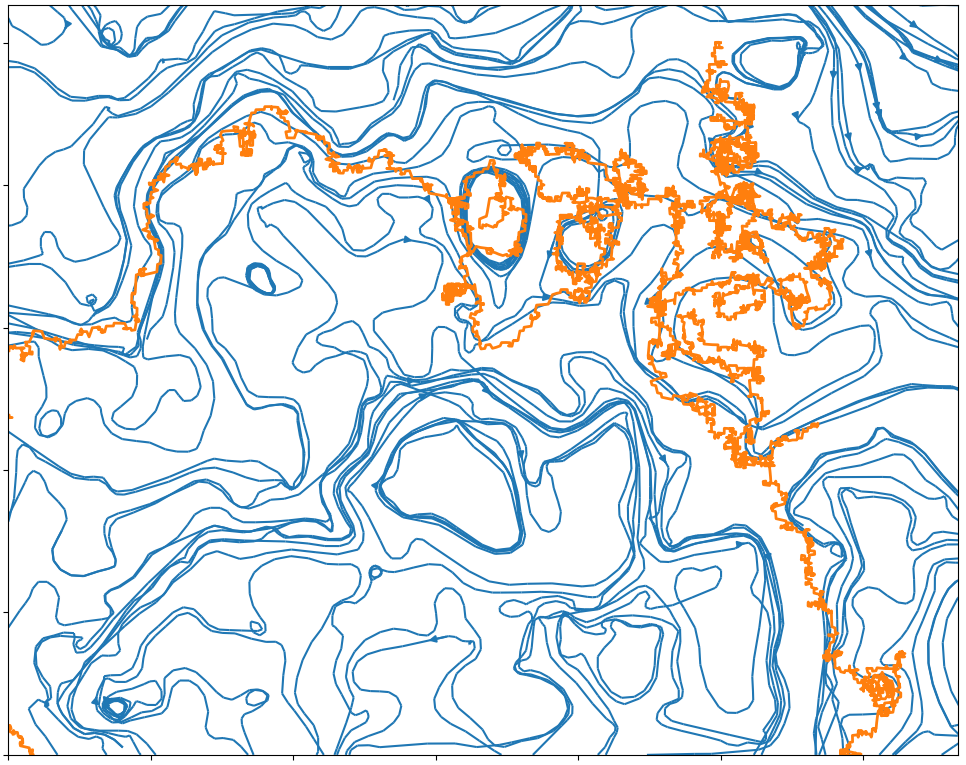
Here, the background color depends ('linear scale') on the norm of A, so the integral lines (still visible when one looks close enough) are run through faster when the background color is red.

Here are some more examples, but as PDF files. Loading time can be a bit long. The blue curves will load after the background, and their thickness depends on the level of zoom).