A single bead bouncing on a vibrating plate
Collaboration with
Claude Laroche
Introduction
We
considered experimentally the case of a single bead bouncing on a
vibrating plate. The plate oscillates sinusoidally along the
vertical with the peak acceleration, G, and the bead-plate collisions are characterized
by the velocity restitution coefficient, e. The situation has
already been realized experimentally by many different groups
since the early 50's. This system is probably one of the the most
simple in which the period doubling route to chaos is observed.
You can find a lot of informations on the subject in the nice
website proposed by
Piotr
Pieranski.
In order to discuss the thermalization of granular gases by
vibrating boundaries, we determined experimentally the mean
energy of the bead by tracking the bead-plate collision dates.
Results
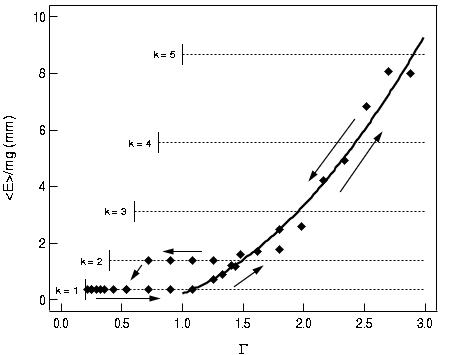
Above a threshold acceleration
Gs = 0.85, which does not depend on the
restitution coefficient, the bead energy is shown to initially
increase linearly with the vibration amplitude, A, whereas it is
found to scale like (Aw)2/(1-e) only in the limit
G>>Gs (Fig.1).

Fig.1: Energy <E> vs. peak plate acceleration G.
The
threshold acceleration Gs is shown to decrease when the bead is
subjected, in simulations, to additional non-dissipative
collisions occuring with the typical frequency
nc. As a
consequence, the bead energy scales like (Aw)2/(1-e) for all vibration
strength in the limit nc >> 1.4 (1-e)1.5 n where n is the frequency of the
plate oscillation. From the experimental and numerical findings,
we propose an analytical expression of the bead energy as a
function of the experimental parameters.
The
results
are
interesting
for
discussing
the
problem of
the
injection
of energy
by a
vibrating
boundary
in the
case of
2D granular gases.
Related publication
Energy of
a single
bead
bouncing
on a
vibrating
plate:
experiments
vs.
numerical
simulations,
Géminard J.-C.,
and
Laroche
C., Phys.
Rev. E,
68
(2003)
031305.