Free-standing smectic films : meniscus & edge dislocations
Collaboration with
Patrick
Oswald,
Frédéric
Picano, Robert
Holyst,
and
Andrzej
Zywocinski.
Meniscus
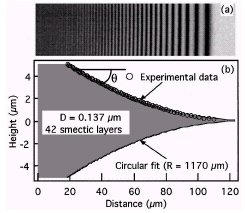
It is a common knowledge that, in mechanical equilibrium, an isotropic liquid in contact with air must have the same pressure as the air providing its interface is flat. This is not necessarily true in a smectic-A liquid crystal because its layers are elastic and can support a normal stress s that will equilibrate any pressure difference provided it is not too large. The pressure difference DP contributes to the tension of a freely suspended smectic film as shown experimentally by Pawel Pieranski et al. To produce a film, we draw out one side of a rectangular frame whose sides are wet due to a droplet of smectic-A liquid crystal. The film is observed with a video camera via reflected light microscopy. The pressure difference DP is measured from a detailed analysis of the shape of the meniscus that connects the film with the edges (Fig.1).
Fig.1:
Image of
the
meniscus
and
reconstruction
of the
meniscus
profile.
In an
isotropic
liquid,
the
meniscus
profile is
expected
to be
exponential.
In a Sm-A
liquid
crystal,
the
meniscus
profile is
circular,
and the
pressure
difference
DP
is simply
given by
Laplace
equation
DP
=
g/R,
where
g
is the
surface
free
energy and
R the
radius of
curvature
(see Géminard
et al,
1997, for
details).
Edge dislocations : Line tension and mobility
It is possible to produce an edge-dislocation loop in a horizontal smectic film at equilibrium: a thin heating wire in placed very close (50 mm) to the lower film surface. Sending an electric pulse of very short duration in the wire can nucleate a dislocation loop. The evolution with time of the radius of the loop (Fig.2) informs us about the line tension and mobility of the edge dislocation, provided that the pressure difference DP is known. We point out that the method makes possible to measure these quantities on an isolated dislocation.
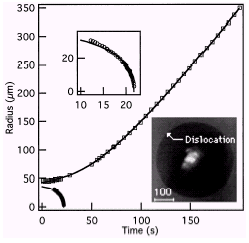
Fig.2:
Radius of
a
dislocation
loop vs.
time.
Depending
on its
initial
radius, a
dislocation
loop can,
either
collapse
and
disappear,
or grow
and reach
the edges
of the
supporting
frame. In
this last
case, the
film
thickness
is reduced
by the
Burgers'
vector
(inset:
image in
the
reflected
light
microscope.
The
heating
wire is
visible at
the center
of the
loop).
Edge dislocations : vertical films
Measurements of the pressure difference DP are fastidious and we never observe stable dislocation loops in horizontal smectic films (they either grow or collapse). We developed an alternative method that makes possible the study of the line tension without knowledge of the overpressure DP: when the film is vertical, the dislocation loop, submitted to gravity, rises up until it reaches the upper edge of the frame (Fig.3). At rest, the dislocation loop differs significantly from a circle and its shape, similar to that of a droplet in the gravity field, is governed by the competition between the line tension and gravity.
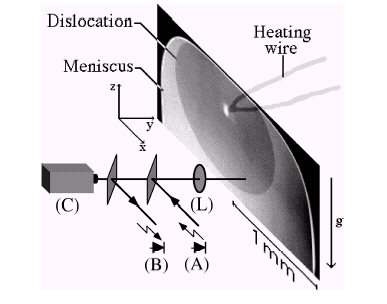
Fig.3:
Radius of
a
dislocation
loop vs.
time.
When the
smectic
film is
vertical,
the
dislocation
line rises
up and
reaches
the upper
edge of
the frame.
The
"equilibrium"
shape of
the
dislocation
gives
access to
the line
tension.
We showed,
using the
experimental
method,
that the
line
tension is
proportional
to the
Burgers'
vector in
smectic
liquid
crystals
(The line
tension
scales
like the
square of
the
Burgers'
vector in
solids).
Moreover,
its
increases
like
when the
film
thickness
d is
decreased
(Géminard
et al,
1998).
The same
method was
used to
study the
evolution
of the
line
tension
when the
transition
to the
nematic
phase is
approached
(Zywocinski
et al,
2000).
Since then...
Since the seminal work presented in this short summary, meniscus and dislocations in free-standing liquid crystal films have been the subject of Frédéric Picano's (ENS-Lyon, 2001) and François Caillier's (ENS-Lyon, 2005) PhD thesis . You can find more reliable information on this subject in the nice book "Smectic and Columnar Liquid Crystals" (volume 2) by Patrick Oswald and Pawel Pieranski.
Related publications
Meniscus and
dislocations in free-standing films of smectic A liquid crystals,
J. C. Géminard, R. Holyst and P. Oswald, Phys. Rev. Lett., 78
(1997) 1924-1927.
Experiments on
tracer diffusion in thin free-standing liquid-crystal films,
Bechhoefer J., Geminard J.-C., Bocquet L. and Oswald P., Phys.
Rev. Lett. 79 (1997) 4922.
Edge dislocation
in a vertical smectic-A film :
Line tension versus film thickness
and Burgers vector,
Géminard J.-C., Laroche C. and Oswald P., Phys. Rev. E 58
(1998) 5923.
Edge dislocation
in a vertical smectic A film :
line tension versus temperature
and film thickness near the nematic phase,
Zywocinski A., Picano F., Oswald P., and Géminard J.-C., Phys.
Rev. E 62 (2000) 8133.