La classification ascendante hiérarchique (CAH) sert à définir des classes d’individus à partir d’une ou plusieurs variables quantitatives.

La CAH s’accompagne de la construction d’un arbre de classification.

Un exemple: caractéristiques de 7 personnages

Considérons ce petit jeu de données:

data_orphan=read.table(paste(dat.path,"data_orphan.csv",sep=""),
                       sep=";",row.names=1,header=T)
print(data_orphan)

##        Sante Sante_Mentale Intellect Sociabilite Decision
## Sarah      8             8         7           4        6
## Alison     7             6         6           8        8
## Cosima     4             5         8           6        4
## Helena     8             2         5           3        6
## Rachel     8             5         6           2        6
## Katja      2             5         5           7        7
## Beth       8             4         7           5        7

Il renseigne des caractéristiques physiques et mentales de 7 personnages de la série « Orphan Black » (que je vous recommande). Pour ceux qui s’étonneraient de l’existence d’un tel jeu de données ou qui ne seraient pas d’accord avec son contenu (d’éventuels fans de la série?) : je précise que j’ai construit ce tout petit jeu de données (certes un peu subjectives) à des fins pédagogiques, et spécialement pour ce post…

On peut essayer de résumer graphiquement l’information concernant nos personnages en réalisant une ACP:

require(ade4)
monacp=dudi.pca(data_orphan,scannf=F,nf=2)
scatter(monacp)

Construction d’un arbre de classification

Pour rassembler les individus en construisant un arbre, on les assemble 2 à 2 en commençant par les individus les plus proches.

Ainsi, la construction de l’arbre de classification repose sur les distances entre individus:

table_distances=dist(data_orphan)
print(table_distances)

##           Sarah   Alison   Cosima   Helena   Rachel    Katja
## Alison 5.099020                                             
## Cosima 5.830952 5.830952                                    
## Helena 6.403124 6.855655 6.855655                           
## Rachel 3.741657 6.480741 6.324555 3.316625                  
## Katja  7.681146 5.385165 4.795832 7.874008 7.937254         
## Beth   4.242641 4.000000 5.291503 3.605551 3.464102 6.708204

Par défaut, la méthode utilisée pour calculer des distances entre les individus correspond à une distance euclidienne. Pour n variables X1, X2, X3, …,Xn la distance euclidienne entre les individus i et j est:

    $$ d_{i,j}=\sqrt{\sum_{k=1}^n (X_{k,i}-X_{k,j})^2}$$

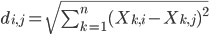
Ainsi, la distance entre (par exemple) Sarah et Alison peut se recalculer « à la main » de la manière suivante:

diffs_par_variable=data_orphan["Sarah",]-data_orphan["Alison",]
sqrt(sum(diffs_par_variable^2))

## [1] 5.09902

La construction de l’arbre de classification à partir du tableau des distances se fait de la manière suivante:

mon_arbre=hclust(table_distances,method="ward")
mon_arbre

## 
## Call:
## hclust(d = table_distances, method = "ward")
## 
## Cluster method   : ward.D 
## Distance         : euclidean 
## Number of objects: 7

plot(mon_arbre)

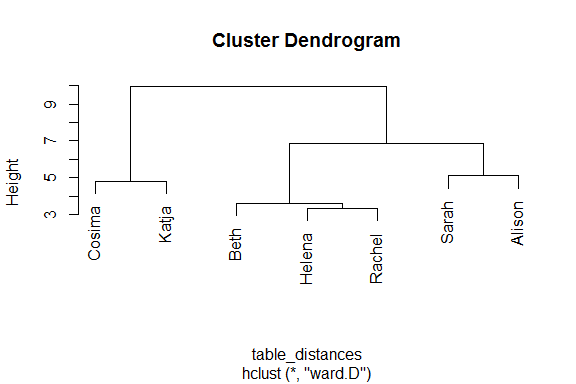
Construction d’un arbre de classification: explication

Pour vous expliquer comment se contruit, itérativement, un arbre de classification ascendante hiérarchique, je vais considérer non pas les données brutes, mais les scores issus de l’ACP réalisée plus haut (d’ailleurs, vous remarquerez que l’arbre en sortie n’est pas le même!). Cela va simplement me permettre de représenter graphiquement (en deux dimensions) les individus et à bien voir à quoi correspondent les distances entre deux individus.

Commençons avec l’ensemble des individus (ci-dessous).

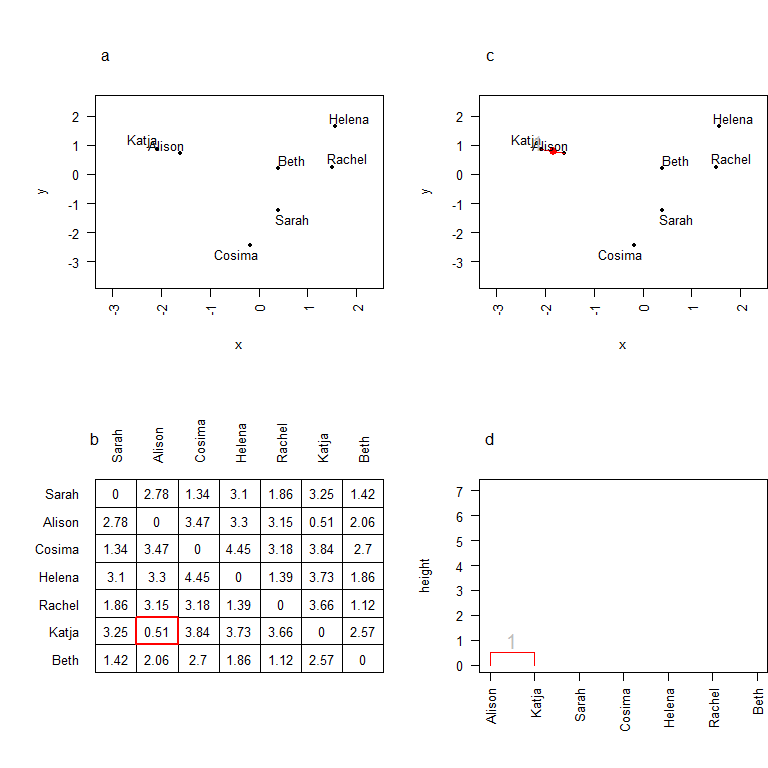
On représente ces individus dans l’espace factoriel (a). Si l’on calcule les distances deux-à-deux entre les individus (b), on se rend compte que les deux individus les plus proches sont Katja et Alison, puisqu’elles sont séparées de 0.51 seulement. On regroupe donc ces deux individus en un cluster (c), sobrement baptisé 1. On calcule des coordonnées pour ce cluster: elles correspondent en fait aux coordonnées de son barycentre. On peut en outre commencer à construire l’arbre de classification (d) en regroupant ces deux individus par une branche dont le noeud se situe à une hauteur correspondant à la distance entre les deux individus.

Poursuivons le processus:

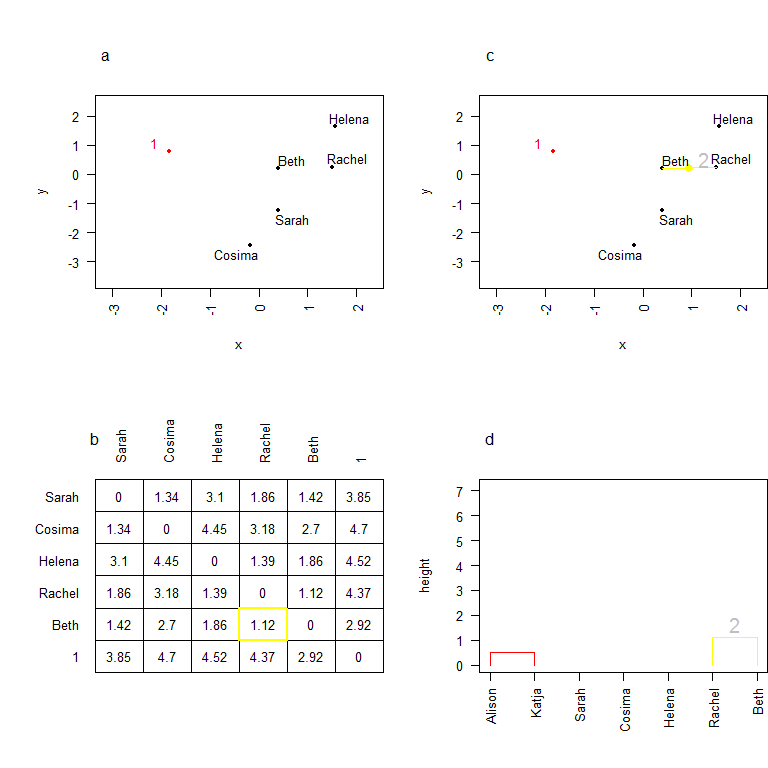
On a maintenant 6 individus (5 personnes et un cluster). Ces individus sont tous associés à des coordonnées dans l’espace, on peut donc sans difficulté calculer les distances deux-à-deux les séparant (b). Ici Rachel et Beth sont les deux individus les plus proches, on les regroupe donc en un cluster 2. On calcule les coordonnées de ce cluster, et on continue à construire l’arbre de classification (d). La hauteur du noeud correspond, encore une fois, à la distance entre Rachel et Beth, i.e. 1.12.

Poursuivons le processus:

On considère maintenant 5 individus (3 personnes, 2 clusters). Ici, les deux individus les plus proches sont Cosima et Sarah, on les regroupe donc en un cluster 3, dont on calcule les coordonnées. On continue à construire l’arbre de classification en rajoutant le troisième noeud (d).

Poursuivons le processus:

Désormais, on considère 4 individus (1 personne et 3 clusters). Les deux individus les plus proches sont Helena, et le cluster 2. On regroupe ces deux individus en un cluster 4. On calcule les nouvelles coordonnées de ce cluster. Remarquez que le barycentre n’est pas à mi-chemin entre Helena et le cluster 2 (c). En effet, il y a deux personnes dans le cluster 2, et Helena est seule: l’utilisation du barycentre retranscrit le « poids » plus important du cluster 2 dans l’établissement des coordonnées du cluster. On poursuit la construction de l’arbre (d).

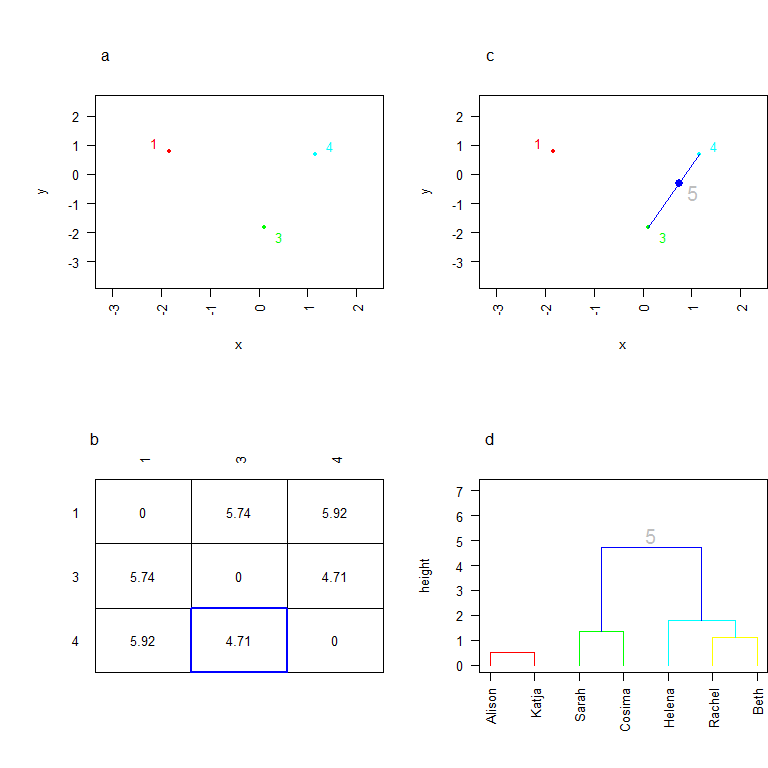
On considère maintenant 3 individus (3 clusters). Les deux clusters les plus proches sont le cluster 3 et le cluster 4. On crée donc un cluster 5 qui les réunit, et on calcule ses coordonnées. Le cluster 4 comptant un individu de plus que le cluster 3, le barycentre est plus proche de 4 que de 3!

Poursuivons le processus:

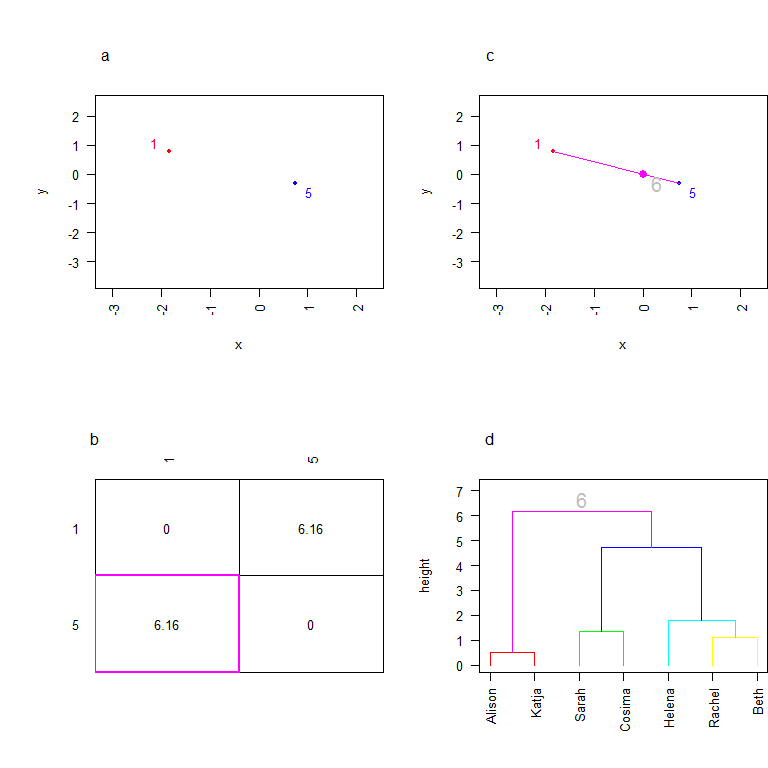
Ouf! on arrive à la fin (vous avez dû comprendre, à ce stade, l’intérêt de n’avoir que 7 individus dans mon jeu de données d’exemple…). On regroupe les deux clusters qui restent en plaçant un noeud à une hauteur qui correspond à leur distance. Et notre arbre est fini!

Ici, j’ai calculé une distance euclidienne, et j’ai calculé les nouvelles coordonnées par la méthode de Ward (les deux sont choisis par défaut lorsque l’on fait appel à la fonction hclust). Néanmoins, d’autres possibilités existent! Pour en prendre connaissance, je vous invite à consulter le fichier d’aide associé à la fonction hclust.