
Qu'est-ce que c'est ?
Il y a quelques mois, je vous proposais un billet sur les arbres décisionnels. Comme on dit, c'était l'arbre qui cachait la forêt (ha!ha! quelle joie d'avoir un blog pour pouvoir faire de tels jeux de mots). Voici donc la suite naturelle de ce billet,cette fois sur les forêts d'arbres décisionnels ou forêts aléatoires (alias "random forests" en anglais).
Les forêts aléatoires sont composées (comme le terme "forêt" l'indique) d'un ensemble d'arbres décisionnels. Ces arbres se distinguent les uns des autres par le sous-échantillon de données sur lequel ils sont entraînés. Ces sous-échantillons sont tirés au hasard (d'où le terme "aléatoire") dans le jeu de données initial.
On va utiliser le package randomForest.
require(randomForest)
On utilise le jeu de données iris:
data(iris)
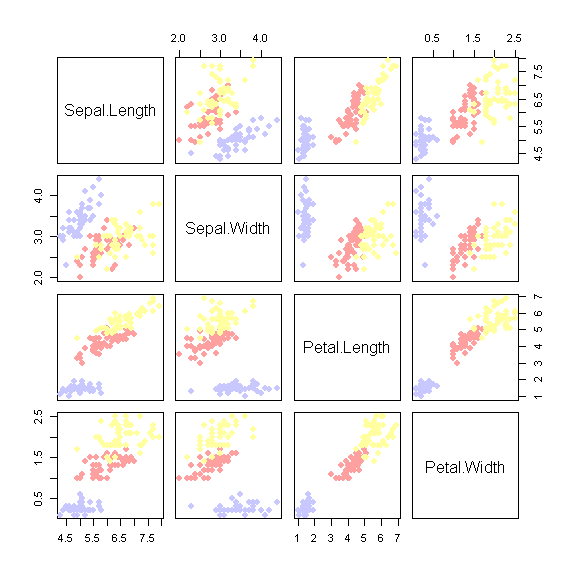
Dans ce jeu de données, des iris de trois espèces différentes sont décrits par :
- leur appartenance à l'espèce setosa (en gris ci-dessus), versicolor (en rose), ou virginica (en jaune)
- la longueur des sépales (les sortes de petites feuilles à la base des corolles de fleurs)
- la largeur des sépales
- la longueur des pétales
- la largeur des pétales
Construction d'une forêt aléatoire
Pour produire une forêt aléatoire (ici sans modifier les paramètres par défaut) à l'aide de la fonction randomForest, rien de plus simple:
iris.rf <- randomForest(iris[,1:4], iris$Species)
print(iris.rf)
##
## Call:
## randomForest(x = iris[, 1:4], y = iris$Species)
## Type of random forest: classification
## Number of trees: 500
## No. of variables tried at each split: 2
##
## OOB estimate of error rate: 4.67%
## Confusion matrix:
## setosa versicolor virginica class.error
## setosa 50 0 0 0.00
## versicolor 0 47 3 0.06
## virginica 0 4 46 0.08
Ici la fonction print nous permet d'afficher quelques caractéristiques de l'objet produit. On apprend ainsi que la forêt est composée de 500 arbres, qu'à chaque noeud l'algorithme fait un essai sur 2 variables, que le taux d'erreur est de 4%. La matrice de confusion est également affichée (on y reviendra très bientôt!).
Chaque arbre de la forêt est construit sur une fraction ("in bag") des données (c'est la fraction qui sert à l'entraînement de l'algorithme. Alors pour chacun des individus de la fraction restante ("out of bag") l'arbre peut prédire une classe.
Pour ce qui est de la construction de l'arbre lui-même, je vous renvoie une fois encore à ce billet.
Par défaut, la fonction randomForest tire au hasard n individus parmi les n (avec remplacement, ce qui devrait correspondre, en moyenne, à l'échantillonnage au hasard de 63.2% des individus). Ainsi sur les n = 500 arbres, chaque individu fera partie de la fraction "in bag" et "out of bag" en moyenne 0.632 500 = 316 et 0.368 500 = 184 fois (en moyenne, mais pas forcément exactement, du fait de l'aléa d'échantillonnage).
On peut ainsi accéder au nombre de fois où chaque individu est "out of bag" de la manière suivante (ici je n'affiche que les dix premiers individus):
print(iris.rf$oob.times[1:10])
## [1] 178 182 183 178 195 177 185 187 200 176
Sur l'ensemble des arbres sur lesquels les individus ont été "out of bag", on peut s'intéresser à la proportion de votes que chaque classe a recueilli. Ici, par exemple, je m'intéresse à un sous-échantillon de trois individus:
sous_echant=c(25,75,135)
iris$Species[sous_echant]
## [1] setosa versicolor virginica
## Levels: setosa versicolor virginica
iris.rf$oob.times[sous_echant]
## [1] 185 197 189
iris.rf$votes[sous_echant,]
## setosa versicolor virginica
## 25 1 0.0000000 0.000000000
## 75 0 0.9949239 0.005076142
## 135 0 0.5026455 0.497354497
Pour les trois individus affichés ci-dessus:
- la forêt aléatoire a classé le 1er individu en "setosa" (donc correctement) dans 100% des 185 arbres où il était "out of bag"
- la forêt aléatoire a classé le 2ème individu en "versicolor" (donc correctement) dans 99% des 197 arbres où il était "out of bag".
- la forêt aléatoire a classé le 3ème individu en "virginica" (donc correctement) dans seulement 50% des 189 arbres où il était "out of bag", et en versicolor dans les 50% de cas restants.
Ainsi, pour identifier les individus qui tendent à poser problème, on peut utiliser la marge. Pour un individu donné, qui appartient à la classe i, on note Pj la proportion de votes pour la classe j. Alors la marge correspond à:
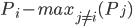
Il s'agit ainsi de la différence entre la proportion de votes pour la classe correcte (i) et la proportion de votes pour la classe sortie majoritaire parmi les autres classes (j ≠ i).
m=margin(iris.rf)
print(m[sous_echant])
## setosa versicolor virginica
## 1.000000000 0.989847716 -0.005291005
Ainsi, plus la marge est proche de 1 et plus la confiance accordée à la prédiction est grande... Au contraire, quand la marge est faible ou même négative, la confiance à accorder à la classification pour l'individu considéré est faible.
Prédiction
La classe prédite est pour chaque individu est, par défaut, celle qui recueille le plus de votes sur l'ensemble des arbres où l'individu est "out of bag".
Voici comment la récupérer sous R
print(iris.rf$predicted[1:10])
## 1 2 3 4 5 6 7 8 9 10
## setosa setosa setosa setosa setosa setosa setosa setosa setosa setosa
## Levels: setosa versicolor virginica
On peut bien évidemment comparer la classe observée et la classe prédite:
table(iris$Species, iris.rf$predicted)
##
## setosa versicolor virginica
## setosa 50 0 0
## versicolor 0 47 3
## virginica 0 4 46
Surprise! on retrouve la matrice de confusion, que l'on peut aussi afficher de la manière suivante:
iris.rf$confusion
## setosa versicolor virginica class.error
## setosa 50 0 0 0.00
## versicolor 0 47 3 0.06
## virginica 0 4 46 0.08
Le taux d'erreur correspond à la proportion de cas où la prédiction est incorrecte:
error_rate=1-sum(diag(iris.rf$confusion))/sum(iris.rf$confusion)
print(error_rate)
## [1] 0.04755561
Il est ici d'environ 5%.
Prédiction sur un nouveau jeu de données
Imaginons maintenant que nous disposions d'un jeu de données dans lequel figurent les descripteurs des individus (longueur et largeur des sépales, longueur et largeur des pétales) mais pas leur espèce. Par exemple, les données disponibles ici
Je peux alors réutiliser ma forêt aléatoire comme classificateur:
predicted=predict(iris.rf,newdata=Species_to_predict)
print(predicted[1:5])
## 1 2 3 4 5
## versicolor virginica virginica virginica virginica
## Levels: setosa versicolor virginica
Importance des variables
L'importance d'une variable dans la classification correspond à la diminution moyenne de l'impureté qu'elle permet. Pour chaque arbre, la diminution totale de l'impureté liée à une variable correspond à la diminution de l'impureté cumulée sur l'ensemble des noeuds qu'elle régit. Cette diminution est ensuite moyennée sur l'ensemble des arbres.
Pour rappel, l'impureté est mesurées par l'index de Gini (cf ce billet sur les arbres décisionnels).
iris.rf$importance
## MeanDecreaseGini
## Sepal.Length 9.714378
## Sepal.Width 2.290949
## Petal.Length 44.439867
## Petal.Width 42.828712
varImpPlot(iris.rf)
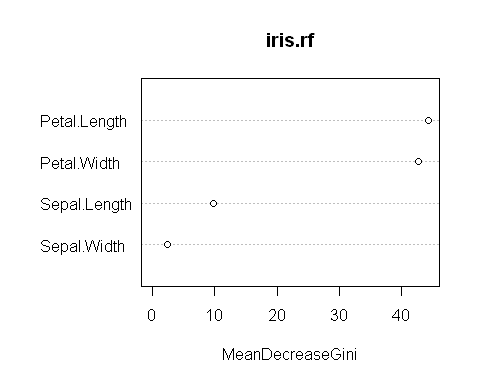
Ici les deux variables qui ont clairement le plus d'importance dans la classification des espèces sont la longueur et la largeur de pétales.
Paramétrisation de la forêt
Dans la construction de chacun des arbres il y a une part d'aléa liée à la fraction du jeu de donnée considérée pour l'entraînement de l'algorithme... Le taux d'erreur observé pour chaque arbre est donc aléatoire. Plus on construit d'arbres, et plus le taux d'erreur "moyen" va converger vers une valeur fixe (ici 5%).
Observons ainsi le taux d'erreur si l'on s'intègre les votes de 1, 2, 3, .... 5000 arbres parmi ceux construits par la fonction randomForest (le nombre d'arbres peut être modifié par le paramètre ntree):
iris.rf=randomForest(iris[,1:4], iris$Species, ntree=5000)
plot(iris.rf$err.rate[,1], type="l")
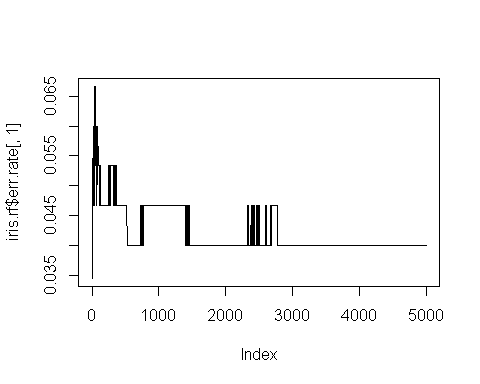
On observe que le taux d'erreur se stabilise autour de 4% (soit 6 erreurs de classement sur 150 individus) quand le nombre d'arbres atteint 3000 environ. Mais en produisant une forêt qui ne compte "que" 500 arbres, on a un taux d'erreur qui tourne autour de 6/150 avec parfois un "bond" à 7/150 donc ce n'est pas non plus l'horreur...
On peut également évaluer (entre autres) l'effet du paramètre sampsize qui fixe la taille de l'échantillon "in bag", ou encore l'effet du paramètre maxnodes, qui limite le nombre de noeuds de chaque arbre:
iris.rf2=randomForest(iris[,1:4], iris$Species, sampsize=140)
iris.rf3=randomForest(iris[,1:4], iris$Species, maxnodes=5)
Les valeur des paramètres sont fixées par défaut d'une manière qui permet "raisonnablement"" d'espérer atteindre la convergence pour 500 arbres... mais rien n'empêche de s'en assurer, empiriquement, à travers le genre de graphique présenté ci-dessus...
Pour une discussion plus approfondie de ces paramètres, rendez-vous sur la page d'aide de la fonction randomForest, ou bien allez voir l'article de Liaw and Wiener (2002)!
Références
Liaw, Andy, and Matthew Wiener. 2002. “Classification and Regression by randomForest.” R News 2 (3): 18–22. http://CRAN.R-project.org/doc/Rnews/.
15 Comments
Mehdi
Super billet ! On comprends bien et on peut refaire la même chose à la maison avec d'autres données... Vraiment super
Synyster
100 fois mieux que le cours de notre prof principal qui , en passant , était à la tête de la Société Française de Statistique ....
Arnaud
Merci pour cet article très clair et très bien vulgarisé
lvaudor
🙂 Merci!
Blum
Bonjour Lise, je viens de découvrir ton blog qui est très plaisant à lire. J'ai 1 petite question à propos de ton post au sujet de l'out of bag error. Quand tu écris
"la forêt aléatoire a classé le 1er individu en "setosa" (donc correctement) dans 100% des 185 arbres où il était "out of bag"",
est-ce que tu entends
"Pour chacun des 185 arbres où l'individu est out-of-bag, le résultat de la classification est correcte"?
Je ne sais pas si ma question est très claire. Michael
lvaudor
Bonjour Michael,
Merci 🙂
Oui effectivement, tu as bien compris!
DEVOS
très clair, très didactique, nettement plus clair que mon professeur agrégé de statistique ...
Merci
Paul
Merci encore pour cet article très didactique que je découvre ce jour!
Etienne
Bonjour et merci pour votre blog.
La procédure change-t-elle pour une variable d'intérêt quantitative ?
lvaudor
Bonjour,
En terme de lignes de commande, la procédure ne change pas... Si la variable réponse est quantitative, la méthode employée par la fonction randomForest() sera (implicitement) une régression plutôt qu'une classification...
Lionel
Bonjour Lise,
En rebouclant avec https://www.quora.com/How-does-random-forest-work-for-regression-1, le principe du vote majoritaire que tu expliques reste donc valable pour une variable cible quantitative ?
Comment s'assurer alors du paramétrage de l'apprentissage de façon à obtenir la meilleure résolution (granularité) du modèle sur la variable cible ? Quelle est la forme de l'erreur avec ce genre de méthode ?
Joshua
Bonjour,
Merci pour votre blog que je viens découvrir et qui est très clair.
Je suis tout nouveau dans R et dans la randomForest et j'essaye d'appliquer la fonction randomForest à des expressions de gènes pour savoir l'expression de quels gènes permet le mieux de discriminer les individus sains des individus malades.
Je lance le script comme décrit dans votre article, tout marche parfaitement. Mais si je le relance une autre fois ce ne sont pas les mêmes gènes qui vont le mieux expliquer la classification sain/malade.
Je voulais savoir pourquoi (est-ce à cause du choix des in bag et des out of bag ?) et est-ce qu'il est possible de déterminer les gènes, les variables qui permettent le mieux la classification sain/malade en prenant en compte tous mes individus ?
Je ne sais pas si je suis très clair
Merci d'avance
aait
Merci beaucoup pour la clarté de l'exposé et svp si les questions posées pourraient trouver réponses cela nous arrangerait beaucoup plus.
Et encore merci !!!
SANOU OURY
MERCI POUR VOTRE TALENT PEDAGOGIQUE TRES REMARQUABLE
Rac
Excellent billet ! Merci