
Comprendre le théorème pour comprendre les modèles bayésiens
Les modèles bayésiens viennent de faire une entrée subite et fracassante dans ma vie. Cela peut sembler étonnant car cela fait maintenant quelques années que le paradigme bayésien connaît un grand succès chez (notamment) les écologues, peut-être du fait des problèmes qu'ils connaissent avec les modèles inférentiels plus classiques (problèmes liés aux données manquantes ou trop peu nombreuses, aux distributions non gaussiennes, aux difficultés d'ajustement des modèles, à l'importance des erreurs, etc.).
Avec ce billet sur le théorème de Bayes, je souhaite entamer une série de billets relatifs aux modèles bayésiens. J'aimerais notamment expliquer leur principe, montrer leurs avantages et inconvénients, et montrer (aussi succintement que possible) comment les construire, les ajuster, et les interpréter sous R.
Pour commencer, je vais me concentrer sur ce qui définit les modèles bayésiens, à savoir (comme leur nom l'indique), leur utilisation des probabilités et notamment du théorème de Bayes...
Le théorème de Bayes, en équation
Le théorème de Bayes est le suivant:
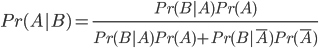
Il exprime la probabilité de "A sachant B" en fonction des probabilités de "B sachant A" et de la probabilité de A.
Il dérive de cette définition des probas conditionnelles:
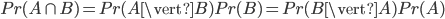
Un exemple concret d'application du théorème
Imaginons un cas concret d'utilisation de ce théorème. Mettons, par exemple, que l'on essaie de comprendre le comportement des ours à travers le modèle suivant, où 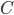 est la variable indicatrice de l'évènement "L'ours est en colère" (
est la variable indicatrice de l'évènement "L'ours est en colère" (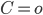 ou
ou 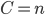 ) et
) et 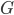 est la variable indicatrice de l'événement "L'ours grogne" (
est la variable indicatrice de l'événement "L'ours grogne" (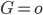 ou
ou 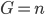 ).
).
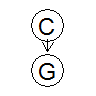
Supposons que l'on connaît la relation qui lie C à G -i.e. la table des probabilités conditionnelles qui donne 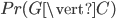 -. Par exemple
-. Par exemple
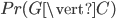 |
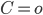 |
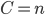 |
|---|---|---|
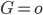 |
0.90 | 0.25 |
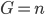 |
0.10 | 0.75 |
On peut lire cette table de la manière suivante:
- la probabilité que l'ours grogne sachant qu'il est en colère est de 90%.
- la probabilité que l'ours grogne sachant qu'il n'est pas en colère est de 25%. Ainsi, il arrive que les ours grognent même s'ils ne sont pas en colère.
Comment, dans ces conditions où les ours grognent à qui mieux mieux, interpréter leurs grognements?
Mettons que l'on suppose a priori que l'ours a une chance sur trois d'être en colère: -i.e. on a l'a priori suivant sur 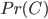 -:
-:
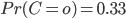
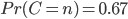
Imaginons que nous observions l'ours une fois, et qu'il grogne.
Alors le théorème de Bayes va nous permettre de déterminer quelles sont les probabilités que l'ours soit en colère (ou non) sachant qu'il a grogné.
En effet:
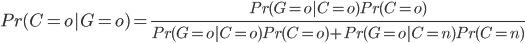
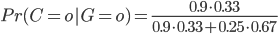
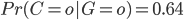
donc, l'ours ayant grogné, on estime la probabilité qu'il ait été en colère à 64%.
Premier aperçu du paradigme bayésien
Quelques remarques, maintenant, quant aux principes qui sous-tendent l'utilisation du théorème de Bayes...
Remarquez d'abord comme le résultat (probabiliste) du modèle permet de retranscrire efficacement les incertitudes. En effet, on ne conclut pas de ce modèle "l'ours a grogné donc il devait être en colère" mais "l'ours a grogné donc la probabilité qu'il ait été en colère est de 64%". L'incertitude est ici intégrée (plutôt qu'associée, comme dans la statistique inférentielle plus classique) au résultat.
Ainsi, en prenant en compte notre observation de G nous sommes passé d'une probabilité a priori 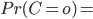 33% à la probabilité a posteriori
33% à la probabilité a posteriori 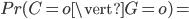 64%. Ainsi, le modèle nous a permis d'affiner notre connaissance de la distribution de C. On pensait a priori que l'ours n'était pas si colérique que ça, mais notre observation de son grognement nous pousse à revoir un peu notre jugement...
64%. Ainsi, le modèle nous a permis d'affiner notre connaissance de la distribution de C. On pensait a priori que l'ours n'était pas si colérique que ça, mais notre observation de son grognement nous pousse à revoir un peu notre jugement...
Si l'on était partis d'un a priori différent (par exemple 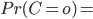 90%), la distribution a posteriori aurait été différente (ici
90%), la distribution a posteriori aurait été différente (ici 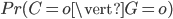 = 99%). L'a priori a donc un effet non négligeable sur la distribution a posteriori et il convient de le définir avec soin. En pratique, néanmoins, on utilise souvent les modèles bayésiens en se basant sur de nombreuses observations (et non une seule comme nous l'avons fait plus haut)... Or plus les observations sont nombreuses, moins l'effet de l'a priori de départ se ressent sur la distribution a posteriori.
= 99%). L'a priori a donc un effet non négligeable sur la distribution a posteriori et il convient de le définir avec soin. En pratique, néanmoins, on utilise souvent les modèles bayésiens en se basant sur de nombreuses observations (et non une seule comme nous l'avons fait plus haut)... Or plus les observations sont nombreuses, moins l'effet de l'a priori de départ se ressent sur la distribution a posteriori.
30 Comments
Jean-Pierre MALICIEUX-GAUTIEZ
Simplement génial comme explication. Bravo et Merci.
lvaudor
Merci 🙂
damien s
Bonjour, je crois qu'une erreur c'est glissée dans le calcul du grognement d'ours !
La probabilité qu'il soit en colère après un grognement est plutôt de 64 % non ?
0,9*0,33 = 0,297
0,25*0,67 = 0,1675
0,297/(0,297+0,1675) = 0,64
lvaudor
Vous avez tout à fait raison! J'ai corrigé l'erreur dans l'article... Merci!
issac n'ti Achampong
C'est très bien bravo et merci
Simon
Cela fait maintenant longtemps que je suis votre blog et il est simplement génial ! Merci beaucoup pour l'ensemble de vos billets.
lvaudor
Merci Simon, cela me fait très plaisir d'avoir de bons retours 🙂
SIMON (un autre)
Merci pour votre Blog mais peut-être n'ai-je pas tout compris ou alors vous avez corrigé l'erreur dans les équations, mais vous ne l'avez pas corrigé dans le corps du texte : 64 ou 82% ? Ou alors je n'ai rien compris :-).
lvaudor
Oui vous avez bien compris! j'avais corrigé l'erreur dans l'équation et non dans le corps du texte... Merci!
SIMON (un autre)
De rien. Comme j'ai bien tout compris 🙂 je peux donc vous dire que je suis entièrement d'accord avec l'autre Simon. On vous lit, on comprend des notions qui ont l'habitude d'être présentées ailleurs de manière totalement absconse ! Merci !
lvaudor
🙂
Alizé
Bonjour, merci pour ces explications très claires et enfin faciles à comprendre!!
Juste une petite question (stupide sans doute mais je m'embrouille les pinceaux), comment est-ce que vous recalculez la probabilité à posteriori Pr(C=o) pour obtenir les 82%? Merci par avance!
lvaudor
C'est parce que j'ai décidément du mal avec ces 82% qui se sont glissés partout dans mon texte!! C'est bien 64% et non 82%. Et cette fois-ci, je crois que j'ai fait la correction VRAIMENT PARTOUT!
faucher
comment connait on les valeurs du premier tableau ?
lvaudor
Le premier tableau, c'est l'un des points de départ du raisonnement. On le connaît d'"emblée". Par exemple je pourrais connaître ce tableau "d'emblée" si j'avais connaissance des résultats d'une expérience préalable, mesurant conjointement
On peut imaginer que la pose d'un casque à électrodes à un ours est une opération délicate et coûteuse donc, une fois qu'"on" (un chercheur assez fou pour tenter cette expérience quelque part dans le monde) a estimé la loi de probabilité des grognements conditionnellement au sentiment de colère, il peut être avantageux de recourir à la méthode bayésienne abordée dans ce billet. En effet, elle permet d'estimer la probabilité qu'un ours soit en colère (sentiment difficile à mesurer directement) en se basant sur son grognement, qui, lui, est facile à observer...
Houbaut-Vigneron
Bonjour,
Super explication, claire et précise.
je relève juste une petite erreur, vous marquez
"Mettons que l'on suppose a priori que l'ours a une chance sur trois d'être en colère: -i.e. on a l'a priori suivant sur Pr(C)-:
Pr(C=o)=0.33
Pr(C=n)=0.66"
Si on prend l'équation et le résultat qui est juste vis-à-vis de cette dernière, Pr(C=n) doit être égal à 0.67
Ce qui serait juste par rapport a Pr(C=o)=0.33, 1-0.33=0.67
Encore bravo pour l'article.
lvaudor
En effet!! Erreur d'arrondi...
Merci!
Pierre
Merci mille fois pour cet article très éclairant pour un simple juriste que je suis !!!
Clara
Bonjour! Merci pour cet article! Vraiment très bien expliqué!
J'ai une petite question : Vous écrivez à la fin de votre article : "Ainsi, en prenant en compte notre observation de G nous sommes passé d'une probabilité a priori Pr(C=o)= 33% à la probabilité a posteriori Pr(C=o)= 64%."
Mais ce n'est pas Pr(C=o/G=o) qui vaut 64%?
lvaudor
Oui effectivement. Je m'étais relâchée sur la notation parce que je mentionnais "a priori"/"a posteriori" dans le texte. J'ai remis la notation stricte pour plus de clarté... Merci!
Manu
Merci pour cet article !
Quelque chose m'échappe sur l'affirmation de votre dernière phrase.
Pourquoi "plus les observations sont nombreuses, moins l'effet de l'a priori de départ se ressent sur la distribution a posteriori." ?
En imaginant que le tableau de contingence de départ soit basé sur 50 observations et puis qu'on a exactement le même avec 5000000 observation... je ne vois l'impact...
lvaudor
Bonjour,
Alors, effectivement, on suppose que le tableau des probabilités conditionnelles ne change pas en fonction de l'effectif (ça ne fait pas partie des inconnues: on suppose qu'on connaît très exactement la proba que l'ours grogne s'il est en colère). Par contre, imaginons que je parte d'un a priori qui est celui-ci: "Les ours passent 80% de leur temps à être en colère". Si j'observe 3 ours et que les 3 ne grognent pas (soit 100%), cela va à l'encontre de mon a priori et pourtant mon estimation a posteriori de la "colère intrinsèque" des ours n'est pas tellement modifiée car je manque de "preuves" pour aller à l'encontre de mon estimation a priori... Si j'observe 1000 ours et que 997 (soit 99.7%) ne grognent pas, par contre, cela aura un impact important sur mon estimation a posteriori (je conclurai vraisemblablement que finalement les ours ne passent pas tant de temps que ça à être en colère...).
Zahir AITMATEN
En fin j'ai trouvé quelqu'un qui m'explique vraiment le théorème de Bayes. j'ai fait le tour du WEB pour cela et me voila enfin arrivé au bon endroit. je vous remercie infiniment monsieur pour votre contribution qui m'a aidé et qui peut aider des milliers voir des millions de gens qui tombe dessus. thanks lot
Guillaume Le Lay
Merci pour l'article, clair tout en restant concis ! Bravo
lvaudor
🙂
Céline-Christelle COTTET
Super clair !
Jean
Bonjour,
J'essaye, en vain de résoudre ceci à l'aide de Bayes.
Si vous voulez m'aider SVP ?
Le vaccin imaginaire V contre la maladie M tout aussi imaginaire est efficace à p%.
On pose arbitrairement par p=0.
70% d'une population de plusieurs millions est vaccinée et 30% ne l'est pas.
1000 individus tombent malades.
Sur les 1000, 220 auront été vaccinés.
La maladie M s'évite par des gestes G qui sont efficaces à 100%.
Parmi les malades, aucun n'aura effectué les gestes G.
Le vaccinés ont une propention x fois plus grande que les non vaccinés à effectuer les gestes G.
Quelle est la valeur de x ?
Maintenant on prend p = 60%. Quelle est la valeur de x ?
Quelle est la fonction mathématique qui permet de calculer x en fonction de p?
Est-ce que l'intuition que l'on peut avoir p=0 avec x>5 est bonnes?
Autrement dit, 22% de malades vaccinés, des non vaccinés 6 fois moins respectueux des et une efficacité à 0% est-elle possible ?
Cordialement,
Jean
Jean
Bonjour,
Je pense avoir compris.
On met 60 millions de boules dans un sac.
Sur les 60 millions, 72% des boules sont vertes et les boules restantes sont oranges.
Sur les 10 millions de boules, 10 000 sont marquées d'un point rouge et les boules restantes d'un point blanc.
Parmi ces 10 000 boules marquées d'un point rouge, on compte 4 fois plus de boules vertes que d'orange.
On effectue un tirage, boule après boule.
Lorsque l'on rencontre une boule marquée en rouge on la conserve.
Ceci jusqu'à arrivé à 10 000 boules marquées d'un point rouge.
Alors on constate que 20 % des boules sont vertes et 80 % sont orange (on compte 4 fois plus de boules vertes que d'orange parmi les 10 000)
verte = V = vacciné (il s'agit d'un vaccin imaginaire)
orange = non vacciné
rouge = malade = applique toujours les gestes barrières (il sagit d'une maladie imaginaire et de gestes barièe imaginaires)
blanc = non malade = n'applique pas toujours les gestes barrières
Avec un pourcentage de boule verte parmi les 60 millions variant de 0 à 100% , on obtient toujours le même résultat: on constate après tirage que 20 % des boules sont vertes et 80 % sont orange.
Dans l'idée que les vaccinés sont 4 fois moins malade parce qu'ils sont 4 fois plus nombreux (en proportion) à appliquer toujours les gestes barrières.
Autrement dit, l'efficacité du vaccin imaginaire serait nulle?
Il ne s'agirait ni de probabilité, ni de Bayes mais d'un décompte?
Cordialement,
Jean
Jean
Erratum:
on compte 4 fois moins de boules vertes que d'orange parmi les 10 000
et non pas
on compte 4 fois plus de boules vertes que d'orange parmi les 10 000
Ibn El Farouk
Une problématique, une modélisation et une explication limpides. Mes connaissances augmentent à propos des probabilités des causes. Tout mon respect et reconnaissance sincère.