Réseaux et graphes: pour quoi faire?

Un graphe est un ensemble de points (ou sommets, ou noeuds, ou vertices en anglais) qui peuvent être reliés deux à deux à deux par un ou plusieurs liens (ou arêtes, ou arcs, ou edges en anglais).

Voilà une définition on ne peut plus générale (et donc une méthode on ne peut plus généraliste!!).

On peut en effet représenter par un graphe un grand nombre de types de données relatives à des "réseaux" (liens, influences, partages, citations, échanges) etc....

Les réseaux sociaux sont ainsi un exemple "grand public" d'application des graphes. Par un graphe, en effet, on peut représenter qui est ami de qui (version Facebook), ou qui est follower de qui (version Twitter et ResearchGate), quelle est la distance qui sépare un individu d'un autre (en terme de nombre de liens par exemple), s'il y a des "communautés" où la densité de liens est particulièrement forte, etc....

Une autre application extrêmement usuelle des graphes est la bibliométrie, ou la textométrie. Dans ce cas on s'applique, par exemple, à représenter des liens ou influences entre des auteurs, ou des liens entre articles ou revues, sur le mode "qui cite qui".

Exemple

Considérons le jeu de données suivant, comprenant une table relative aux liens et aux noeuds du réseau:

table_edges=read.table(paste(dat.path,"edges.csv",sep=""),
                         sep=";", header=T)
table_vertices=read.table(paste(dat.path,"vertices.csv",sep=""),
                         sep=";", header=T)
head(table_edges)

##    Source   Target Weight   Label
## 1 Sabrina    Cindy      2 friends
## 2   Greta     Gina      2 friends
## 3    Gina Fredrick      1  couple
## 4   Greta    Björn      1  couple
## 5   Julia  Juliano      1  couple
## 6   Julia    Greta      2 friends

attach(table_edges)
head(table_vertices)

##         Id    Label  Type
## 1   Audrey   Audrey woman
## 2  Beverly  Beverly woman
## 3    Björn    Björn   man
## 4  Caitlin  Caitlin woman
## 5 Caitlin  Caitlin  woman
## 6    Caleb    Caleb   man

attach(table_vertices)

Ce jeu de données décrit les relations unissant 35 personnes. Sabrina est amie avec Cindy, Greta est amie avec Gina, Gina est en couple avec Fredrick, etc.

Je vais utiliser le package igraph pour représenter les liens entre toutes ces personnes.

require(igraph)

Je réalise un graphe non-orienté. C'est-à-dire que je suppose que les liens entre les personnes sont symétriques (si une personne x est amie avec une personne y, alors y est amie avec x...)

par(mar=c(0,0,0,0))
g=graph.data.frame(table_edges, directed=FALSE)
graph_layout=layout.fruchterman.reingold(g)
plot(g,layout=graph_layout)

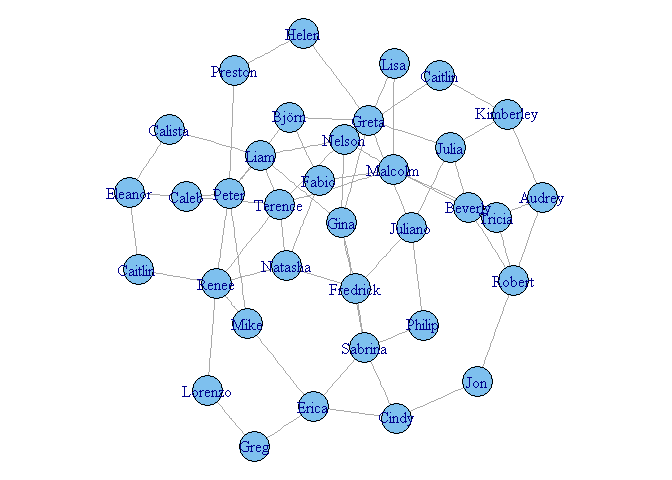
Grâce aux deux lignes de commande ci-dessus, j'obtiens un beau(?) graphe.

(Je ne sais pas pour vous mais moi je trouve ça trop magique!... même si en l'occurence, dans cet exemple c'est un "petit" graphe de rien du tout)

Je peux modifier son apparence, par exemple en faisant en sorte que Gina soit mise en avant dans le graphe:

par(mar=c(0,0,0,0))
V(g)

## Vertex sequence:
##  [1] "Sabrina"   "Greta"     "Gina"      "Julia"     "Juliano"   "Helen"     "Calista"   "Fabio"     "Audrey"    "Malcolm"   "Lisa"      "Cindy"     "Peter"     "Nelson"    "Terence"   "Greg"      "Eleanor"   "Caitlin"   "Natasha"   "Caleb"     "Robert"    "Tricia"    "Lorenzo"   "Renee"     "Beverly"   "Björn"     "Jon"       "Mike"      "Fredrick"  "Philip"    "Liam"      "Preston"   "Kimberley" "Erica"     "Caitlin "

plot(g,layout=graph_layout, mark.group=3)

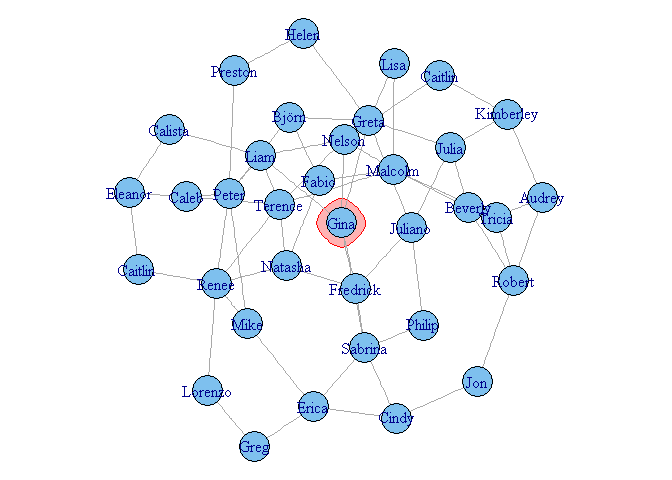
Je peux aussi modifier l'apparence des arêtes (edges), par exemple pour que le lien soit le plus épais pour les couples (Weight=3), le moins épais pour les collègues de travail (Weight=1) et intermédiaire pour les amis (Weight=2):

par(mar=c(0,0,0,0))
plot(g,layout=graph_layout,edge.width=Weight)

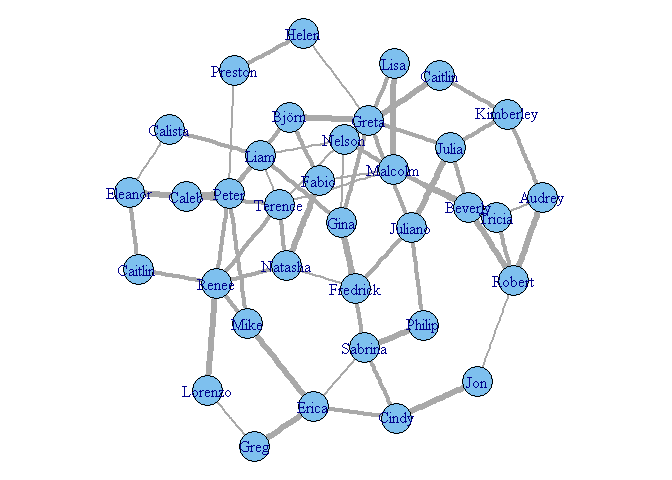
Méthode de tracé des graphes

Une autre manière (plus "profonde") de modifier l'apparence du graphe est de modifier l'algorithme de tracé. La manière adéquate pour tracer de "beaux" graphes bien clairs a fait l'objet d'une littérature assez importante (et assez ancienne!) : voir par exemple Reingold, John, and Tilford (1981), Kamada and Kawai (1989), Fruchterman and Reingold (1991).

En pratique, voilà comment modifier la méthode de tracé avec le package igraph:

layout(matrix(1:4,nrow=2))
par(mar=c(0,0,2,0))
plot(g, layout=layout.circle,main="Circle")
plot(g, layout=layout.fruchterman.reingold,main="Fructerman-Reingold")
plot(g, layout=layout.reingold.tilford,main="Reingold-Tilford")
plot(g, layout=layout.kamada.kawai,main="Kamada-Kawai")

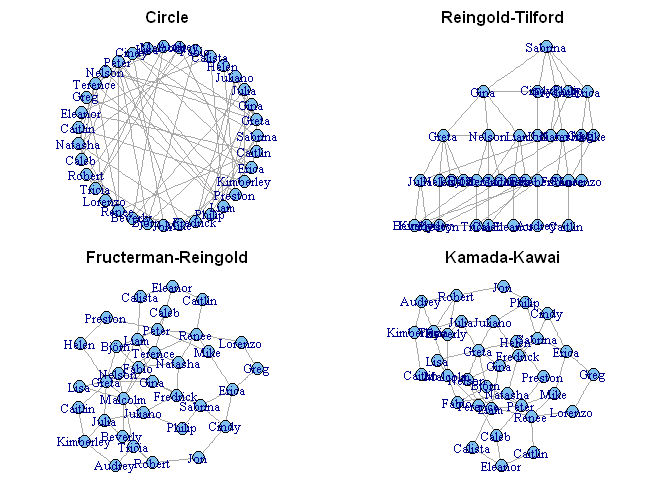
Notez que si les graphiques ci-dessus sont réalisés à l'aide d'une fonction graphique "classique", vous pouvez aussi créer un graphe interactif (qui vous permet, entre autres, de modifier l'apparence et l'emplacement des vertices et des liens "à la main") avec la fonction suivante:

tkplot(g,layout=graph_layout)

Pour aller plus loin

Je n'ai présenté ici que le "minimum vital" pour réaliser un graphe sous R... Pour en savoir plus sur le package igraph vous pouvez vous rendre sur le site qui lui est consacré.

Enfin, si la construction de graphes vous intéresse particulièrement mais que vous n'êtes pas très à l'aise avec R, je vous invite à prendre connaissance du logiciel Gephi, un logiciel libre permettant d'analyser et visualiser les réseaux de manière assez conviviale.

Références

Fruchterman, Thomas M. J., and Edward M. Reingold. 1991. “Graph Drawing by Force-Directed Placement.” Software: Practice and Experience 21 (11): 1129–64. doi:10.1002/spe.4380211102. http://doi.wiley.com/10.1002/spe.4380211102.

Kamada, Tomihisa, and Satoru Kawai. 1989. “An Algorithm for Drawing General Undirected Graphs.” Information Processing Letters 31 (1): 7–15. doi:10.1016/0020-0190(89)90102-6. http://linkinghub.elsevier.com/retrieve/pii/0020019089901026.

Reingold, Edward M., John, and S. Tilford. 1981. “Tidier Drawing of Trees.” IEEE Trans. Software Eng.