
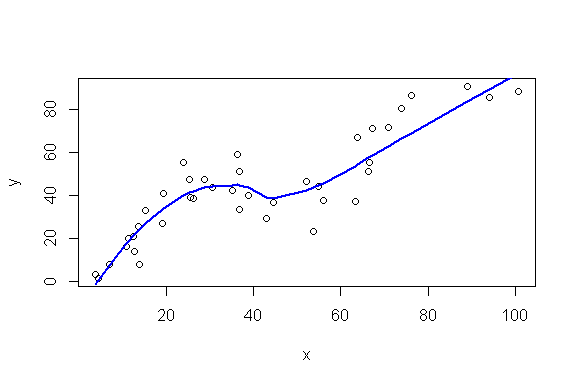
La régression loess (ou "lowess") est une méthode de régression non-paramétrique (c'est-à-dire qu'elle n'est pas associée à une équation, comme par exemple une régression linéaire ou polynomiale classique). Elle permet de produire des courbes lissées, ajustées à un nuage de point, un peu comme ici, par exemple:
Mise en oeuvre
Considérons le jeu de données data.csv:
data=read.table(paste(dat.path,"data.csv",sep=""),sep=";",header=T)
attach(data)
Pour ajuster une régression loess, rien de plus simple... Il suffit de faire appel à la fonction ... loess.
mod=loess(y~x)
print(mod)
## Call:
## loess(formula = y ~ x)
##
## Number of Observations: 40
## Equivalent Number of Parameters: 4.4
## Residual Standard Error: 9.486
On récupère les coordonnées des points de la courbe de la manière suivante:
yfit=predict(mod, newdata=x)
On peut alors représenter le nuage de points et la courbe loess:
plot(x,y)
lines(x,yfit, col="blue",lty=3, lwd=2)
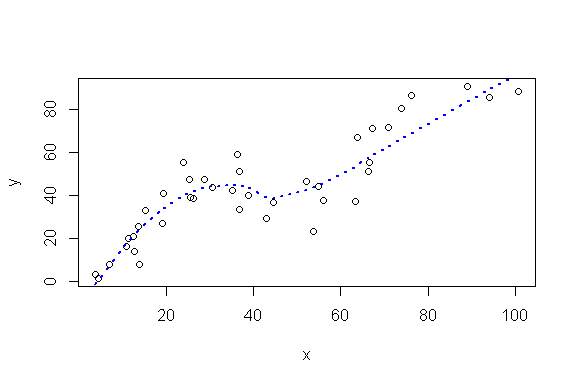
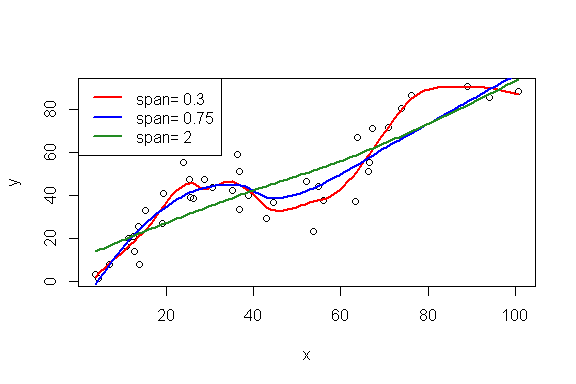
En modifiant le paramètre span de la fonction loess, on peut produire des courbes plus ou moins lissées:
mod1=loess(y~x,span=0.3)
mod2=loess(y~x,span=0.75)
mod3=loess(y~x,span=2)
xfit=seq(from=min(x),to=max(x),length.out=100)
yfit1=predict(mod1,newdata=xfit)
yfit2=predict(mod2,newdata=xfit)
yfit3=predict(mod3,newdata=xfit)
plot(x,y)
points(xfit,yfit1,type="l",lwd=2,col="red")
points(xfit,yfit2,type="l",lwd=2,col="blue")
points(xfit,yfit3,type="l",lwd=2,col="forestgreen")
legend("topleft",c(paste("span=",c(0.3,0.75,2))), lwd=2,lty=1, col=c("red","blue","forestgreen"))
Principe
Dans une régression loess, l'ajustement de la courbe se fait localement. Pour déterminer la valeur y que prend la courbe au point d'abscisse xi, on ajuste un polynôme de degré 1 ou 2 aux points au voisinage de xi. Cet ajustement se fait avec pondération: les points les plus proches de xi ont davantage de poids dans l'ajustement.
Voisinage:
La taille du voisinage est déterminée par un paramètre α. Quand
Les points dans le voisinage d'un xi donné sont représentés en rouge dans l'animation ci-dessus. La fonction loess appelle ce paramètre α span, et par défaut span=0.75.
Quand α ≥ 1, tous les points sont utilisés. L'ajustement ne dépend alors plus de α à travers la détermination du voisinage. En revanche α joue toujours sur le calcul des poids (cf ci-après).
Pondération:
Le poids ρ d'un point d'abscisse xj au voisinage de xi est d'autant plus important que sa distance
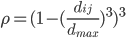
Quand
Quand ,
Ajustement:
Une fois le voisinage et les poids déterminés, une courbe correspondant à un polynôme de degré 1 ou 2 est ajustée pour une série de valeurs xi (ici c'est un polynôme de degré 2, dont la courbe apparaît en rouge dans l'animation ci-dessus). La valeur prédite en ce point xi par la régression loess correspond à la valeur prédite par le polynôme ajusté localement.
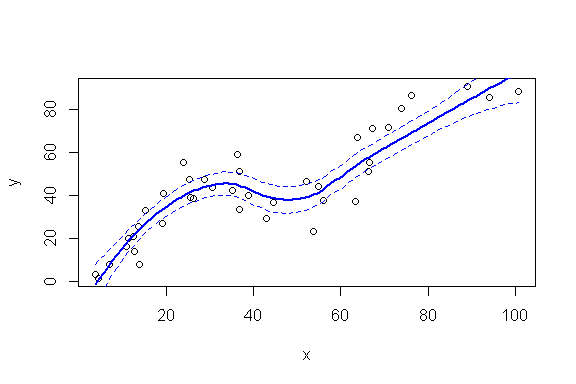
Bandes de confiance autour de la courbe
Le calcul de la courbe ajustée peut-être assorti d'une mesure de l'erreur standard:
xfit=seq(from=min(x),to=max(x),length.out=100)
prediction=predict(mod,newdata=xfit, se=TRUE)
yfit=prediction$fit
yfit_se=prediction$se
print(yfit_se[1:5])
## [1] 4.754606 4.354402 3.987376 3.654491 3.356802
On peut ainsi utiliser cette erreur standard pour calculer une bande de confiance (ici à 95%):
plot(x,y)
points(xfit,yfit, col="blue",type="l", lwd=2)
points(xfit,yfit+1.96*yfit_se, col="blue",type="l", lwd=1, lty=2)
points(xfit,yfit-1.96*yfit_se, col="blue",type="l", lwd=1, lty=2)
15 Comments
Amélie
Lise, ton blog vient de me sauver la vie... Merci !
(et joyeux tout ça tout ça... 😉 )
lvaudor
Coucou Amélie! Merci merci! Et contente de t'avoir sauvé la vie... 🙂
Josephine
Bonjour, j'ai bien aime ton blog.
Je travaille ma these en ce temps la, et je suis en train de decouvrir la methode de Loess.
Ton blog m'a bien aide.
Est ce que vous pouvez me dire comment vous avez pu realiser le video?
C'est tres interessant!
Difah
intéressant !!!!
Mathematicsman
Bonjour,
C'est très intéressant et très clair. Quelles sont tes sources?
Je te remercie par avance.
Mathematics man
lvaudor
Bonjour Mathematics man, et merci!
Eh bien, ma source principale est le fichier d'aide associé à la fonction "loess"!... Tout simplement! 🙂
Jacques
Bonjour,
Merci pour cet article qui est très agréable !
Etes vous d'accord pour dire que la méthode LOESS ne peut être prédictive pour des points n'appartenant pas à l'échantillon et sur les bords (par exemple si x=110) ?
lvaudor
Bonjour,
Merci pour votre commentaire. Effectivement, pour un point sur les bords (i.e. n'appartenant pas à la gamme de valeurs utilisées pour ajuster la régression) on ne peut pas utiliser la méthode prédictivement (ou du moins, on peut mais on ne devrait pas). En revanche, dans le cas contraire on peut prédire une valeur pour un point n'appartenant pas à l'échantillon (c'est une prédiction très "empirique" mais une prédiction tout de même). (Je ne suis pas sûre d'avoir bien compris votre question mais je vais tenter cette réponse 😉 )
Jacques
Oui c'était bien cela, merci pour la confirmation !
r2d2
Bonjour Lise, ton blog est super, merci ! Pour la régression loess, je rencontre un problème avec l'ajustement qui donne des valeurs supérieures à 100% à certains endroits des courbes. S'agissant de taux d'activité, c'est un peu problématique ! J'imagine que c'est le calcul de l'ajustement qui produit ça mais y-a-t'il une façon de procéder pour l'éviter ? Merci beaucoup !
lvaudor
Merci 🙂
Alors, eh bien je crois que l'idée de faire de la "constrained loess regression" (c'est ce que j'ai googlé pour avoir des pistes ;-)). J'ai par exemple trouvé ce thread sur StackOverflow. Ils parlent plus particulièrement de la réalisation graphique de la régression via ggplot avec geom/stat_smooth (chose qu'il faudra que j'aborde d'ailleurs en éditant ce billet!) mais le fond du problème est le même. Leur problématique est cependant un tout petit peu différente car ils ne veulent pas de valeurs <0 (donc la suggestion de passer par une transformation exp/log n'est pas correcte pour ton cas: il faudrait passer par une transformation logit/inverse logit j'imagine).
Julien
Bonjour,
Comment est calculé la valeur d'une nouvelle donnée test ? Autrement dit quel polynôme est choisi parmi tous les polynômes ajustés ? Je pense que l'on choisit la donnée d'entraînement qui a la plus petite distance à la donnée test et on prend le polynôme correspondant à cette donnée d'entraînement. Est-ce bien cela ? Merci
lvaudor
Bonjour,
Eh bien en fait, si j'ai bien compris la question: pour une nouvelle donnée test, un nouveau polynôme est ajusté, avec les points au voisinage de cette nouvelle donnée (il n'y a pas autant de polynômes qu'il y a de données "anciennes", il y a autant de polynômes qu'il y a de données "nouvelles")...
Nath
Bonjour et merci pour l'article très clair !
Je me demandais s'il était possible de retrouver une approximation de la fonction d'estimation si celle-ci parait vaguement linéaire ??
Merci !
Julien
La phrase suivante n'est pas très claire :
", une courbe correspondant à un polynôme de degré 1 ou 2 est ajustée pour une série de valeurs xi"
Est-ce qu'un polynôme différent est ajusté pour chaque xi (différent) ?