During a talk about his article [Gra1] in Oberwolfach,
D.W. Masser asked F. Gramain the following question : are
the entire functions ![]() solutions of the difference equations system
solutions of the difference equations system
| |
(1) |
In a first article [BéGra1], J.-P. Bézivin and F. Gramain
gave a negative answer to this question
considering the example of the function ![]() , and
showed that if
, and
showed that if ![]() belongs to
belongs to ![]() and if the coefficients of one of the two equations are constant, then
and if the coefficients of one of the two equations are constant, then
![]() is an exponential polynomial.
Moreover, they proved, still assuming
that
is an exponential polynomial.
Moreover, they proved, still assuming
that ![]() belongs to
belongs to ![]() , a serie of partial results
that allowed us to conjecture that every entire solution of a system
with polynomial coefficients is the quotient of an exponential
polynomial by a polynomial. This conjecture has been proved with
other results in a second article [BéGra2] :
, a serie of partial results
that allowed us to conjecture that every entire solution of a system
with polynomial coefficients is the quotient of an exponential
polynomial by a polynomial. This conjecture has been proved with
other results in a second article [BéGra2] :
Théorème [J.-P. Bézivin- F. Gramain]
Let ![]() an entire function entière solution
of the system (1)
then
an entire function entière solution
of the system (1)
then ![]() is the quotient of an exponential
polynomial by a polynomial.
is the quotient of an exponential
polynomial by a polynomial.
In fact, we can replace the right members of (1) by exponential
polynomials. We only have to notice, as in the "Lemme 2.5" of
[BéGra1], that for every complex
number ![]() and for every exponential
polynomial
and for every exponential
polynomial ![]() , there exists a finite relation of linear
dépendence
over
, there exists a finite relation of linear
dépendence
over
![]() between the shifts of
between the shifts of ![]() by
by ![]() (we say that
(we say that ![]() is a recurrent step for the entire function
is a recurrent step for the entire function ![]() -it is a definition due to D. Masser).
-it is a definition due to D. Masser).
In the last part of [BriHab], we present an algorithm that allows to determine the entire solutions of the systèm (1).
Moreover, J.-P. Bézivin and F. Gramain proved in
[BéGra2] that if we replace, in the
second equation of (1), the shifts of ![]() by
by ![]() by
derivatives of
by
derivatives of ![]() , an entire solution
, an entire solution
![]() is still
the quotient of an exponential
polynomial by a polynomial.
The algorithm slightly modified allows again to determine the entire
solutions
is still
the quotient of an exponential
polynomial by a polynomial.
The algorithm slightly modified allows again to determine the entire
solutions ![]() of the system.
of the system.
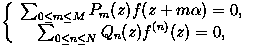 |
(2) |