Washboard Road
The Dynamics of Granular Ripples Formed by Rolling Wheels

This work is a collaboration between Nicolas Taberlet, Stephen Morris and Jim McElwaine
with the help on Anne-Florence Bitbol, done at the DAMTP, University of Cambridge.

It was published in Physical Review Letters, 99, 068003 (2007) 
_______________________________________________________________

washboard Road
Picture by David C. Mays, Complexity, 5, 51 (2000)
     
What is a washboard road?
When a car rides on an unpaved road (made of sand or gravel for instance) a wavy pattern develops. Initially, tiny ripples appear periodically (i.e. roughly equally spaced) and then grow bigger and bigger as cars pass on the road.

This phenomenon known as washboard road is not only extremely aggravating for the drivers but also represents a real danger since the adherence on the road is considerably reduced.

Washboard roads exist throughout the world but they particularly cause annoyance in Australia and developing countries in Africa.
_______________________________________________________________

Our experimental setup

Washboard roads have been studied by engineers but little is known about the fundamental nature of the  instability. As physicists and mathematicians, we want to use a simplified system to study the underlying mechanisms of washboard formation.

Our experimental setup consists of a rotating table (1 meter or 3 feet in diameter) on which a layer of sand is laid (2 to 4-inch thick). A hard rubber wheel attached to an arm and is free to roll on the granular road. In our experiment, the velocity of the wheel ranges from 0 to 3 m/s (i.e. 10 km/h or 7 mph).

Our system is simpler than a car in many ways:

• there is no suspension
• there is no tire
• the wheel is dragged along the road i.e. no torque is applied by an engine
 • the road is periodic: the same wheel passes on and on on the same spot

     Experimental setup
_______________________________________________________________

Numerical Simulations

We also developed Discrete Element Method (D.E.M.) numerical simulations. The method is also known as Soft-sphere Molecular Dynamics.  In the simulation, the system is two-dimensional and consists of a layer of small disks (up to 50 000) laid on a surface. Just like in our experiment, a wheel (which is free to roll) is dragged at constant velocity on the road. Again, the system is periodic.
DEM simulations
_______________________________________________________________

Results

The first result is that is works!

Rapidly after a few passes of the wheel, washboard waves spontaneously appear on the road, both in our experimental setup and in our 2D numerical simulations (see figure above). On the right are the washboard patterns obtained after one hundred passes of the wheel.

The fact that our simplified systems produce washboard ripples is important since it shows that neither tyres nor suspensions are necessary to obtain washboard roads, although of course, adding a spring, a dashpot, a tyre or an engine would affect the size of the bumps. In other words, it is not because of the suspension of cars that washboard roads exist. The ripple wavelength is NOT simply the speed of the wheel times  the bounce frequency
of the suspension, which seems to be a common  belief.

Another interesting result is that the size of the wheel and the size of the grains has no influence on the pattern. The mass of the wheel does however. If the size of the wheel is doubled while keeping its mass constant, the size and wavelength of the ripples remain unchanged. Similarly, using very fine sand (average size of 200 µm) and coarse grains (3 mm), we obtained an identical pattern.
 washboard on sand
Washboard on coarse grains of sand

washboard on rice
Washboard on long-grain rice

Washboard Road in the lab
Washboard road in slow motion

                                                                               More movies can be seen here.

______________________________________________________________

Robustness of the phenomenon

Using our experimental setup, we were able to obtain washboard roads for wide variety of parameters. Ripples were seen for dry or wet sand, with fine or coarse grains, using long-grain rice or beach sand, with an added spring, for various weights of the wheel and for a large range of speeds. This shows that the phenomenon is very robust (i.e. general). In fact, similar phenomena exist on rail tracks and on ski slopes.

The speed of the wheel appears to be crucial. Indeed, there exists a critical velocity below which the road always remains flat and above which washboard bumps appear. Typically, for a car this critical velocity is around 5 mph or 8 km/h.

______________________________________________________________

Compaction and segregation

When a mixture of grains of different sizes is shaken, for instance, grains of similar sizes tend to gather. This phenomenon can be seen in many situations and is called segregation (by size). In our simulations, we have introduced grains whose diameter ranged from a value d (3 mm) to 1.5 d. In the figure on the right (top), the grains are colored according to their size. The conclusion that can be drawn is that no segregation can be seen. Instead, the grains remain well mixed. This shows that grain segregation is not a crucial ingredient of the formation of washboard roads. If we were to use a wider range of sizes, segregation might appear but it would be peripheral to the phenomenon.

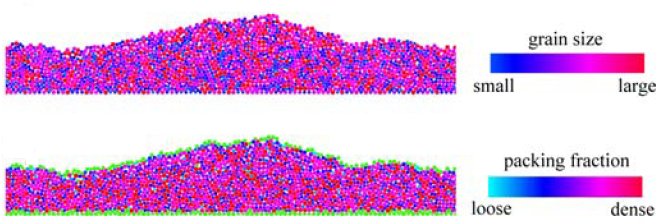   compaction_segregation

Using our numerical simulations we were able to compute the local packing fraction (i.e. how densely packed the road is). On the bottom picture, the grains are colored according to the local packing fraction. Again no general trend is seen, meaning that the compaction within the road is not a key element of washboard formation. 
_______________________________________________________________

Space & Time evolution

As mentioned above, the washboard pattern initially appears as small ripples which later grow bigger and bigger. The amplitude (i.e. height) and wavelength (i.e. distance between consecutive ripples) of the washboard road increase in time with a very interesting dynamic. Due to the periodic nature of our experiment, the wavelength in a steady state is quantized. A consequence of this fact is that a ripple has to disappear for the wavelength to increase. Note that this is still true (but to a lower extent) on a linear (non-periodic) road.
The figure on the right shows the evolution of the vertical amplitude of the wheel motion, both in time and space, starting from a flat road. Merging events (the fusion between ripples) can be seen and display a complex behavior since they involve several ripples. Under other circumstances, namely when the velocity is not kept constant but is gradually decreased, ripple splitting can be observed. One ripple then gives birth to two others.
     
_______________________________________________________________

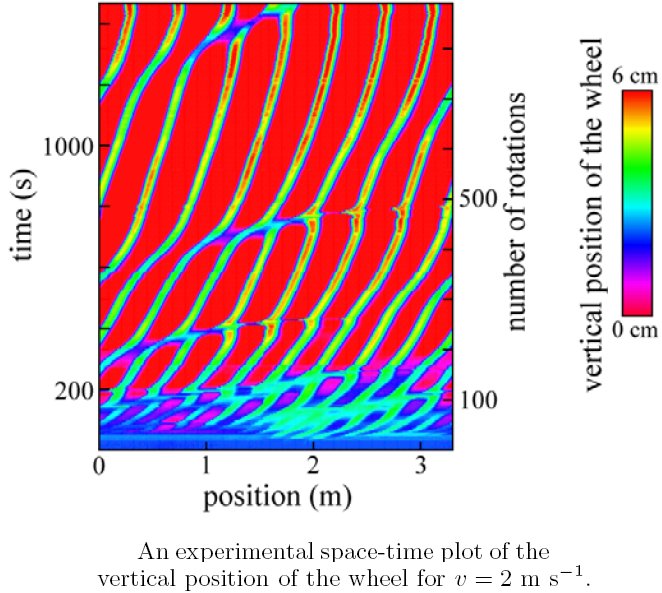Scaling Laws

We have established that washboard roads exist with a simplified system with no suspension or tire. We have also found that the diameter of the wheel and the size of the grains are unimportant to the phenomenon. Finally, washboard patterns were obtained with a blocked wheel (which couldn’t spin), means that the moment of inertia of the wheel is unimportant as well.

Overall, the only relevant parameters are:
• m, the mass of the wheel (per unit of width), in kg.m-1
• ρ, the density of the bed , in kg.m-3
• v, the velocity of the wheel, in m.s-1
• g, the acceleration of gravity, in m.s-2

This allowed for a dimensional analysis which yields one unique dimensionless number which characterizes the washboard instability: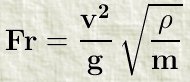


This Froude number gives the scaling laws. For instance, it can be infered that the critical velocity scales as the power 1/4 of the mass.
This idea was tested and validated against the experiment.