temps-fréquenceréallocationinvariance d'échelle
détection
localisation
incertitude
complexité
Empirical Mode Decompositionlongue dépendance et processus stables
cascades
télétrafic
transformation de Lamperti
invariance d'échelle brisée
réallocation
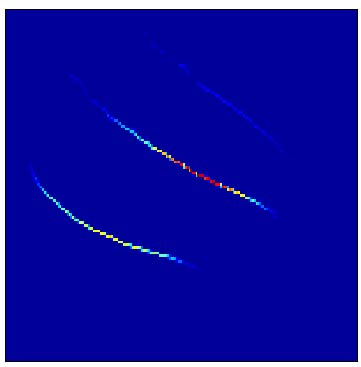
L'analyse temps-fréquence "classique" par distributions d'énergie quadratiques est confrontée à un compromis entre résolution conjointe et niveau des interférences. Dans l'exemple ci-dessus ("chirp" d'écholocation d'une chauve-souris, temps en abscisses, fréquence en ordonnées), un spectrogramme (à gauche) fournit une représentation approximative des trajectoires temps-fréquence des différentes composantes harmoniques, modulées en amplitude et en fréquence, qui composent le signal. Une meilleure précision peut être obtenue en ayant recours à la distribution de Wigner-Ville (au milieu), mais au prix de la création de contributions interférentielles entre composantes propres, qui en réduisent la lisibilité. Une façon de dépasser ce compromis est de recourir à la technique de "réallocation" (à droite), qui opère en déplaçant les valeurs du spectrogramme vers les centres de gravité locaux de la distribution de Wigner-Ville.
Après avoir développé pour cela des algorithmes de calcul efficaces susceptibles de s'appliquer à toute représentation bilinéaire, on a plus récemment montré (Thèse d'E. Chassande-Mottin, [R32]) comment la structure de champ des vecteurs de réallocation --- utilisé pour déplacer les valeurs dans le plan --- pouvait justifier l'introduction d'une variante différentielle de la méthode originale, permettant alors de l'utiliser aussi à des fins de traitement.
Plus spécifiquement, on a montré comment la réallocation d'une transformation en ondelettes préservait la possibilité d'estimation d'une singularité hölderienne isolée, tout en en améliorant la localisation [C112].
Une synthèse des principaux résultats obtenus dans ces directions est donnée dans [S17, S22]
(Collaboration avec F. Auger, du GE44-LRTI, Saint-Nazaire, et I. Daubechies de Princeton Univ., USA.).
détectionEn théorie de la détection, une étude particulière --- motivée par son application potentielle à la détection d'ondes gravitationnelles émises par des systèmes astrophysiques massifs ("binaires coalescentes") --- a été conduite dans le cas particulier de la détection de chirps en loi de puissance, la stratégie retenue reposant sur une idée d'intégration de chemin appliquée à un spectrogramme réalloué [R34, S14, S20]. On a montré comment la solution optimale (au sens du rapport de vraisemblance) pouvait se prêter à une mise en œuvre temps-fréquence au moyen de distributions adaptées, ouvrant en fait la voie à des approches robustes (dans le cas d’une connaissance imparfaite du signal et/ou du bruit) et à des stratégies de recherche itératives (pour diminuer le coût d’échantillonnage de l’espace des paramètres).
(Collaboration avec E. Chassande-Mottin, Albert Einstein Institut, Golm, Allemagne.)
haut de la page
localisationUne des vertus essentielles de la distribution de Wigner-Ville est de permettre une localisation parfaite dans le plan pour les "chirps" linéaires (signaux à phase quadratique). Une possibilité de généralisation à des chirps non linéaires passe par l’abandon du caractère quadratique de la distribution de Wigner-Ville et le recours à des fonctionnelles d’ordre supérieur. On s’est intéressé à ce problème de façon détaillée dans le cas quartique [R39, C100].
Dans le cas des signaux "chirps", la question de la localisation d'une distribution temps-fréquence sur une courbe du plan est discutée de façon très générale dans [R37, C108].
Un problème récurrent de l'analyse temps-fréquence étant d'estimer les caractéristiques d'un chirp, on s'y est intéressé par diverses approches complémentant les voies directes déjà étudiées (distributions localisées, réallocation...). On a ainsi considéré la question de décomposer un signal sur une "base" de chirps (ou plus précisément, de "chirplets"). La voie choisie --- qui, conceptuellement, généralise le but poursuivi par les techniques classiques de "matching pursuit", impraticables dans un tel contexte pour des raisons de complexité --- associe une approche par maximum de vraisemblance à une caractérisation locale à l'aide de certains des outils quartiques évoqués précédemment [R40, C101, C103].
(Collaboration avec J.C. O'Neill, de l'Univ. of Michigan, USA).
Plus récemment, une voie très différente a aussi été envisagée, qui consiste à caractériser un chirp en terme de trajectoire temps-fréquence, dont l'identification est obtenue par une technique de graphe (arbre de description minimal) appliquée à une carte temps-fréquence de maxima locaux d’une distribution d’énergie [R41, C107, C109].
(Collaboration avec O. Michel et A.O. Hero de l’Univ. of Michigan, USA.)
haut de la page
incertitudeDes résultats de type incertitude temps-fréquence, généralisant les inégalités classiques à la Heisenberg-Gabor-Weyl, ont été obtenus dans le cas de couples Mellin-Fourier, pour lequel on a défini des mesures d’encombrement adaptées [S16, C106, RI1]. Ceci a permis de mettre en évidence des fonctions maximalement localisées dans un contexte large bande, et d'en préciser leur comportement universel dans la limite à bande étroite.
Un corollaire a été d’établir une nouvelle forme de relation d’incertitude relative aux transformées en ondelettes continues [R38, C106].
Ces résultats ont également montré que des liens naturels existent entre minimum d’incertitude, positivité et séparabilité [R33].
haut de la page
complexitéOn s'est aussi intéressé à des questions relatives à la complexité d'un signal (définition et estimation) en utilisant des mesures issues de la théorie de l'information. On a ainsi exploré les possibilités offertes par l'information de Rényi appliquée à la distribution de Wigner-Ville et on a justifié la capacité qu'elle offre, dans certains cas, de dénombrer les composantes élémentaires (ou logons au sens de Gabor) constitutives d’un signal [R36].
(Collaboration avec O. Michel, R.G. Baraniuk, de Rice Univ, USA, et A.J.E.M. Janssen, des Philips Research Labs d’Eindhoven, Pays-Bas.)
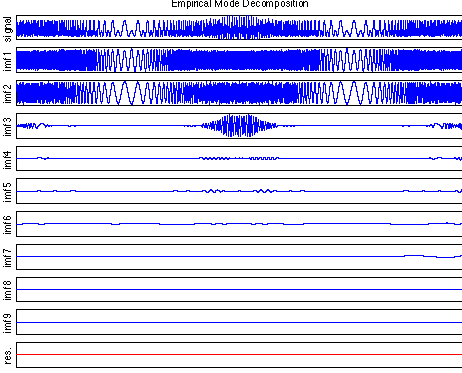
Empirical Mode DecompositionN.E. Huang et al. ont récemment introduit une technique nouvelle de décomposition adaptative d'un signal non stationnaire, appelée Empirical Mode Decomposition (EMD). Le principe en est d'identifier itérativement des composantes AM-FM de moyenne nulle et d'enveloppe symétrique en séparant localement (c'est-à-dire à l'échelle d'une oscillation) une contribution "rapide" d'une tendance plus "lente". L'EMD repose sur un principe intuitif très attractif (illustration du principe et codes Matlab ici) et fonctionne de façon remarquable dans des situations simples. Ainsi, dans l'exemple ci-dessous, un signal composite (1ère ligne) formé de la superposition de 2 signaux à modulation de fréquence sinusoïdale et d'un logon gaussien est décomposé essentiellement en ses 3 constituants élémentaires attendus (référencés IMF 1 à 3).
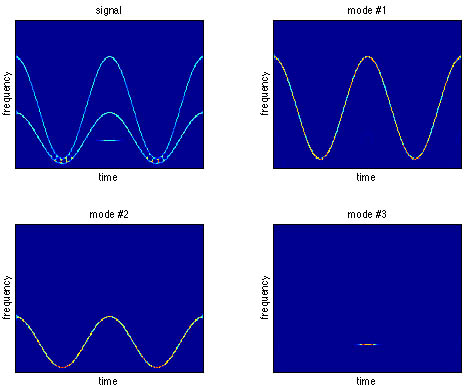
Le bien-fondé de cette décomposition peut être apprécié par l'analyse temps-fréquence (en l'occurrence un spectrogramme réalloué) du signal total et de chacun des modes identifiés. C'est ce qui est présenté ci-dessous, mettant en évidence que l'EMD réalise de facto un véritable filtrage variant dans le temps capable de séparer des composantes évolutives en recouvrement temporel et fréquentiel.
La version de base de l'EMD est conceptuellement simple, mais elle repose sur un certain nombre de dégrés de liberté (nature des interpolations, gestion des effets de bord, critères d'arrêt) laissés à l'appréciation de l'utilisateur. On s'est intéressé à cet aspect algorithmique et on a proposé [C126] un certain nombre de variations permettant un fonctionnement mieux contôlé de l'algorithme et certaines extensions : on a ainsi proposé une version locale du critère d'arrêt ainsi qu'une version en-ligne de l'algorithme, dans la perspective de la décomposition d'un flot de données.
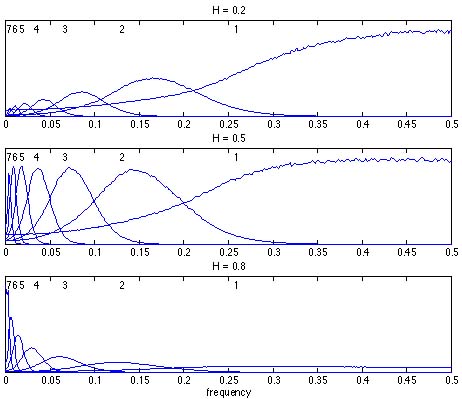
Par ailleurs, une difficulté fondamentale de l'EMD est de ne pas avoir de définition analytique et d'être essentiellement définie par un algorithme, ce qui ne permet pas une analyse simple de ses performances et limitations. On s'est attaché à mieux comprendre les résultats fournis par l'EMD dans trois situations typiques. La première est relative à l'identification d'une fréquence pure et au comportement de l'algorithme vis-à-vis des conditions d'échantillonnage. Cette étude a mis en évidence, pour une fréquence d'échantillonnage fixée, l'existence de zones critiques de fréquences susceptibles d'une bonne estimation, en lien avec les sous-harmoniques dyadiques de la fréquence d'échantillonnage [C126]. Cette observation a été complétée par une analyse quantitative de la séparabilité de deux fréquences pures [C126]. Enfin, on a considéré le problème de la décomposition d'un bruit large-bande et on a montré [R44] que, dans le cas du bruit gaussien fractionnaire, l'EMD s'organise spontanément en une structure équivalente de banc de filtres quasi-dyadiques, très proches de ce fournit une analyse en ondelettes dans le même contexte, fournissant une nouvelle approche à l'estimation de l'exposant de Hurst.
(Collaboration avec G. Rilling et P. Gonçalvès, INRIA Rhône-Alpes.)
haut de la page
longue dépendance et processus stablesLe processus Brownien fractionnaire, introduit par B. Mandelbrot et J.W. van Ness, est un paradigme classique pour l'auto-similarité statistique. Il possède la simplicité de ne dépendre que d'un paramètre, son exposant de Hurst, mais cette simplicité est aussi sa limitation en termes de modélisation, dans la mesure où des propriétés à petite échelle (régularité des trajectoires) se trouvent liées à des comportements à grande échelle (longue dépendance).
On a alors généralisé les premières analyses en ondelettes (portant sur le modèle du Brownien fractionnaire) et on a montré que celles-ci restaient adaptées à des classes plus larges de processus. Il en est ainsi des processus à longue dépendance et des processus linéaires fractionnaires stables (moyennant que l’on considère les log-coefficients d’ondelettes) [S12, C104, C105].
En fait, ce que l'on a montré, c’est que l'analyse en ondelettes offrait un langage naturel pour l'étude de classes très larges de processus auto-similaires et que la méthodologie proposée (dont une synthèse tutorielle est donnée dans [S11]) était très générale, pouvant non seulement s'appliquer de façon identique à différents types de données (continues ou ponctuelles, gaussiennes ou non...), sans présupposé sur la nature de l'auto-similarité mise en jeu, mais permettant également de caractériser cette dernière, en particulier par une mise en évidence statistiquement significative de la gamme d'échelles concernée.
(Collaboration avec P. Abry, L. Delbeke de KU Leuven, Belgique, D. Veitch du SERC-RMIT de Melbourne, Australie, et M.S. Taqqu de Boston Univ., USA.)
haut de la page
cascadesHormis le cas stable, l'essentiel des approches évoquées précédemment sont de second ordre, ce qui est évidemment une limitation dans les cas où des comportements non gaussiens peuvent être attendus. Une généralisation simple consiste à introduire des mesures à base de moments d'ordres supérieurs des coefficients d'ondelettes, ce qui permet d'accéder à des propriétés de multifractalité dans la limite des petites échelles.
On s'est récemment intéressé à ce type de questions, mais en se plaçant en fait dans un cadre plus général associé à une idée de cascades, telle qu'elle a été introduite il y a quelques années par B. Castaing en physique de la turbulence. Le point fort de ce type de modélisation est d'offrir un découplage entre les propriétés de moments et celles de lois d'échelle, permettant en particulier de valider l'existence éventuelle d'une invariance d'échelle dans des données expérimentales [C110].
(Collaboration avec P. Abry, P. Chainais et D. Veitch du SERC-RMIT de Melbourne, Australie.)
haut de la page
télétraficSe basant sur l'analyse multirésolution de processus ponctuels que l'on avait développée pour l’intermittence, on a appliqué le même type d’outils à un problème assez semblable dans la forme des données, quoique de nature très différente quant à son origine : le télétrafic informatique.
On a ainsi utilisé --- et montré la pertinence --- des approches basées sur les ondelettes pour mettre en évidence et caractériser des comportements statistiques non standards (auto-similarité, fractalité, longue dépendance) dans des données de trafic Ethernet, puis Internet [S11, C110].
(Collaboration avec P. Abry, P. Chainais et D. Veitch du SERC-RMIT de Melbourne, Australie. Etudes soutenues par le CNRS dans le cadre de son "Programme Télécommunications".)
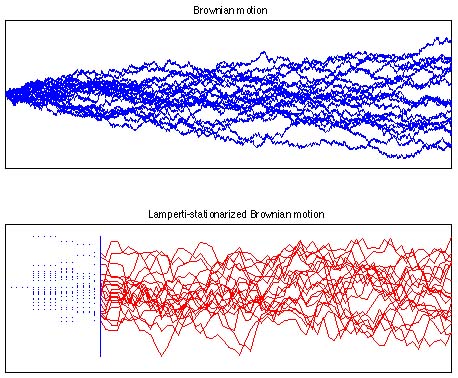
transformation de LampertiEn 1962, J.W. Lamperti a établi le résultat remarquable selon lequel les processus auto-similaires peuvent être mis en bijection avec les processus stationnaires au moyen d'une transformation simple que l'on appelle aujourd'hui transformation de Lamperti. Un exemple est donné ci-dessous.
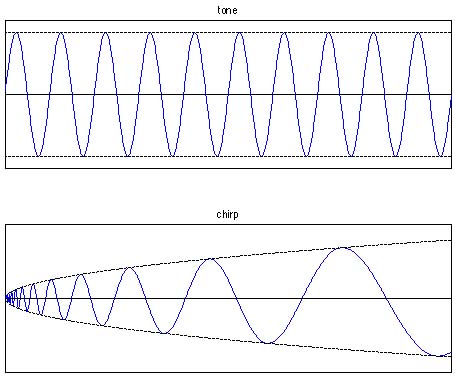
De façon surprenante, cette transformation a été l'objet de peu de travaux jusqu'à un passé récent, et l'on a étudié en détail ses propriétés et son intérêt (effectif ou potentiel) [S31] [RI3]. En fait, la transformation de Lamperti peut être envisagée d'au moins deux points de vue. D'une part, elle permet une manipulation indirecte des processus auto-similaires (filtrage, prédiction, etc.) en opérant sur leurs contreparties stationnaires. D'autre part, des outils stationnaires classiques peuvent être "lampertisés", offrant ainsi de nouvelles façons de manipuler les processus auto-similaires. En particulier, la transformée de Lamperti d'une fréquence pure n'est pas autre chose qu'un "chirp" de Mellin (figure ci-dessous), ce qui ouvre la voie à des représentations à base de Mellin pour les processus auto-similaires et, de façon plus intéressante, pour des variations que l'on peut imaginer sur ceux-ci [C124].
(Collaboration avec P. Borgnat et P.-O. Amblard, LIS Grenoble)
haut de la page
invariance d'échelle briséeDans la plupart des situations réelles, l'auto-similarité exacte (ou une invariance d'échelle complète) est une hypothèse bien trop forte et ce que l'on observe est généralement une forme affaiblie d'auto-similarité, ce que l'on désigne sous le terme générique d'invariance d'échelle brisée.
Comme premier exemple d'invariance d'échelle brisée, nous nous sommes intéressés à l'invariance d'échelle discrète (DSI, pour Discrete Scale Invariance), c'est-à-dire aux situations pour lesquelles l'égalité après changement d'échelle et renormalisation n'est obtenue que pour certains facteurs d'échelle privilégiés. Dans un tel cas, nous avons montré que les processus DSI "délampertisés" s'identifient à des processus cyclostationnaires, ce qui permet de les analyser avec des outils classiques dans le domaine transformé [R43][C117][C118]. Réciproquement, la transformation de Lamperti a été utilisée avec succès pour synthétiser des processus DSI à partir de processus cyclostationnaires [C121].
Un deuxième exemple d'invariance d'échelle brisée correspond aux situations pour lesquelles il existe des limites intrinsèques (en temps et/ou pour les valeurs des processus eux-mêmes) entre lesquelles l'invariance d'échelle est confinée, ce que l'on appelle invariance d'échelle de taille finie. En se basant sur les groupes de transformation convenables qui prennent explicitement en compte les limites associées aux effets de taille finie, nous avons proposé une transformation de Lamperti généralisée destinée à mettre en correspondance les processus à invariance d'échelle de taille finie et les processus stationnaires [C124][C125].
(Collaboration avec P. Borgnat et P.-O. Amblard, LIS Grenoble)