16 mars - 17 mars 2009
ENS-Lyon --- LIP


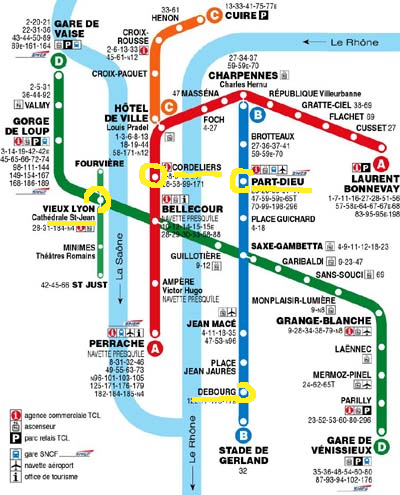

Lieu
Amphi J le lundi 16/03/2009Amphi L le mardi 17/03/2009.
Les amphi J et L sont situés au rez-de-chaussée dans la partie nord du batiment (dite aussi partie des locaux enseignements) , à la place du "y" du plan ci-dessus.
Programme prévisionel
Acceuil 9h30
Lundi 16 mars amphi J, 10h
- 10h: Christine Tasson
- Comment inverser le développement de Taylor dans les réseaux de la logique linéaire ?
Résumé :
En logique linéaire, la règle la plus compliquée est certainement la promotion. D'un point de vue graphique, cette règle délimite un sous-réseau qui peut alors être effacé ou dupliqué un nombre de fois arbitrairement grand. Intuitivement, le programme correspondant à ce sous-réseau est une fonction que l'on va pouvoir appeler à loisir.
A la suite d'une étude sémantique, Ehrhard et Regnier ont introduit la logique linéaire différentielle ainsi que les réseaux différentiels associés, dans lesquels, la promotion est remplacée par trois constructions élémentaires. Les effacements et duplications deviennent explicites. Via le développement de Taylor, on peut alors encoder les réseaux avec promotions par une somme infinie de réseaux différentiels.
On peut alors se demander comment inverser cette opération : Étant donnés plusieurs réseaux différentiels, proviennent-ils d'un même réseau de la logique linéaire ? Si oui, quel est ce réseau ?
Travail en commun avec Michele Pagani.
- 10h45: Simon Perdrix (PPS Université Paris Diderot & LFCS, University of Edinburgh)
- Quantum Graph States and the necessity of Euler Decomposition
Résumé:
Coecke and Duncan recently introduced a categorical formalisation of
the interaction of complementary quantum observables. We use
their diagrammatic language to study graph states, a computationally
interesting class of quantum states. We give a graphical proof
ofthe fixpoint property of graph states. We then introduce a new
equation, for the Euler decomposition of the Hadamard gate, and
demonstrate that Van den Nest's theorem --locally equivalent graphs
represent the same entanglement-- is equivalent to this new
axiom. Finally, we prove that the Euler decomposition equation is
not derivable from the existing axioms.
Joint work with Ross Duncan, Oxford University.
Pause 11h30
Lundi 16 mars amphi J, 11h45
- 11h45: Luigi Santocanale (LIF, Université Aix-marseille)
- Sur la géométrie de la "softness" : le problème du mot pour les catégories avec produits et coproduits
Résumé: La propriété de la "softness" caractérise les catégories avec produits et coproduits libres. Cette propriété décrit hom(X x Y,A + B) -- l'ensemble des flèches de X x Y vers A + B -- comme un certain "pushout", c-a-d. comme un certain quotient des ensembles hom(X,A+B), hom(Y,A+B), hom(X x Y,A), hom(X x Y,B). Une analyse fine de ce quotient permet d'établir plusieurs propriétés des catégories avec produits et coproduits libres, et de deviser un algorithme de décision pour le problème du mot (en présence d'unités) qui est polynomiale.
Travail en collaboration avec Robin Cockett, de l'Université de Calgary
Lundi 16 mars amphi J, 13h 45
- 13h45: Romain Demangeon
- Terminaison en pi-calcul
Résumé:
La question de la terminaison des systèmes concurrents, et particulièrement des systèmes dont la topologie change dynamiquement, est intuitivement trop complexe pour pouvoir être résolue par une "mise
en parallèle" de techniques connues de terminaison séquentielle. On présentera dans cet exposé, après avoir rappelé le formalisme du pi-calcul, des systèmes de types pour la terminaison basés sur la notion de poids. On discutera de l’expressivité de ces systèmes et de la
complexité de l’inférence.
- 14h30: Ralph Matthes (IRIT)
- Monadic translation of intuitionistic and classical sequent calculus
(joint work with José Espírito Santo and Luís Pinto)
Résumé:
Monadic translations of intuitionistic and classical sequent calculi
into intuitionistic and classical lambda calculi are studied that
strictly simulate reduction steps in the sense that each rewrite step
in the source is mapped to at least one rewrite step in the target,
thus allowing to infer strong normalization for the source from that
of the target in a purely syntactic manner.
The TYPES'08 post-proceedings will contain the intuitionistic part,
namely the translation of system lambdaJmse, which is a notational
variant of the intuitionistic fragment of the call-by-name subsystem
of lambda-bar-mu-mu-tilde of Curien and Herbelin, into a variant of
Moggi's monadic meta-language, where the rewrite relation includes
extra permutation rules that may be seen as variations of the
"associativity" of the monadic bind operation. By instantiation
with the identity monad, this yields a simulation into simply-typed
lambda calculus with an extra permutation rule.
The new contribution of this talk is the treatment of the full
(classical) call-by-name fragment of lambda-bar-mu-mu-tilde. The
target of the translation is a monadic extension of Parigot's
lambda-mu calculus. Only the added monad comes with classical
features, hence, unlike Parigot's calculus, the classical logic
machinery is confined to monadic types. It is this new monadic
meta-language for classical logic, named monadic lambda-mu, through
which factors a strictly reduction-preserving embedding into
simply-typed lambda calculus with some extra reduction rules. The
monadic translation is even easier than in the intuitionistic case,
due to a new hybrid mu-rule (combining classical and monadic aspects),
and the final embedding into the extended simply-typed lambda calculus
is done by a CPS translation.
Résumé:
Monadic translations of intuitionistic and classical sequent calculi
into intuitionistic and classical lambda calculi are studied that
strictly simulate reduction steps in the sense that each rewrite step
in the source is mapped to at least one rewrite step in the target,
thus allowing to infer strong normalization for the source from that
of the target in a purely syntactic manner.
The TYPES'08 post-proceedings will contain the intuitionistic part,
namely the translation of system lambdaJmse, which is a notational
variant of the intuitionistic fragment of the call-by-name subsystem
of lambda-bar-mu-mu-tilde of Curien and Herbelin, into a variant of
Moggi's monadic meta-language, where the rewrite relation includes
extra permutation rules that may be seen as variations of the
"associativity" of the monadic bind operation. By instantiation
with the identity monad, this yields a simulation into simply-typed
lambda calculus with an extra permutation rule.
The new contribution of this talk is the treatment of the full
(classical) call-by-name fragment of lambda-bar-mu-mu-tilde. The
target of the translation is a monadic extension of Parigot's
lambda-mu calculus. Only the added monad comes with classical
features, hence, unlike Parigot's calculus, the classical logic
machinery is confined to monadic types. It is this new monadic
meta-language for classical logic, named monadic lambda-mu, through
which factors a strictly reduction-preserving embedding into
simply-typed lambda calculus with some extra reduction rules. The
monadic translation is even easier than in the intuitionistic case,
due to a new hybrid mu-rule (combining classical and monadic aspects),
and the final embedding into the extended simply-typed lambda calculus
is done by a CPS translation.
- 15h15: Germain Faure
- Stratégies de réécriture et lambda-calculs avec motifs
Résumé: Dans cet exposé, je montrerai que les lambda-calculs avec motifs sont particulièrement bien
adaptés pour donner une sémantique aux langages de stratégies de réécriture.
adaptés pour donner une sémantique aux langages de stratégies de réécriture.
Pause 16h
Lundi 16 mars, 16h30 amphi J
- 16h30: Yves Lafont / Pierre Rannou
- Réécriture de diagrammes
- 17h15: Sergei Soloviev (IRIT)
- Les variétés de catégories symétriques monoidales fermées et la
dépendance de diagrammes.
Résumé: Il est démontré qu’il existe un nombre infini de diagrammes dans
les catégories symétriques monoidales fermées tels que la commutativité
d’un diagramme n’implique pas la commutativité de l’autre. Comme
conséquence, il existe un nombre infini de sous-variétés de la classe de
catégories symétriques monoidales fermées (dans le sens de l’algèbre
universelle). Les diagrammes en question sont représentés par les paires
de dérivations dans la logique linéaire intuitionniste ayant le même
graphe. Une interprétation possible de notre résultat est l’existence d'une
infinité de relations d’équivalence catégoriques sur l’ensemble des
dérivations. Des applications des méthodes de la théorie de démonstration
à l'algèbre seront évoquées.
Mardi 17 mars, 9h00 amphi L
- 9h: Cody Roux
- La terminaison par analyse de taille: une instance de l'annotation semantique.
Résumé: Dans le système T de Gödel, il y a une décroissance structurelle
dans la partie droite de la règle du récurseur par rapport à la partie
gauche. Celle-ci permet de construire une sémantique dans les ensembles,
par induction sur la taille de (l'interprétation) de cet argument. Cela
nous donne-t-il la normalisation forte pour autant? Traditionnellement
non, il faut construire une interprétation plus complexe, dans le monde
des candidats de réductibilité. Cependant, en utilisant la technique de
l'annotation sémantique, inventée au premier ordre par Zantema et
développée a l'ordre supérieur par Hamana, il est possible de déduire la
normalisation du système T à partir de cette interprétation
fonctionnelle. Nous montrons en outre que ce genre d'interprétation
permet de justifier la correction d'une classe de méthodes de
terminaison dites "à base de taille".
- 9h45: Karim Nour (LAMA)
- Quelques résultats de forte normalisation par traduction
Résumé: Je présente une démonstration de la forte normalisation de la déduction naturelle classique propositionnelle (avec l'implication, la conjonction, la disjonction et les réductions commutatives) en utilisant une traduction dans le lambda-mu-calcul simplement typé. J'étends ensuite le résultat de Mendler pour des équations récursives pour ce système.
Pause 10h30
Mardi 17 mars, 11h, amphi L
- 11h: Denis Cousineau (LIX - INRIA Saclay Île de France)
- Un théorème de complétude pour la déduction minimale modulo
Résumé:
La déduction modulo est une extension de la logique des prédicats du premier
ordre dans laquelle les axiomes sont remplacés par des règles de réécriture.
Ce cadre logique permet d'exprimer de nombreuses théories comme l'arithmétique,
la théorie des types simples, certaines variantes de la théorie des ensembles, ou encore
les systèmes de types purs. Un point-clé de ce cadre logique est de trouver une caractérisation
des théories possédant la propriété de normalisation forte. Dowek et Werner ont exhibé une
condition sémantique suffisante pour assurer la normalisation forte d'une théorie : ils ont démontré
un théorème de correction de la forme : si la théorie possède un modèle (d'une certaine forme) alors
elle est fortement normalisante. Dans cet exposé, je montrerai comment affiner leur notion de modèle
afin d'obtenir non plus seulement la correction mais aussi la complétude de ce type de modèles :
une théorie est fortement normalisante si et seulement si elle possède un modèle de ce genre.
Ce résultat contribue à l'idée que la propriété de forte normalisation n'est pas seulement une
notion de théorie des preuves, mais aussi une notion de théorie des modèles.
Mardi 17 mars, 13h30, amphi B (3ème étage, invité par le DI de l'ENS)
- Jean-Yves Marion, (LORIA)
Virologie théorique et le problème de la détection
Résumé :
Dans cet exposé, nous traiterons de virologie informatique et de codes
malveillants. Si les enjeux de société sont clairs, la recherche
académique ne s'est guère intéressée à ce sujet. Pourtant, nous
verrons que la virologie s'appuie sur des résultats importants comme
le théorème de récursion de Kleene ou comme les systèmes
autoreproducteurs (von Neumann). Nous dresserons un rapide état
général de la recherche et des problèmes soulevés. En particulier,
nous aborderons la délicate question de la détection des malwares.
Pause 14h30
Mardi 17 mars, 15h, amphi L
- 15h: Claudia Faggian
- Partial Orders, Event Structures, and Linear Strategies
Résumé:
We introduce a game-semantical model where strategies are partial
orders, and composition is merging of orders.
Our setting generalizes the "merging of orders" introduced by Girard
in the setting of Ludics, and develops ideas propounded by Hyland.
On this basis, to bridge between Game Semantics and Concurrency, we
explore the relation between Event Structures and Linear Strategies.
The former are a true concurrency model introduced by Nielsen,
Plotkin, Winskel, the latter a family of linear innocent strategies
developed starting from Girard's work.
- 15h45: Dominique Duval
- Un cadre formel pour parler de "logique"
Résumé:
Cet exposé relève de la thématique générale du groupe GEOCAL :
trouver au sein de la logique et des mathématiques des outils
permettant la modélisation abstraite des programmes.
Je présenterai un cadre formel pour parler de "logique",
avec lequel nous développons des outils pour modéliser
certaines propriétés liées aux effets
dans les langages de programmation.
Ce cadre mathématique repose sur des notions catégoriques
connues depuis les années 1960, en particulier les fractions
de Gabriel et Zisman et les esquisses projectives d'Ehresmann.
Plan du site de l'ENS de Lyon
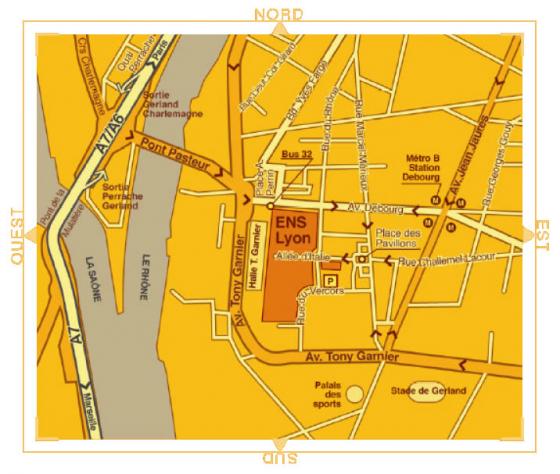
Se rendre à l'ENS de Lyon
Voir cette page. Un fléchage vers l'amphi sera assuré. Si vous êtes perdu, rendez-vous au LIP "coin café", 3ème étage du bâtiment central.Hôtels proches de l'ENS
Une formule intéressante 35 euros et plus près* Bed in City
A partir de 45 Euros
* Etap Hotel de Gerland
A partir de 68 Euros
* Hôtel IBIS de Gerland
Autres hôtels
