| Vincent Langlois | ||
| professional website |
Theoretical models
The formation of sand ripples can be understood by a linear stability analysis of the surface of the sand bed. The main approximation is to consider that the fluid moves much quicker than the ripples themselves, which is usually reasonable. But contrary to the oscillatory case, where the wavelength scales with the amplitude of the waves, for a continuous flow there is no obvious lengthscale in the system. The mechanism can be described simply in 2D: let us consider that the quantity of grains transported by the water increases with the shear stress exerted by the fluid on the sand surface. Where the shear stress increases, the flux of rolling grains increases as well: sand is eroded from the bed. For the same reason, sand is deposited where the flux of grains decreases. Therefore the growth of a bump can be determined easily:
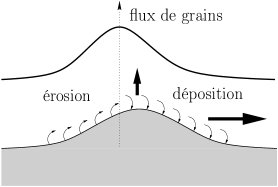
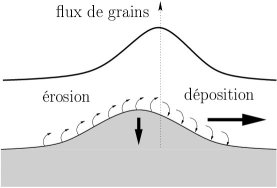
The stability analysis thus consists in finding how the phase shift between the shear stress and a bed perturbation varies with its wavelength. We have done that in 3D by solving analytically the linearized Navier-Stokes equation around a linear shear profile over a bumpy surface of wavenumbers (kx,ky). The flux of grains is then calculated by applying a transport law, and the evolution of the surface follows from conservation of mass. Thus we can calculate the following stability diagram:
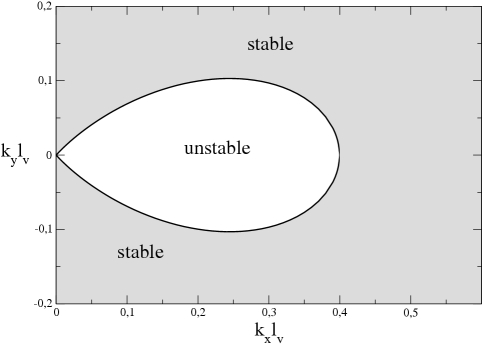
|
© Copyright 2007-23.
Vincent Langlois
|  | 
|


