| Vincent Langlois | ||
| professional website |
Theoretical models
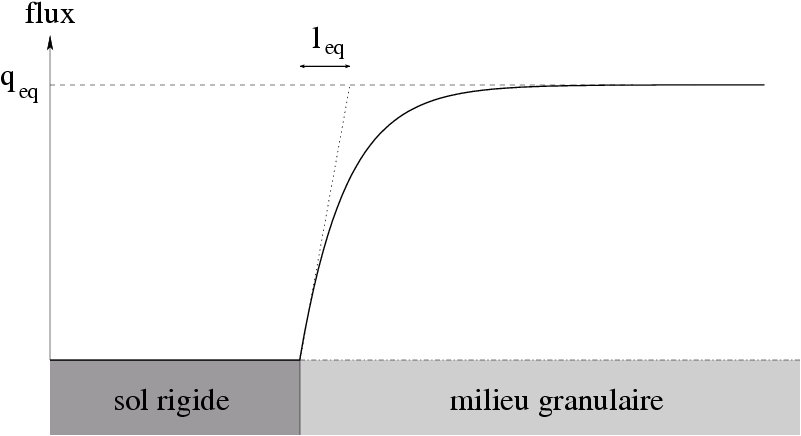
The flow always makes the sand bed unstable: the fluid is always "in advance" compared to the topography. Therefore, whatever its wavelength, a perturbation will grow. Even worse, the smaller it is, the faster it grows. The usual way to solve this problem is to introduce gravity in the problem, by considering that the threshold of motion depends on the local slope: it's easier to dislodge a grain on a downward slope. Unfortunately, the complete calculation in this case predicts a wavelength that's about ten times smaller than the ripples we observe experimentally.
In order to solve that problem, we have applied a BCRE-type model to the static bed and the layer of rolling grains, in order to take into account their inertia: for instance, if the velocity of the flow suddenly increases, the flux of grains cannot adapt immediately. There must be a transient regime during which new grains need to be dislodged and accelerated, which takes a certain time, and a certain length. This is similar to what has been introduced as a saturation length in the context of aeolian sand transport.
|
© Copyright 2007-23.
Vincent Langlois
|  | 
|


