Deformation estimations on a synthetic signal

Copyright (C) 2017 Adrien MEYNARD

This program is free software; you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation; either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/.

Author: Adrien MEYNARD Email: adrien.meynard@univ-amu.fr Created: 2017-12-19

Contents

Load signal

clear all; close all; clc;

warning off;
addpath('cwt');
addpath('deform_estimation');

load('signals/toy_sig_paper');
T = length(y);

Joint estimation

Dt = 200; % temporal subsampling for the deformation estimation
dgamma0 = ones(1,T); % gamma'(t) initialization
a0 = ones(1,T); % a(t) initialization

wav_typ = 0; % wavelet type (cf. cwt.m)
wav_paramWP = 25; % corresponding parameter for warping estimation
wav_param = 500; % corresponding parameter for spectrum and AM estimations

NbScales = 106;
scalesAM = 2.^(linspace(-1,3.5,NbScales));
subrate = 7; % subsampling step for the scales to ensure the covariance invertibility
scalesWP = scalesAM(1:subrate:end);

stopWP = 2e-2; % minimal gap between two steps in the gradient
itWP = 6; % number of gradient iterations

r = 1e-3; % regularization parameter

Nf = 2500; % number of frequencies for spectrum estimation
NbScalesS = 212;
scalesS = 2.^(linspace(-1,3.5,NbScalesS)); % for spectrum estimation

Nit = 10; % maximal number of iterations in the joint estimation
stop_crit = 1e-3; % relative update threshold

paramWAV = {wav_typ,wav_param,wav_paramWP};
paramAM = {'AM',scalesAM,r}; % AM (model without noise)
paramWP = {scalesWP,itWP,stopWP};
paramS = {scalesS,Nf};

tic;
[aML, dgammaML, Sxest, evol_crit] = estim_altern(y,Dt,dgamma0,a0,paramWAV,paramWP,paramAM,paramS,stop_crit,Nit);
toc;

 Iteration 1 
 Relative update WP: Inf % 
 Relative update AM: 71.71 %

 Iteration 2 
 Relative update WP: 34.37 % 
 Relative update AM: 33.32 %

 Iteration 3 
 Relative update WP: 35.52 % 
 Relative update AM: 105.53 %

 Iteration 4 
 Relative update WP: 71.20 % 
 Relative update AM: 72.27 %

 Iteration 5 
 Relative update WP: 1.75 % 
 Relative update AM: 11.91 %

 Iteration 6 
 Relative update WP: 0.11 % 
 Relative update AM: 0.28 %

 Iteration 7 
 Relative update WP: 0.01 % 
 Relative update AM: 0.07 %

Elapsed time is 69.789505 seconds.

Deformations estimation

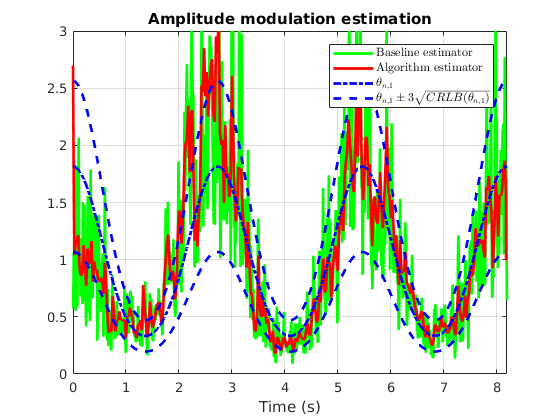
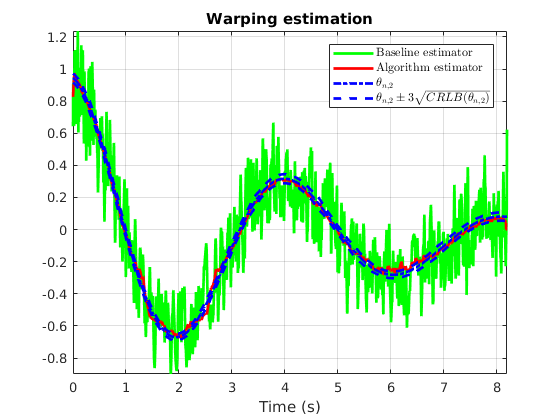
addpath('analysis')

Wy = cwt(y,scalesAM,0,wav_param);

thetaWP_B = baselinewarpest(Wy,scalesAM);
thetaAM_B = baselineAMest(Wy);

thetaWPV = log2(dgamma(1:Dt:end)).';
thetaAMV = (a(1:Dt:end).^2).';
bWP = crlbWP(thetaWPV,thetaAMV,Sx+eps,scalesWP,wav_typ,wav_paramWP);
WPinf = thetaWPV - 3*sqrt(bWP);
WPsup = thetaWPV + 3*sqrt(bWP);

bAM = crlbAM(thetaAMV,scalesAM);
AMinf = thetaAMV - 3*sqrt(bAM);
AMsup = thetaAMV + 3*sqrt(bAM);

t = linspace(0,(T-1)/Fs,T);
th = t(1:Dt:end);
figure;
plot(t,thetaAM_B,'g',t,aML.^2,'r',t,a.^2,'b-.',th,AMinf,'b--',th,AMsup,'b--','linewidth',2); grid on;
title('Amplitude modulation estimation');
legend({'Baseline estimator','Algorithm estimator','$\theta_{n,1}$','$\theta_{n,1} \pm 3\sqrt{CRLB(\theta_{n,1})}$'},'Interpreter','latex'); axis([0 t(end) 0 3]);
xlabel('Time (s)'); ylabel('');

figure;
plot(t,thetaWP_B,'g',t,log2(dgammaML),'r',t,log2(dgamma),'b-.',th,WPinf,'b--',th,WPsup,'b--','linewidth',2); grid on; axis tight;
title('Warping estimation');
legend({'Baseline estimator','Algorithm estimator','$\theta_{n,2}$','$\theta_{n,2}\pm 3\sqrt{CRLB(\theta_{n,2})}$'},'interpreter','latex');
xlabel('Time (s)'); ylabel('');

Spectrum estimation

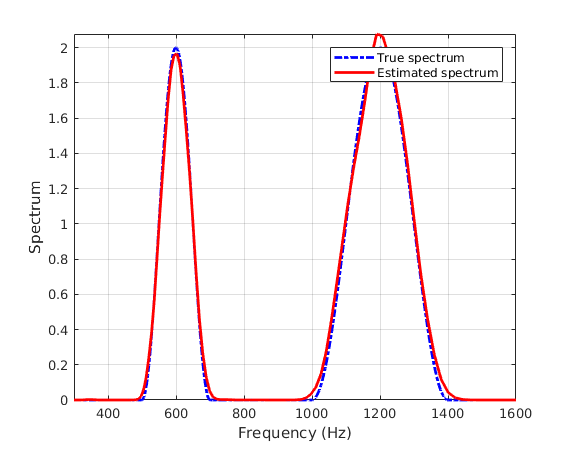
freq = linspace(0,Fs,2*Nf - 1);

figure;
plot(freq,Sx,'-.b',freq,Sxest,'r','linewidth',2);
xlabel('Frequency (Hz)');ylabel('Spectrum');
grid on; axis tight;
legend('True spectrum','Estimated spectrum');
V=axis; axis([300 1600 0 V(4)]);

Stopping criterion

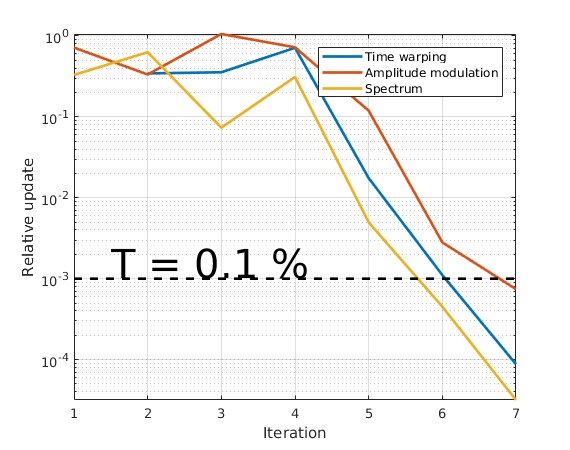
Nit = size(evol_crit,1);
figure;
semilogy(evol_crit,'linewidth',2);
hold on; semilogy(1:Nit,0.001*ones(Nit,1),'k--','linewidth',2); % threshold
text(1.5,1.5e-3,'\fontsize{30}T = 0.1 %');
legend('Time warping','Amplitude modulation','Spectrum'); axis tight;
grid on; xlabel('Iteration'); ylabel('Relative update');

MSE

errAM = (aML(:).^2 - a.^2).^2;
errAM = errAM(Dt:end); % First sample of thetaAM is rejected because of boundaries effect
mseAM = mean(errAM.^2);
mseAM0 = mean((thetaAM_B(:) - a.^2).^2);
mseWP = mean((log2(dgammaML(:)) - log2(dgamma)).^2);
mseWP0 = mean((thetaWP_B(:) - log2(dgamma)).^2);
fprintf('\nMean square errors: \n\n AM estimation:\n Baseline method: %.2e \n Algorithm estimation: %.2e \n\n Time Warping estimation:\n Baseline estimation: %.2e \n Algorithmestimation: %.2e\n',[mseAM0,mseAM,mseWP0,mseWP])

Mean square errors: 

 AM estimation:
 Baseline method: 2.01e-01 
 Algorithm estimation: 7.01e-02 

 Time Warping estimation:
 Baseline estimation: 2.32e-02 
 Algorithmestimation: 4.91e-04

Published with MATLAB® R2017a