We prove "untyping" theorems: in some typed theories (semirings, Kleene algebras, residuated lattices, involutive residuated lattices), typed equations can be derived from the underlying untyped equations. As a consequence, the corresponding untyped decision procedures can be extended for free to the typed settings. Some of these theorems are obtained via a detour through fragments of cyclic linear logic, and give rise to a substantial optimisation of standard proof search algorithms.
Using a proof assistant revealed really useful to obtain these proofs: they are quite combinatorial and often lead to tedious and boring case analyses, for which a pencil and paper proof would hardly be trusted -- even by the author. Once the key lemmas are stated in the correct way, and except for some conceptually involved steps, most of the proofs can be obtained by running the right induction, followed by simple tactics to perform hypotheses inversion (case analysis), and automatic resolution of well-defined classes of goals (e.g., typing judgements are derived by unification, using eauto; equality of lists modulo cyclic permutation is handled using a dedicated tactic).
Coq proofs are split into three self-contained files:
The previous links point to the coqdoc generated pages; here are the original files, with proofs: utas.v mll.v mall.v ring.v (these files compile at least with Coq v8.3 - revision 13769).
In the previous files, the presentation is syntactical, and really close to the aforementioned paper. For monoids, semirings, and Kleene algebras, these ideas were also implemented in the ATBR Coq library, so that the tactics we developed for these structures work on heterogeneous binary relations or rectangular matrices. The main difference in the corresponding ATBR proofs comes from the fact that we use dependent types (rather than typing judgements about an untyped syntax) to directly capture models like binary relations or matrices.
(The raw data corresponding to the figures below can be found in the above archive.)
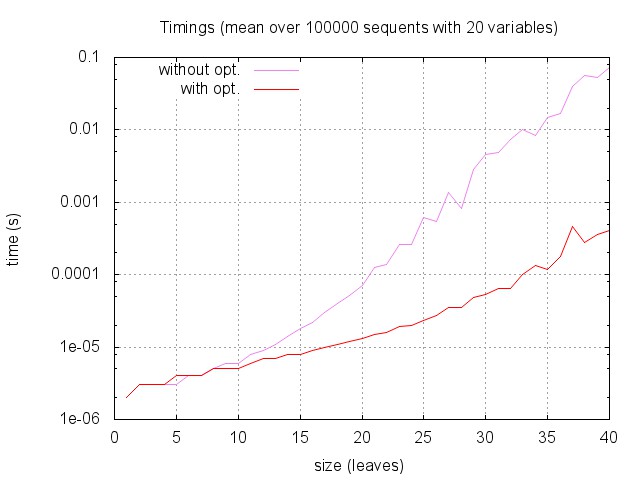
Here are the global timings as a function of sequent size: for each sequent size (from 1 to 40) we measured the time required to answer by the two versions of the algorithm on 100 000 random sequents with 20 variables. (Note that the time scale is logarithmic.)

Then, global timings as a function of number of variables: for each number of variables (from 0 to 40) we measured the time required to answer by the two versions of the algorithm on 100 000 random sequents with 30 leaves.
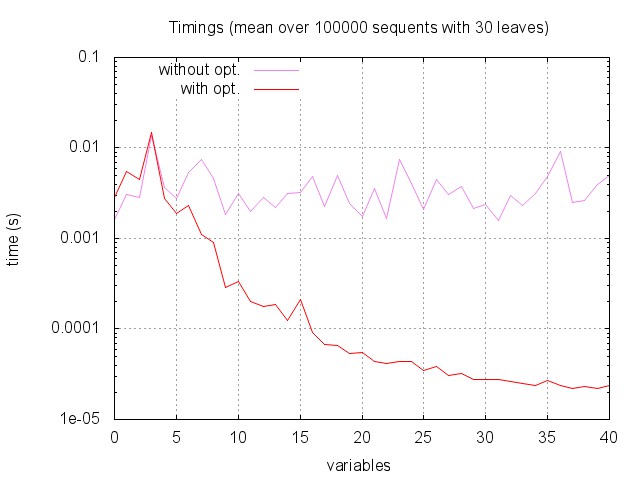
While the optimisation does not help much if there are only one or two variables, the improvement is striking when we have more than five variables. In fact, the more variables we have, the harder it gets to find square (and hence, potentially provable) sequents. This explains why, when using our optimisation, the overall complexity decreases with the number of variables.
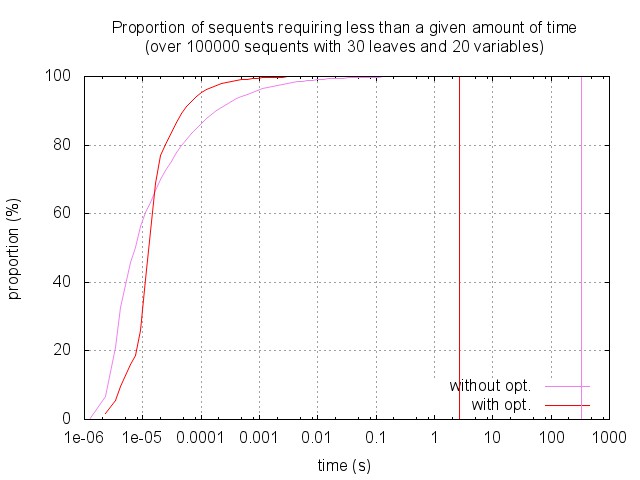
The empirical complexity is highly stochastic, so that the previous mean times are not so good to describe the actual behaviour of the algorithm. The figure below shows the proportion of sequents that can be solved in a given amount of time, among sequents with a fixed size and number of variables. While 70% of the sequents are solved in less that 1e-5s (with or without optimisation), some of them require much more time: up to three minutes without optimisation, and up to one second with the optimisation.
Accordingly, here is the distribution of timings and number of calls to the synchronous phase. (Note that the two scales are logarithmic.) As expected these values are highly correlated, this allows us to focus on synchronous calls in the sequel.
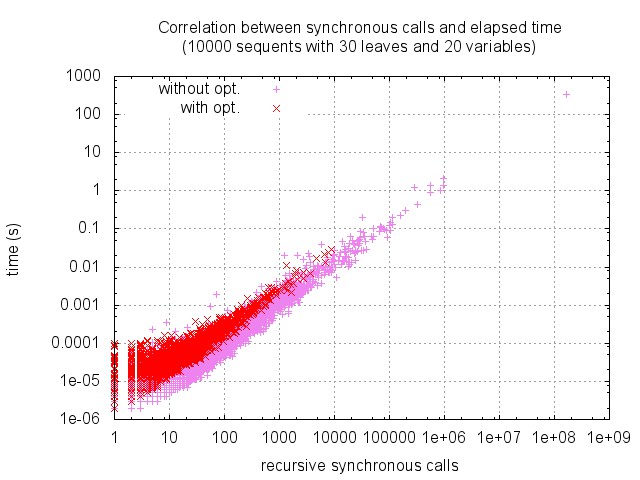
Very few sequents are provable, and many sequents are square: as shown below, about 90% of sequents with 30 leaves and 20 variables are square (and less than 0.1% are provable). This seems to entail that the optimisation cannot be so efficient.
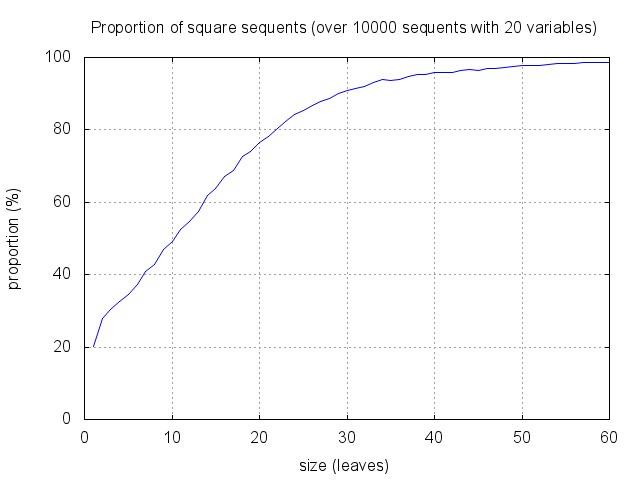
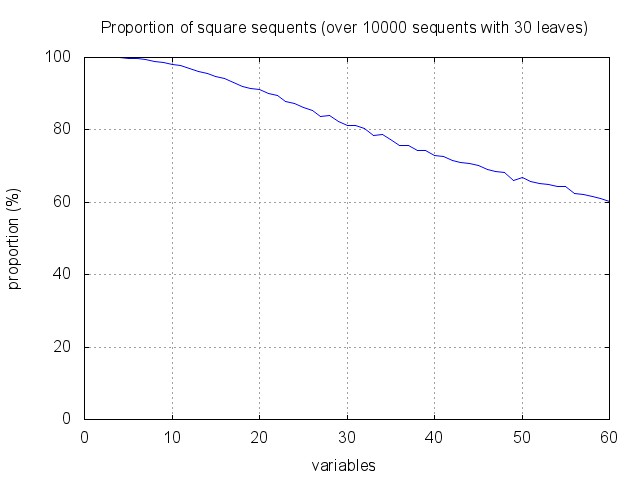
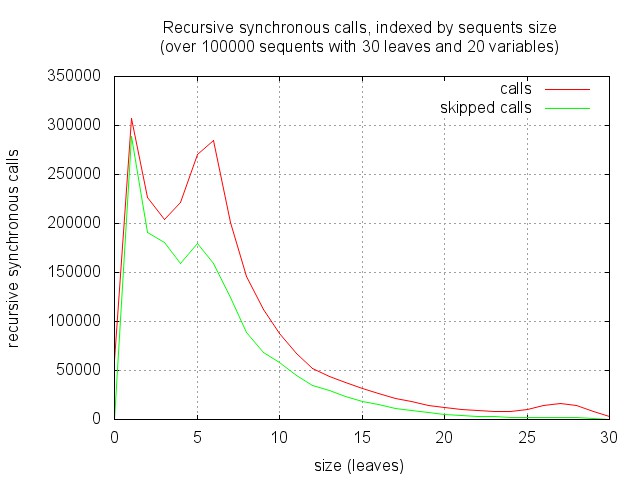
One can however notice that the proportion of square sequents increase with the size, and decreases with the number of variables. And in fact, proof search tend to focus quite rapidly on small sequents, where the heuristic gets more efficient. This is illustrated by the figure below. It corresponds to running proof search and recording the distribution of recursive synchronous calls with respect to the size of the corresponding sequents. As expected, there are few calls to "big" sequents (of the starting size 30), the algorithm mainly works on sub-sequents of less than half this size.