A Recursive Binary Gcd Algorithm
Damien Stehlé and Paul Zimmermann
Abstract:
The binary algorithm is a variant of the Euclidean algorithm that performs
well in practice. We present a quasi-linear time recursive algorithm that
computes the greatest common divisor of two integers by simulating a
slightly modified version of the binary algorithm. The structure of our
algorithm is very close to the one of the well-known
Knuth-Schönhage fast gcd algorithm;
although it does not improve on its $O(M(n) \log n)$ complexity,
the description and the proof of
correctness are significantly simpler in our case. This leads to a
simplification of the implementation and to better running times.
Download: pdf © Springer-Verlag.
Slides in French: ps.gz,
pdf.
Errata
We thank Dan Bernstein and Bo-Yin Yang for pointing out that Gn = 0,1,-1,5,-9,29,-65,181,-441,1165,..., which
is the worst-case for Theorem 2, is not necessarily the worst-case for the algorithm (as claimed in Section 6.2).
More details here. Also, in Theorem 3, the inputs
that are claimed to reach the upper bound do not achieve that property as they are not even integers.
We thank Niels Möller for having pointed out to us a mistake in Figure 6
of the article. It should be:
Figure 1:
Algorithm Half-GB-gcd.
![\begin{figure}\algorithme{
{\bf Algorithm} Half-GB-gcd.\\
{\bf Input:} $a,b$\ s...
...turn $j_1+j_0+j_2, \ R_2 \cdot [q]_{j_0} \cdot R_1, \ c , \ d$.
}\end{figure}](img2.png) |
Each time algorithm Half-GB-gcd is called by algorithm
Fast-GB-gcd, the parameter k is chosen as
.
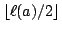Some Statistical Tests Related to the GB Division
Distribution of the quotient of GB(a,b) when a and b are chosen uniformly
in [|1,2^10-1|] with nu_2(b) > nu_2(a). 10^6 samples. In percentages.
Notice that quotients with the same bit length appear with equal frequencies.
| |q| |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
17 |
19 |
21 |
23 |
25 |
27 |
29 |
31 |
>32, <64 |
>64 |
| mean |
66.68 |
16.74 |
4.17 |
4.13 |
1.02 |
1.04 |
1.05 |
1.03 |
0.26 |
0.25 |
0.26 |
0.26 |
0.27 |
0.25 |
0.26 |
0.26 |
1.04 |
1.04 |
Average number of divisions in the GB Euclidean execution starting from a,b
when a and b are chosen uniformly in [|1,2^n-1|] with nu_2(b) > nu_2(a).
10^3 samples if n<=100, 10 samples if n>=200.
| n |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
| mean |
4.9 |
10.0 |
15.1 |
20.3 |
25.6 |
30.6 |
35.6 |
40.8 |
45.8 |
51.0 |
104 |
155 |
207 |
253 |
308 |
357 |
406 |
469 |
518 |
| worst |
10 |
18 |
26 |
31 |
35 |
44 |
50 |
60 |
65 |
67 |
117 |
162 |
226 |
271 |
324 |
385 |
445 |
480 |
546 |
Distribution of the quotients appearing in the GB Euclidean execution starting from a,b
when a and b are chosen uniformly in [|1,2^n-1|] with nu_2(b) > nu_2(a). 1 sample. In percentages.
| n |
nbr of quotients |
|q|=1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
>16 |
| 1000 |
491 |
64.6 |
18.9 |
3.9 |
4.1 |
1.0 |
0.6 |
1.2 |
0.4 |
<=5.0 |
| 2000 |
1029 |
67.5 |
15.9 |
3.3 |
3.7 |
1.3 |
1.6 |
0.8 |
1.7 |
<=4.2 |
| 3000 |
1588 |
66.8 |
17.3 |
4.0 |
3.7 |
1.6 |
1.4 |
0.8 |
0.8 |
<=3.6 |
| 4000 |
2085 |
68.1 |
16.1 |
4.3 |
3.9 |
1.0 |
0.9 |
1.1 |
0.9 |
<=3.7 |
| 5000 |
2593 |
66.6 |
17.1 |
4.0 |
4.0 |
1.1 |
1.0 |
1.1 |
1.1 |
<=4.0 |
| 6000 |
3058 |
67.0 |
15.7 |
4.3 |
4.4 |
1.4 |
0.8 |
1.1 |
0.9 |
<=4.4 |
| 7000 |
3613 |
65.8 |
17.5 |
4.4 |
4.6 |
1.2 |
0.6 |
0.9 |
1.1 |
<=3.9 |
These experimental results have been explained precisely by the average-case
analysis of the GB Euclidean algorithm that has been undertaken
by Daireaux,
Maume-Deschamp
and Vallée, in their
article "The Lyapunov Tortoise and the Dyadic Hare".
Homepage