Journée en l'honneur de Georges Philibert

Michel Waldschmidt

(Prob. Diophantiens, Inst. de Math. de Jussieu, Univ. Paris 6)

Les cinq exponentielles plus ou moins une.

La conjecture des quatre exponentielles affirme que des nombres de la forme

$$(\log\alpha_1)(\log\alpha_4)-(\log\alpha_2) (\log\alpha_3),$$

avec des 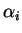$\alpha_i$ algébriques non nuls, ne s'annulent que dans des cas triviaux. Cela revient au même de dire que chacun des nombres

$${\log\alpha_1\over \log\alpha_2} - {\log\alpha_3\over\log\al... ...og\alpha_1)(\log\alpha_4)\over(\log\alpha_2)(\log\alpha_3)}-1,$$

n'est pas nul. On s'intéresse ici à la transcendance de ces nombres : si on admet la conjecture sur l'indépendance algébrique des logarithmes de nombres algébriques on peut affirmer que chacun de ces nombres est transcendant, en dehors de cas triviaux que l'on explicite facilement.

Si on n'admet pas cette conjecture, on peut démontrer des énoncés partiels dans le style du théorème des six exponentielles. Cela donne quatre énoncés ; pour trois d'entre eux on obtient la transcendance d'un nombre parmi deux, pour le dernier on obtient seulement la transcendance d'un nombre parmi quatre.

Retour à la page d'accueil.