The MOAIS/KAAPI Team have
successfully test the KAAPI library at the 3rd NQueens contest during the plugtest of the Grid@work event organized by ETSI, INRIA and CoreGRID.
The 4 key points of reaching this performance are :
-
1. have a simple API to develop parallel program. The program have been developed on top of the Athapascan API of KAAPI that defines only two keywords to describe parallelism. The first version was developed in less than half a day based on the original Takaken code. Three full-time days has been devoted to optimize the sequential code using C++ template specialization. The gain with the original Takaken code is about 34%. Optimized code is available with the KAAPI examples of the open source distribution here.
-
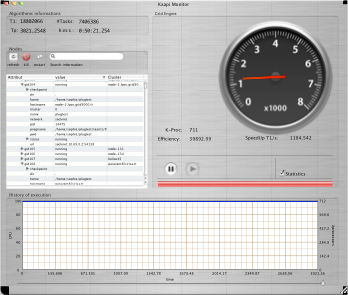
2.use a proved theoretical scheduling algorithm for these kind of strict multithreaded computation (our NQueens is a pure serie-parallel program) for both homogeneous or heterogeneous (in speed) clusters. This scheduling algorithm is basically a workstealing algorithm that is theoretically efficient for program with small critical path with respect to the work. Experiments during the contest have demonstrated its very good scalability up to 1458 processors.
-
3.use an efficient implementation of the workstealing algorithm. The KAAPI implementation takes care of the work-first principle that argues to move most of the extra instructions to handle the parallelism on the critical path rather than on the work. Moreover KAAPI implements a lock-free workstealing algorithm and its based on a light weight active message inter-process communication layer that allows dynamic message aggregation and it exhibits good overloading of communication by computation.
-
4.to finish, use parallel algorithms for most of the basic operation such as deployment of process onto machines. In KAAPI, we have port this deployment step on top of the TakTuk library. The result is here : in the same time required by other participants to deploy their application, our NQueens application 1/ is deployed and 2/ computes the solution of the NQueens N=22.