Gallery

• 
  • Examples of determinantal random subgraphs.

• ---

• 
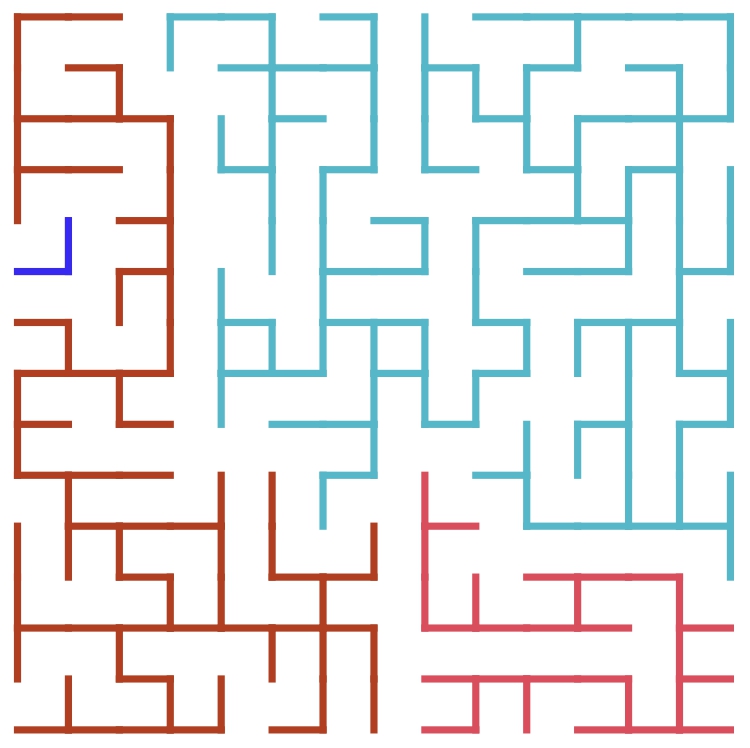
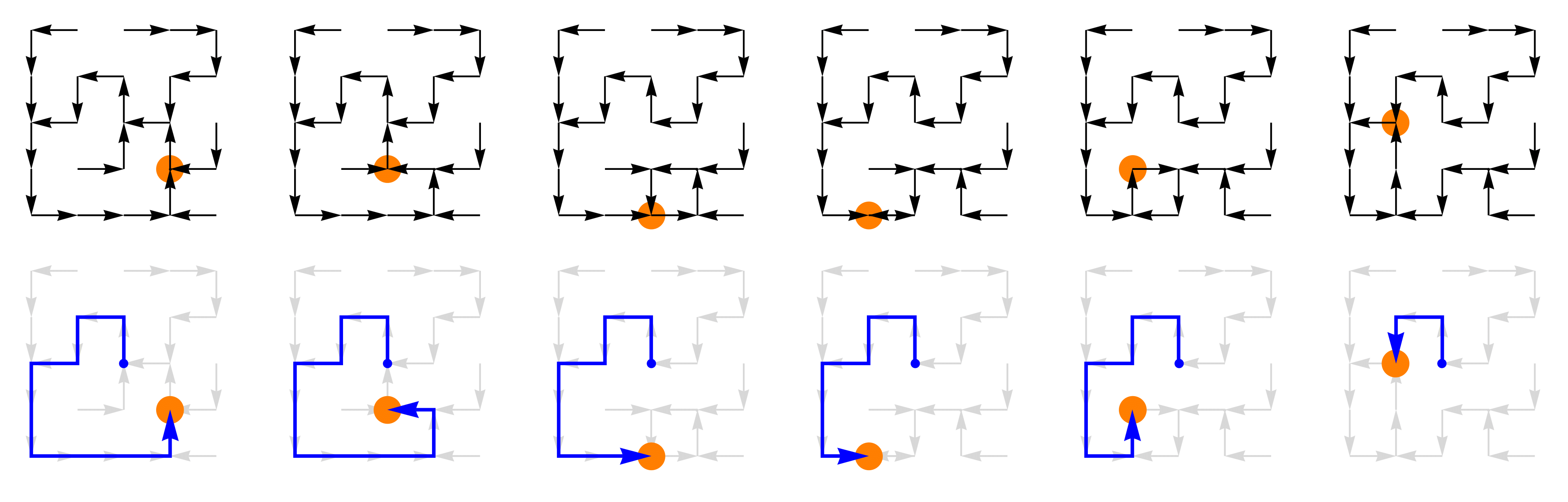
  • Top row: a rank 2 quantum spanning forest in a SU(2)–connection background on a square grid, represented here in an orthonormal basis.
    Bottom row: two independent samples of the associated Q-determinantal probability measure on cycle-rooted spanning forests (cycles are represented in boldface).
    The random {0,1,2}–valued fields of occupation number of the unions of subgraphs in each row have the same distribution, by Prop. 6.13 in the paper Determinantal probability measures on Grassmannians.

• ---

• 
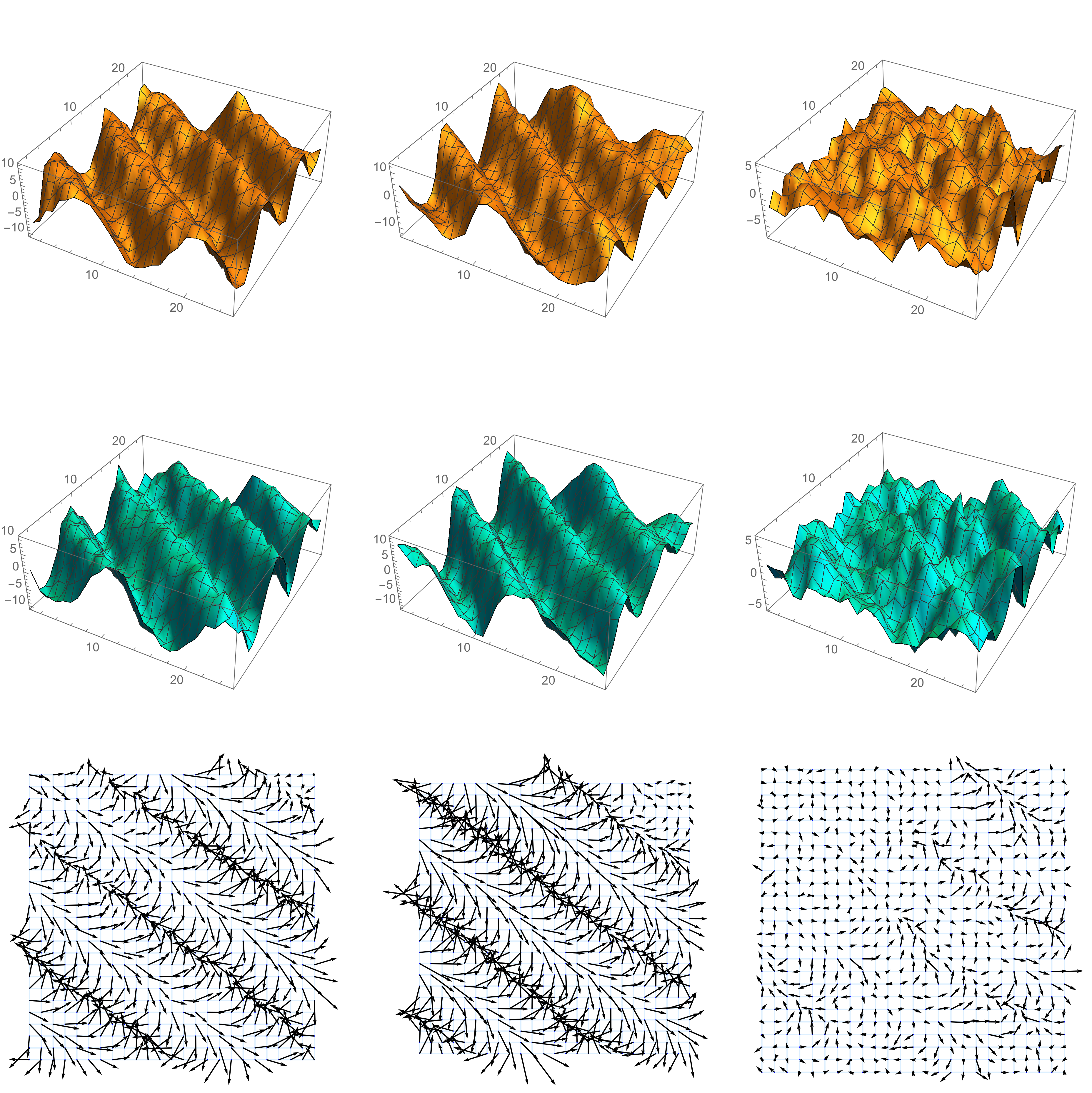
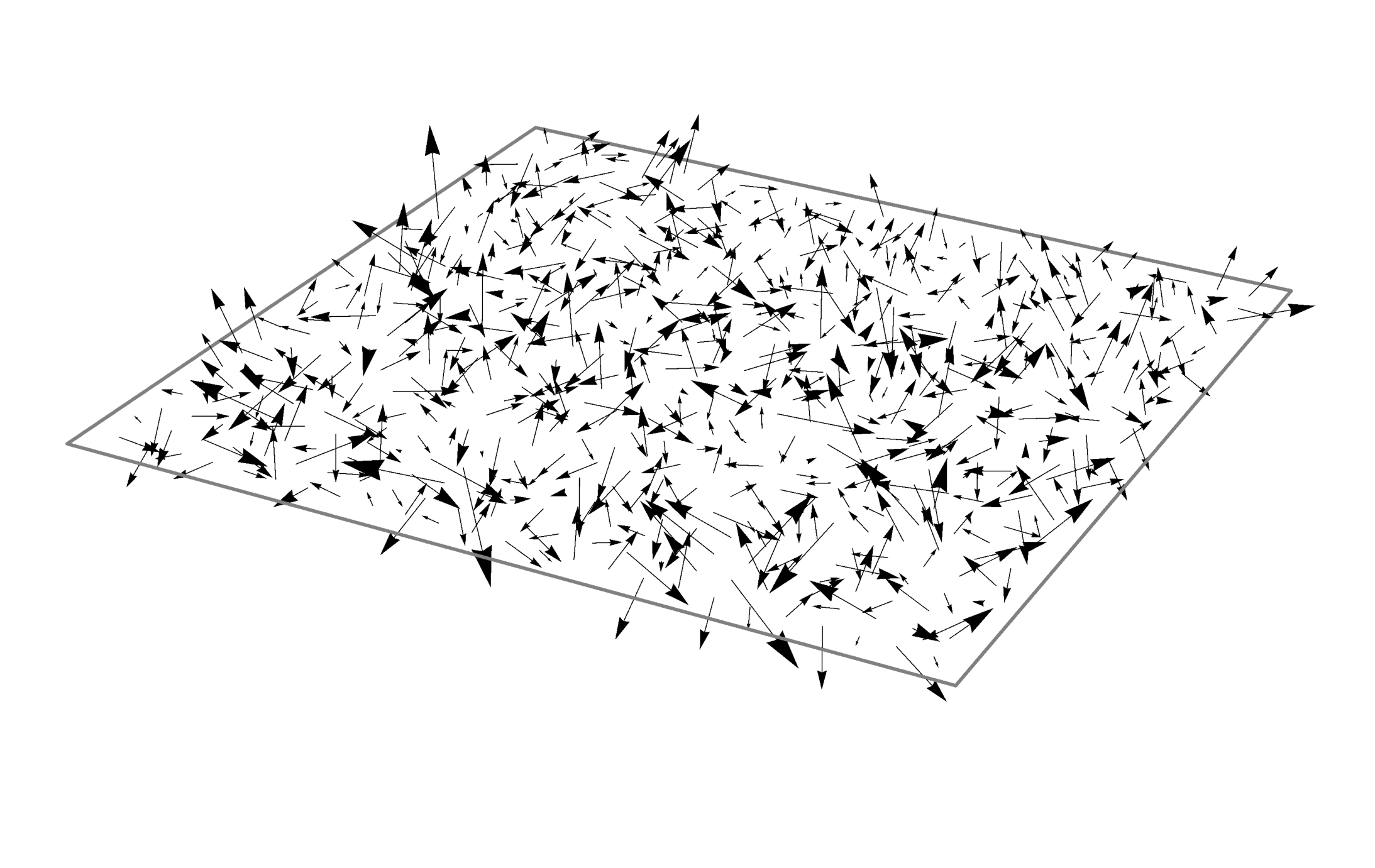
  • Three samples of a 2D, rank 2, discrete Gaussian free vector field and its two components in an orthonormal basis. See the paper Covariant Symanzik identities.

• ---

• 
  • A rank 3 quantum spanning forest in a SO(3) Yang–Mills background on a 2D square grid. This is an instance of a determinantal linear process. See Section 1.5 of the paper Determinantal probability measures on Grassmannians.

• ---

• 
  • A map decorated with a spanning tree can be represented as the gluing and quotient of two 1-dimensional graph plots.
    This allows to describe explicitely certain probability distributions on maps, like the ones decorated by a so-called active spanning tree
    (see the paper Active spanning trees and Schramm–Loewner evolution), and pass to a scaling limit.
    See the paper Active spanning trees with bending energy on planar maps and SLE–decorated Liouville quantum gravity for κ>8.

• ---

• 
  • A discrete Gaussian free vector field and its decomposition in an orthonormal basis. See the paper Covariant Symanzik identities.

• ---

• 
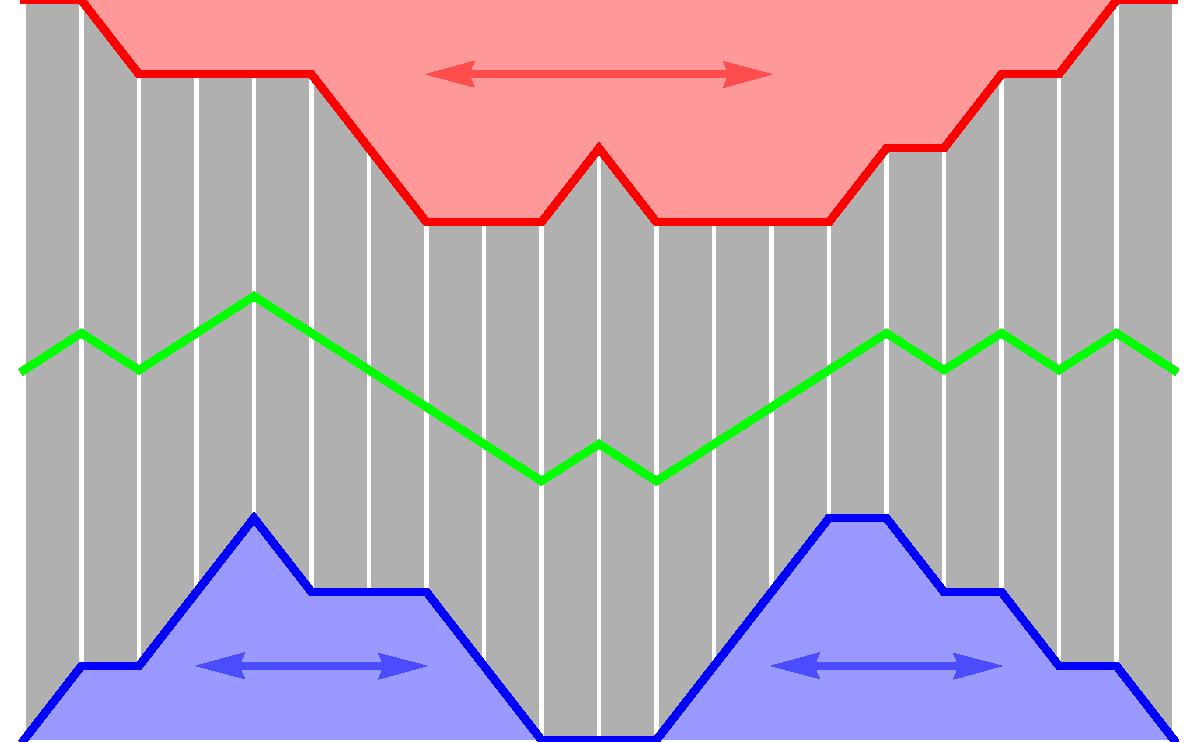
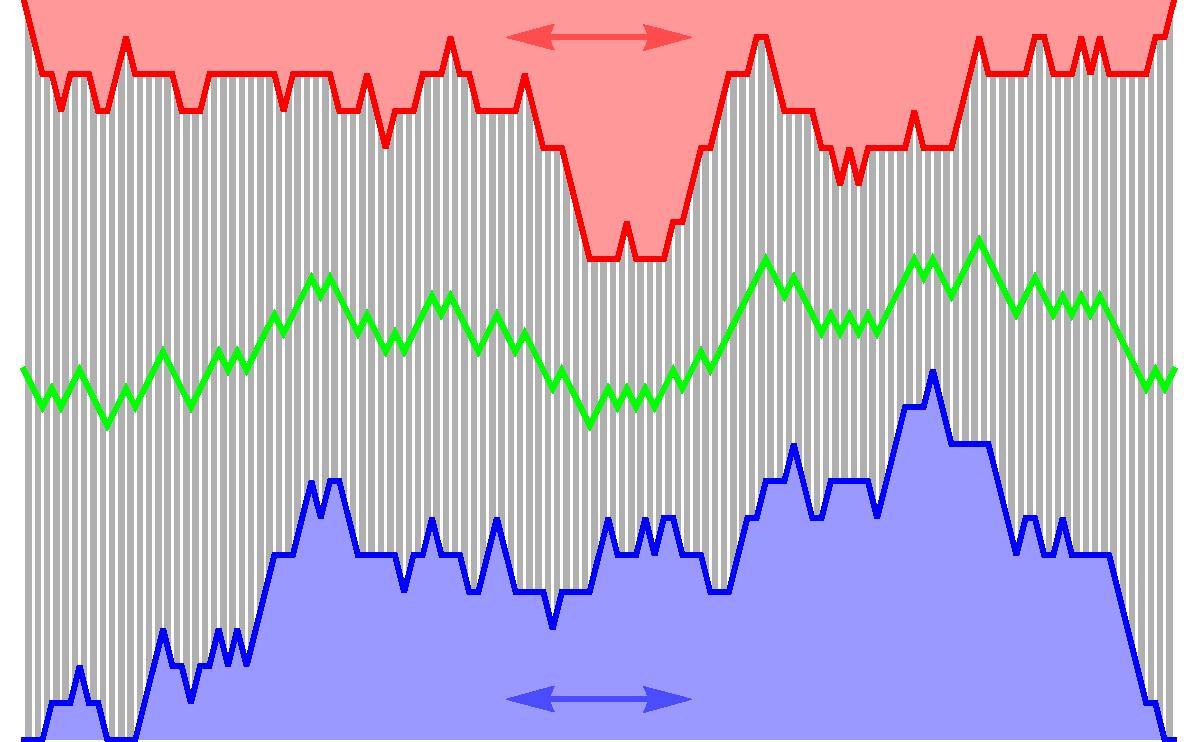
  • (Figure by David B. Wilson.) An active spanning tree is a random spanning tree of a graph whose probability depends exponentially on the number of its active edges (special edges determined by an exploration of the tree, represented by red dots in the Figure).
    When a high number of active edges is favored, this is in bijection with the Fortuin–Kasteleyn random cluster model, and expected (or known in some cases) to converge in 2D to branching SLE. When a small number of active edges is favored, we conjecture the scaling limit to be space-filling SLE.
    (When there is no dependency on the number of active edges, this is simply the uniform spanning tree which is known to converge to SLE.)
    See the paper Active spanning trees and Schramm–Loewner evolution for a definition, heuristics in favor of the conjecture, and computer simulations supporting it.

• ---

• 
  • A spanning unicycle with non-trivial topological type in a thrice punctured disk

• ---

• 
  • Spanning unicycle in an annulus

• ---

• 
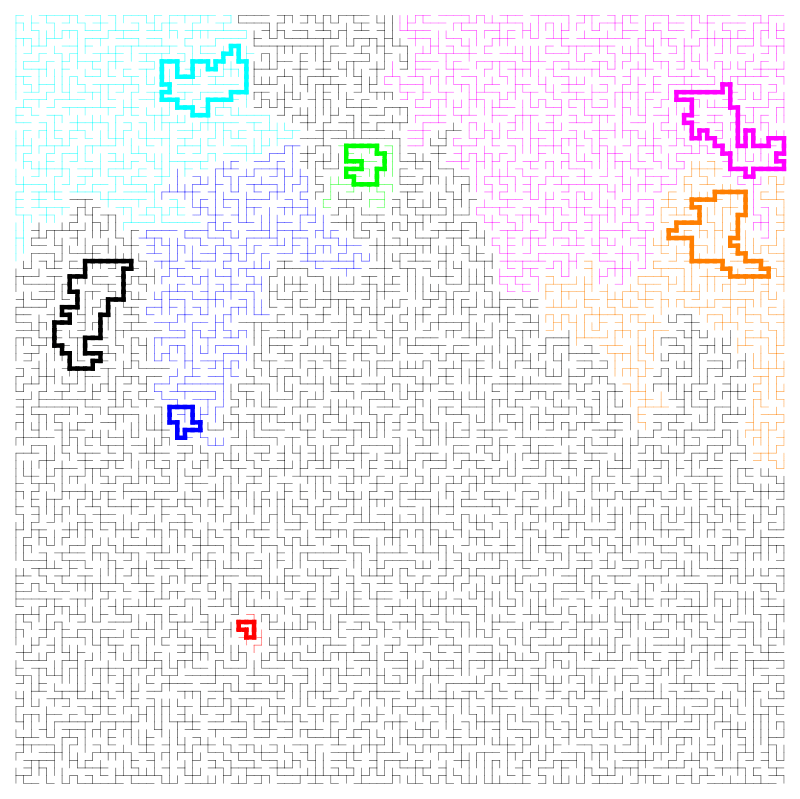
  • Cycle-rooted spanning forest of a square grid: each connected component is a unicycle

• ---

• 
  • The boundary of a uniform spanning tree in the 3D hypercubic lattice

• ---

• 
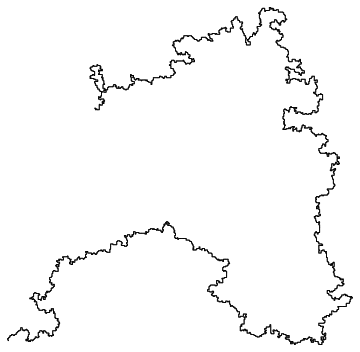
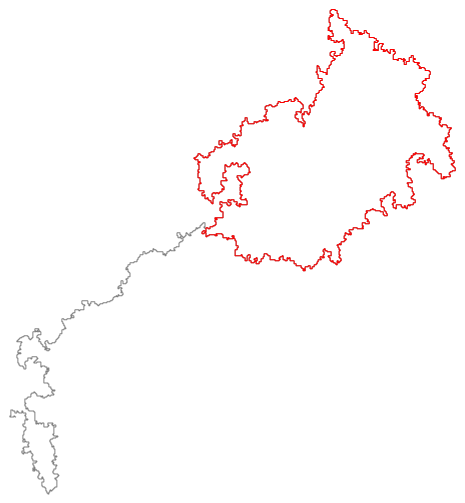
  • A loop-erased random walk approximating the Schramm–Loewner evolution

• ---

• 
  • Markov chain on spanning arborescences and its underlying loop-erased random walk. Length of loops erased on the square grid as a function of time.
    See the paper The looping rate and sandpile density of planar graphs.

• ---

• 
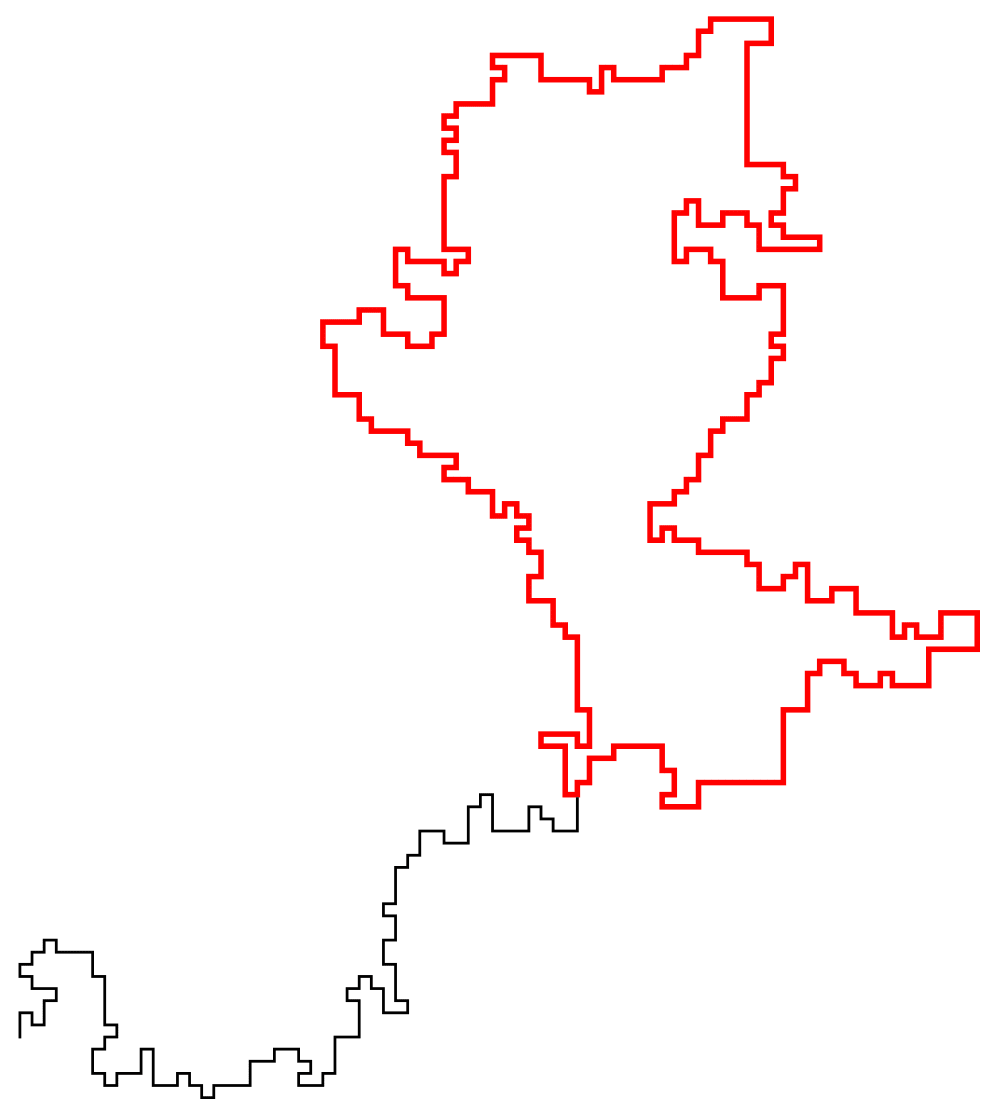
  • A lasso of loop-erased random walk

• ---

• 
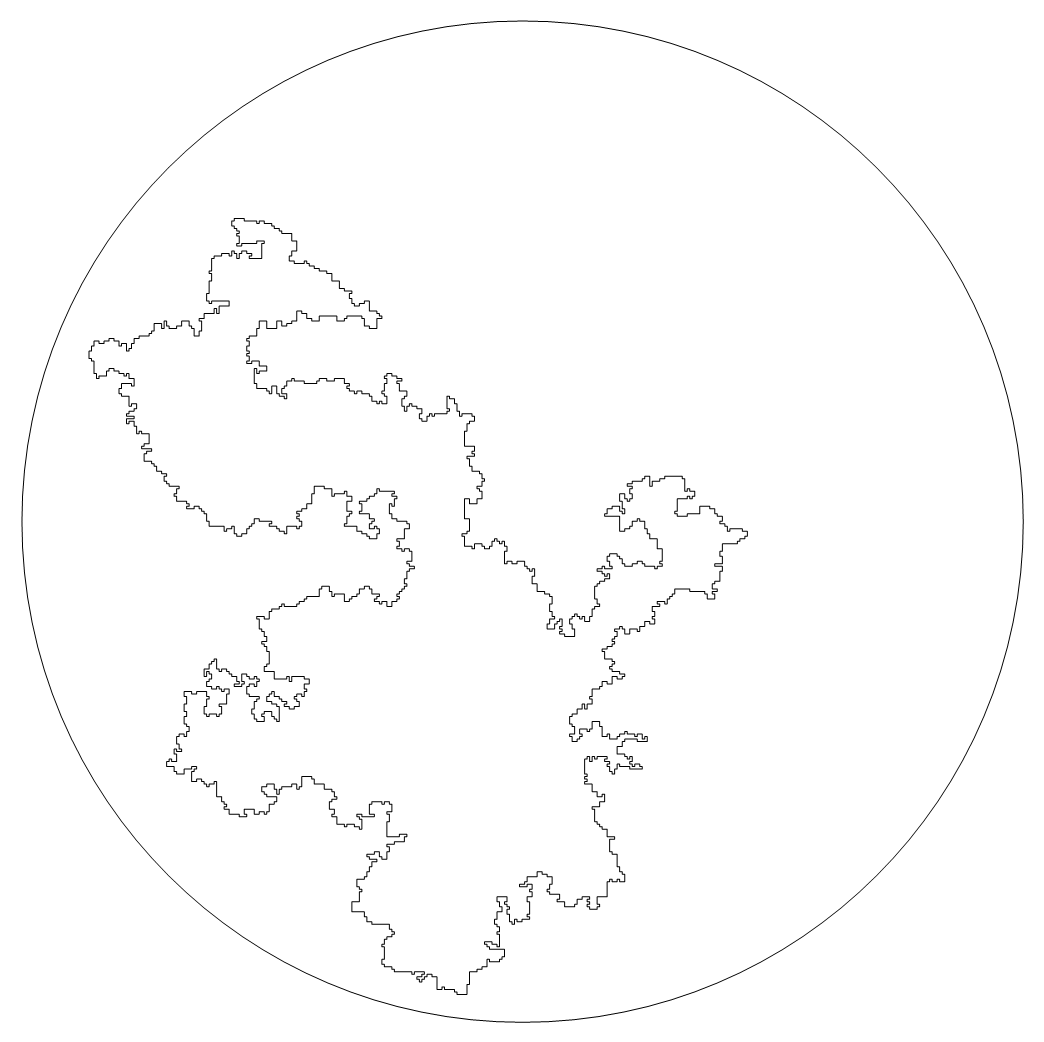
  • A random loop in the hyperbolic disk

• ---

• 
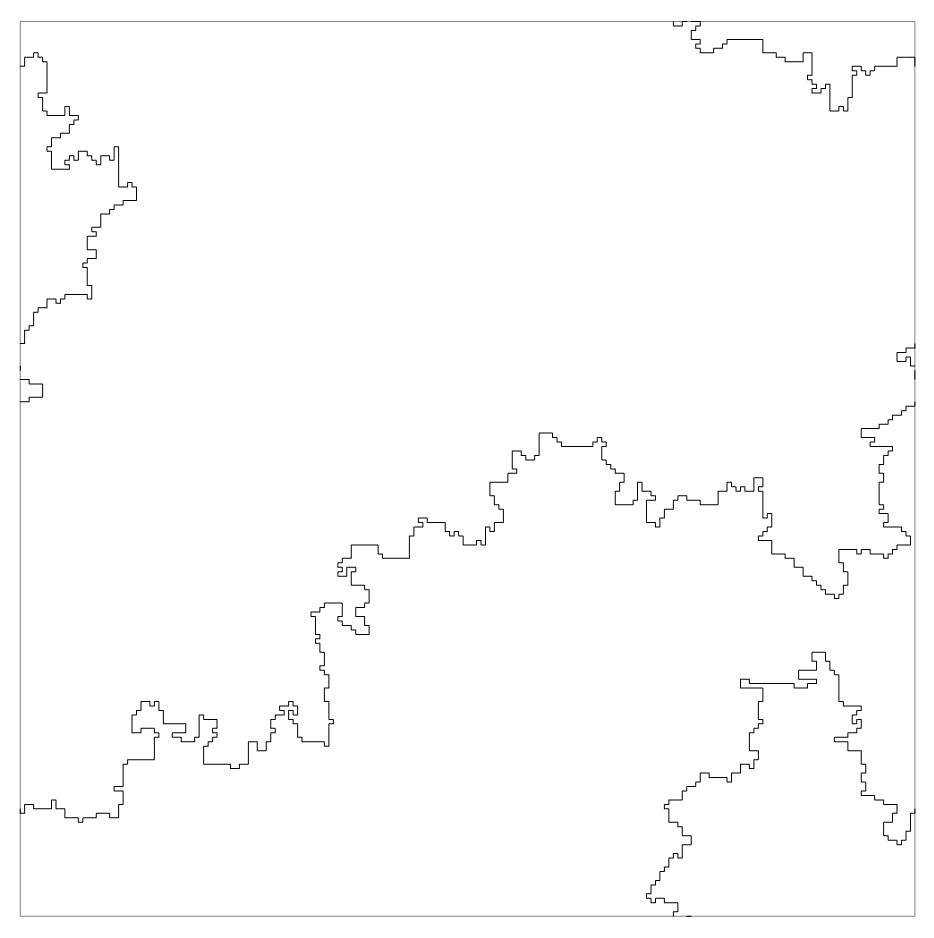
  • A random loop on a flat torus

• ---

• 
  • Loops on curved surfaces. See the paper Random curves on surfaces induced from the Laplacian determinant.

• ---

• 
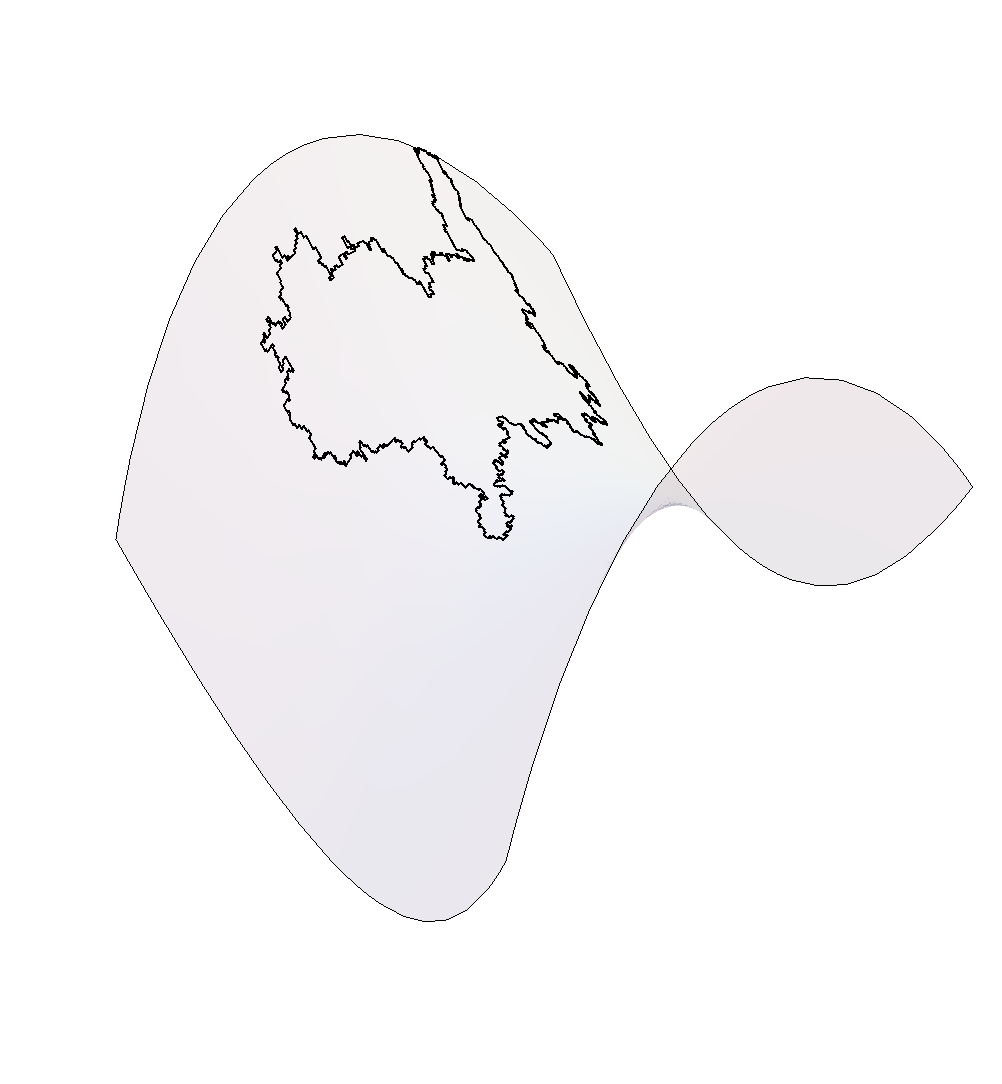
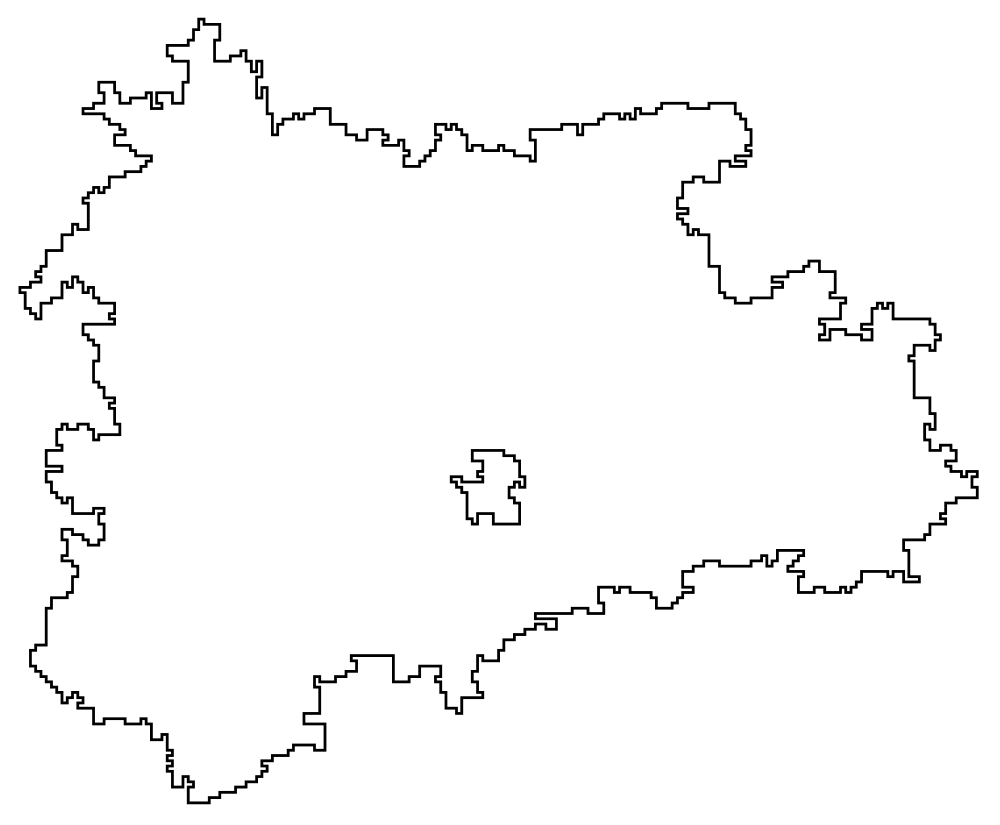
  • Two nested random loops in the plane

• ---

• 
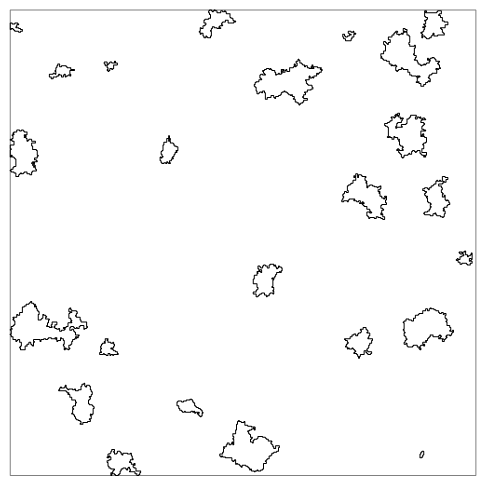
  • A cloud of random loops in the plane

• ---

• 
  • A random spanning forest

• ---

• 
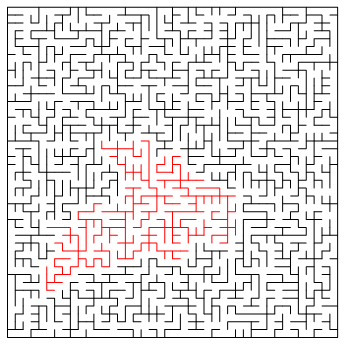
  • A two-component spanning forest

• ---

• 
  • A uniform spanning tree

• ---

• 
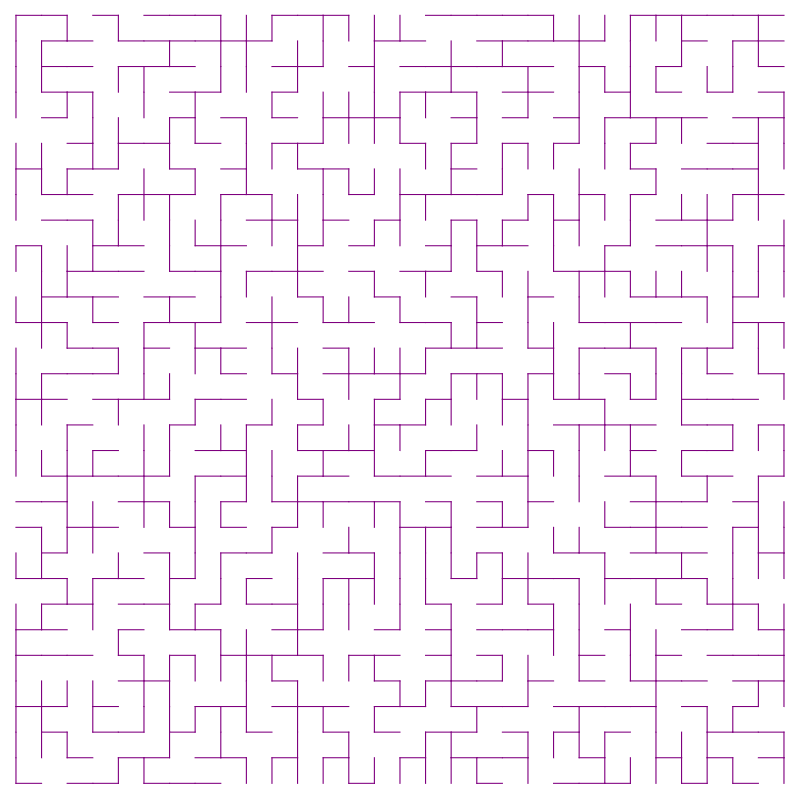
  • Sandpile stabilization illustrated. Stabilization of a large pile of chips located at the origin of the square grid.

• ---

• 
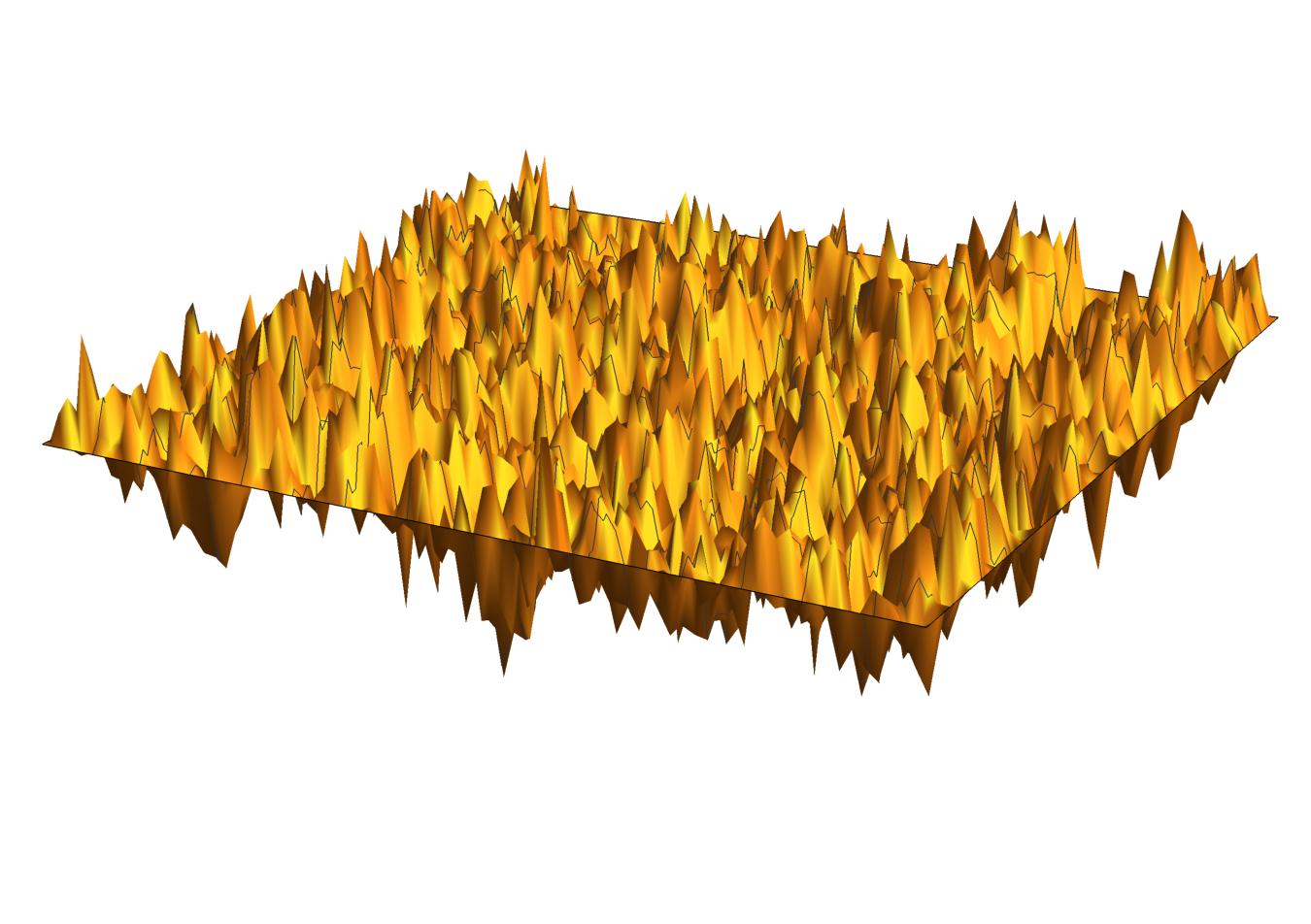
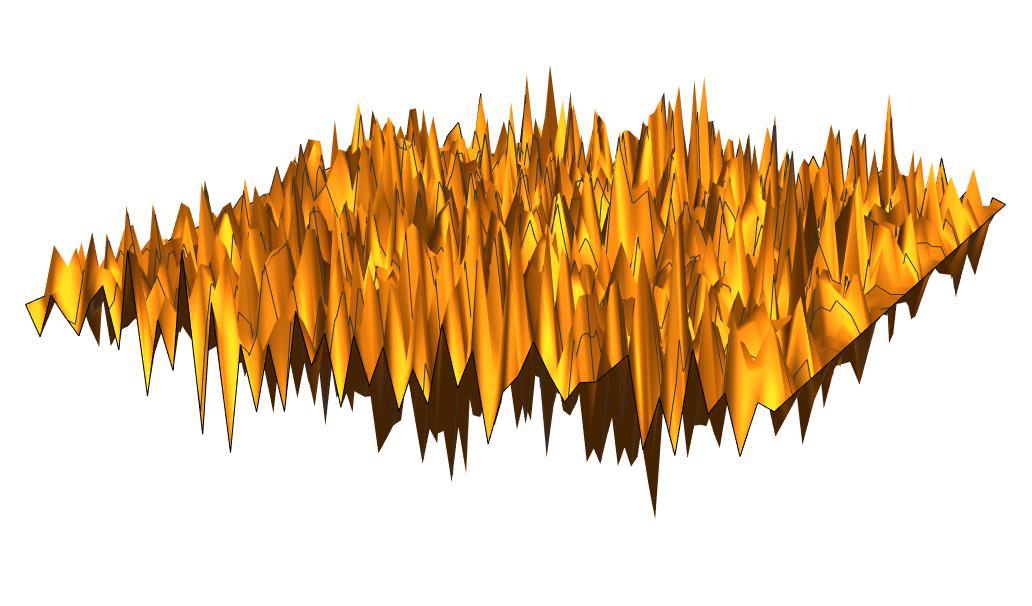
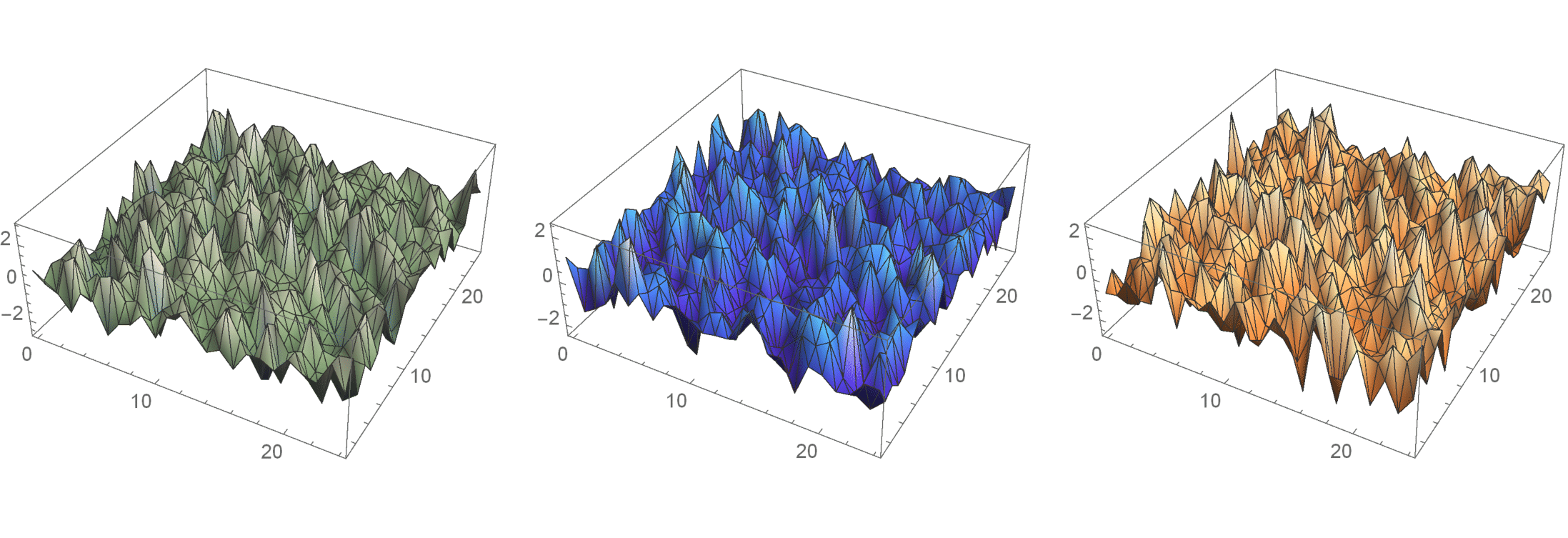
  • A discrete Gaussian free field, with zero boundary conditions, periodic boundary conditions (on a torus), and mixed boundary conditions (on a cylinder).
    This is the discrete grid approximation of the most natural fluctuations of a surface around the flat equilibrium position.

• ---

[Back to main page]