You can find implementations of some of the methods I developed during my research on this page.
These codes are primarily written using Matlab,
with a bit of FreeFem++ in 3D,
and I also sometimes use a finite element solver developed by L. Seppecher.
Do not hesitate to write to me with any questions about these codes.
I also put on this page some Asymptote codes to generates 3D schemes of waveguides and plates.
I also put on this page some Asymptote codes to generates 3D schemes of waveguides and plates.
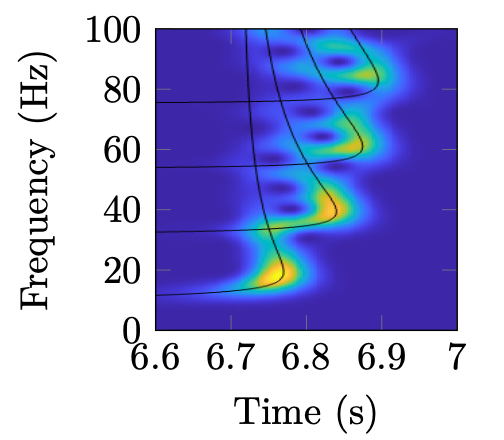Spectrogram of a received signal in a Pekeris waveguide.
Source localisation in shallow water
You can find here
different codes to recover in a completely automated way the location of sources in shallow water using the received signal measured
in one point. The method uses the following elements:
➤ First, we use an optimised warping to separate each modal component
➤ Then, we recover the dispersion curves with an optimised maximum method
➤ Finally, we implement a penalized minimization algorithm to recover the location of the source
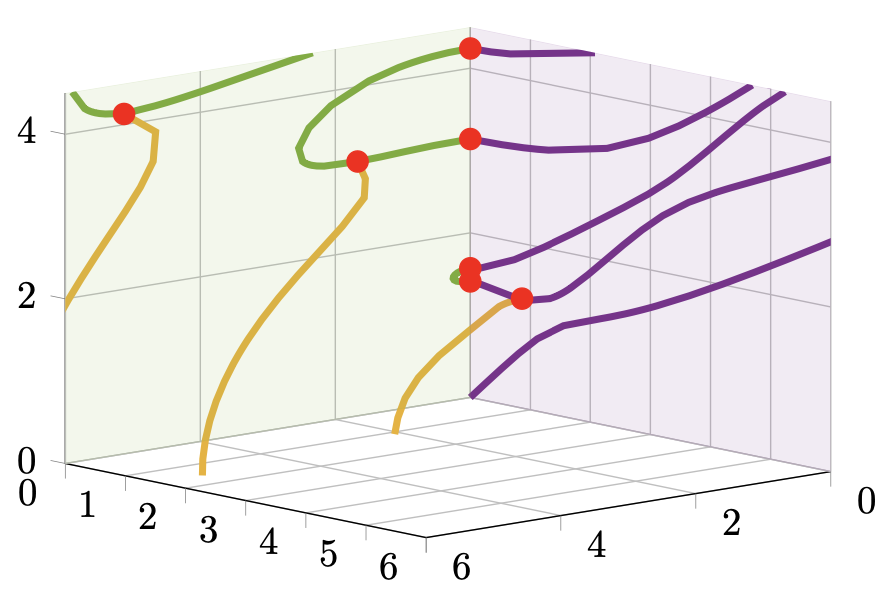Rayleigh-Lamb dispersion curves
Lamb modes
You can find here different codes to
generate a 3D view of the Rayleigh-Lamb dispersion curves of an elastic plate.
You can also use them to create symmetric and antisymmetric Lamb modes schemes.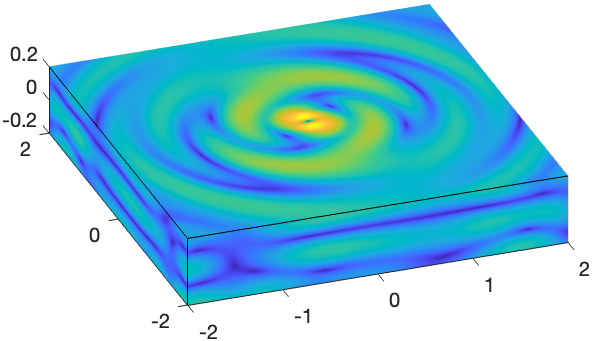 
Longitudinal displacement of an elastic wave propagating in a thick infinite 3D plate
Elastic waves in 3D plates
You can find here different codes for
numerical simulations of elastic wavefields in 2D waveguides and 3D plates given general internal and boundary source terms.
I present two ways to obtain such results (see more details in my research paper [6]):
➤ Using finite elements, PML's and
a post-processing to handle backward modes
➤ Using a 3D Lamb-SH modal decomposition computed using 2D-convolutions
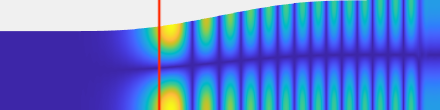
Wavefield in a 2D acoustic waveguide at locally resonant frequencies. In red, we represent the locally resonant coordinate.
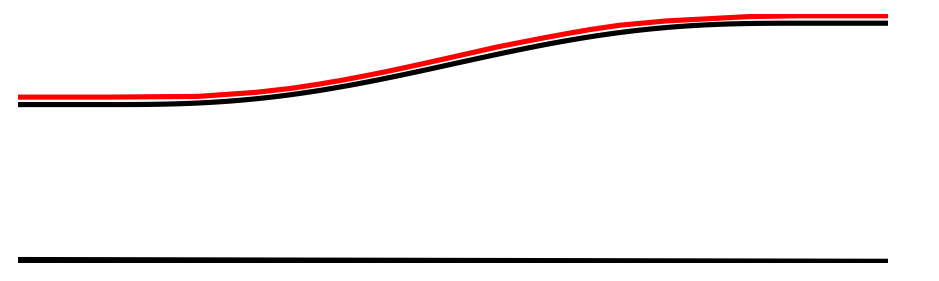
Black: initial shape defect. Red: reconstruction of the shape defect slightly shifted for comparisons.
Local resonances in 2D acoustic waveguides
You can find here different codes to
get numerical simulations of acoustic waveguides excited at locally resonant frequencies. These data are then used to obtain reconstructions of shape defects
(see more details in my research papers [5,8]). Data for the forward problem can be generated using two different methods:
➤ Using finite elements and PML's
➤ Using a modal decomposition with modified Airy functions computed using 1D-convolutions
Initial inhomogeneity in a 2D waveguide
Reconstruction using the multifrequency scattering method
Multifrequency one-side scattering inversion
You can find here different codes to
recover inhomogeneities, shape defects and bends in 2D and 3D acoustic waveguides using a multifrequency one-side
scattering inversion (see more details in my research paper [4]). To avoid doing an "inverse crime", we use two different methods to
generate data and inverse the problem:
➤ Data for the forward problem are generated using finite elements and PML's
➤ The inversion is performed using a penalized Tikhonov least square algorithm
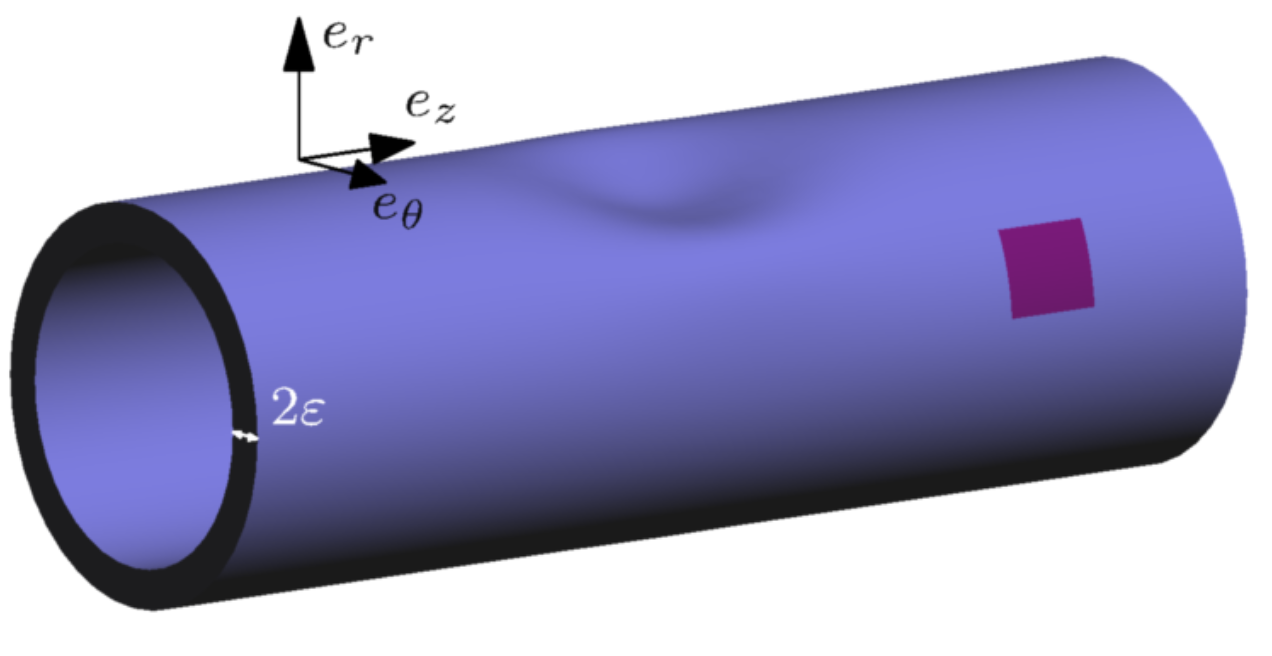
Scheme of a 3D waveguide with a shape defect
3D plates and waveguides scheme
You can find here different codes to
generate 3D schemes of plates and waveguides with defects.