
Très régulièrement, dans le cadre de ma mission de support à la recherche, on me demande de réaliser (ou d’aider à réaliser) des ACP (Analyses en Composantes Principales). En général cette demande ne s’ensuit pas d’un fol enthousiasme de ma part: je me sens un peu comme une cuisinière “bistronomique” à qui on demanderait tout le temps une entrecôte-frites. Je peux comprendre le côté “tradi mais appétent” mais pour moi c’est pas l’éclate.
Quoi qu’il en soit, la demande étant somme toute légitime (et fréquente) voici un billet où je rassemble quelques éléments d’information et outils pour réaliser des ACP sans douleur.
Une ACP, pour quoi faire
Une ACP (ou “PCA” pour Principal Components Analysis en anglais) c’est une analyse qui vise à décrire un jeu de données comprenant de multiples variables quantitatives.
Elle fait partie d’une même “famille” d’analyses, celle des analyses factorielles qui s’appliquent à de larges tableaux de données (pas forcément uniquement composés de variables quantitatives comme dans le cas de l’ACP).
Le principe d’une ACP est de réduire un jeu de données à N>2 variables (i.e. N dimensions) à quelques (généralement 2) variables nouvelles (ce qu’on appelle les composantes principales). Le but de la manoeuvre, c’est d’obtenir quelque chose qui est beaucoup plus facile à décrire et à représenter qu’un jeu de données avec beaucoup de variables (puisque 2 dimensions, c’est ce qu’il faut pour représenter le jeu de données “dans son entièreté” sur un graphique, que ce soit pour un article papier ou sur un écran d’ordinateur…).
Le coeur du “job” de l’ACP, c’est donc justement de calculer ces composantes principales à partir des variables de base.
Tentons une analogie.
Imaginez une banane par exemple. Il s’agit d’un objet 3D. Si je veux le représenter en 2D, selon l’angle que je choisirai pour la représenter, je vais obtenir quelque chose de plus ou moins “reconnaissable”.

A gauche, l’angle choisi est tel qu’on ne reconnaît pas la forme de la banane. A droite, c’est bien mieux, car l’angle choisi permet de reconnaître le côté allongé et courbé caractéristique. Notez que dans les deux cas, la couleur est une information supplémentaire bienvenue pour l’interprétation ;-)..
Eh bien, pour réaliser l’image de droite, un dessinateur fait un peu l’équivalent d’une ACP en trouvant un “angle” (ou plus précisément un “plan” défini par deux axes) qui va apporter le plus d’information possible sur l’objet, de sorte que l’oeil humain puisse interpréter de quoi il s’agit.
Quand on travaille sur un jeu de données à N>>2 dimensions (et généralement N>>3) il est évidemment plus difficile d’avoir une image mentale de la structure/forme de l’objet d’origine que dans le cas d’une banane… La représentation “la plus juste possible” de cet objet en 1D, 2D ou 3D que propose l’ACP va permettre d’appréhender cette structure/forme.
Calcul des composantes principales
Je ne rentrerai pas ici dans le détail du calcul réalisé dans le cadre d’une ACP. Il y a derrière des notions de maths qui ne sont pas forcément très accessibles (c’est selon votre sensibilité, votre cursus, et la fraîcheur de vos études mais par exemple, j’ai pour ma part fait une prépa bio/véto il y a une quinzaine d’années -et donc pas mal de maths- mais le mécanisme exact du calcul me semble toujours un peu difficile à appréhender!).
Néanmoins, si vous êtes frustrés de ne pas comprendre “en profondeur” la méthode et que vous pensez que cela nuit à la qualité des interprétations que vous faites de vos analyses factorielles, je recommande les matériels pédagogiques relatifs au package FactoMineR, et en particulier pour les ACP en particulier cette vidéo de François Husson, un des auteurs du package. C’est très bien amené et expliqué! Si vous tombez au bon moment, vous pouvez même suivre le MOOC (je l’ai suivi moi-même il y a quelques années et cela m’a bien aidé à mettre mes idées au clair).
Réaliser l’ACP
Il existe plusieurs packages pour réaliser les ACP. Les deux principaux, FactoMineR et ade4 ont été développés par des équipes françaises (cocorico!🐓). Et ce n’est guère surprenant, les analyses factorielles elles-mêmes étant très françaises (comme l’entrecôte-frites?) puisqu’elles ont été mises au point dans les années 70 notamment par un certain Jean-Paul Benzécri et par son équipe.
Le package ade4 a été développé (et est maintenu) par une équipe lyonnaise, qui travaille notamment avec des biologistes de l’évolution et des écologues (cela se ressent sur les exemples d’application d’ACP avec ce package que vous pourrez trouver!). Le package FactoMineR a quant à lui été développé (et est maintenu) par une équipe rennaise, qui travaille dans un univers un peu plus “agronomique”. Pour les méthodes les plus centrales (ACP, AFC), les différences entre ces packages sont à mon avis mineures et une fois que vous avez compris le principe d’une ACP vous pouvez sans inconvénient majeur opter pour l’un ou l’autre. Pour ma part, bien que Lyonnaise, j’ai une petite préférence pour FactoMineR car je trouve que c’est un peu plus facile de s’y retrouver (que ce soit pour les noms des fonctions ou des objets renvoyés, ou pour les supports pédagogiques).
Du coup, pour vous montrer un exemple d’ACP, je vais partir sur un exemple avec FactoMineR. D’ailleurs, je ne me casse vraiment pas la tête ici puisque je reprends le jeu de données et l’exemple proposé sur le site de FactoMineR lui-même
library(FactoMineR)
data(decathlon)
head(decathlon)
## 100m Long.jump Shot.put High.jump 400m 110m.hurdle Discus Pole.vault Javeline 1500m Rank Points Competition
## SEBRLE 11.04 7.58 14.83 2.07 49.81 14.69 43.75 5.02 63.19 291.7 1 8217 Decastar
## CLAY 10.76 7.40 14.26 1.86 49.37 14.05 50.72 4.92 60.15 301.5 2 8122 Decastar
## KARPOV 11.02 7.30 14.77 2.04 48.37 14.09 48.95 4.92 50.31 300.2 3 8099 Decastar
## BERNARD 11.02 7.23 14.25 1.92 48.93 14.99 40.87 5.32 62.77 280.1 4 8067 Decastar
## YURKOV 11.34 7.09 15.19 2.10 50.42 15.31 46.26 4.72 63.44 276.4 5 8036 Decastar
## WARNERS 11.11 7.60 14.31 1.98 48.68 14.23 41.10 4.92 51.77 278.1 6 8030 Decastar
Il s’agit donc d’un jeu de données qui comprend les résultats pour différentes épreuves du Décathlon (en colonnes) de plusieurs athlètes (en lignes).
Les 10 premières colonnes correspondent aux résultats (quantitatifs) aux 10 épreuves du Décathlon. Attention, pour les épreuves de vitesse (100m, 110m.hurdle, 400m, 1500m), les valeurs élevées correspondent à de mauvaises performances!… Les variables supplémentaires “Rank”, et “Points” correspondent respectivement aux rang, et nombre de points total de chaque athlète, La variable supplémentaire “Competition” indique lors de quelle compétition ces résultats ont été obtenus.
Réalisons une ACP sur les 10 premières variables (les variables quantitatives) pour avoir un “aperçu” de la structure des résultats des athlètes aux différentes épreuves. J’utilise pour ce faire une fonction qui s’appelle PCA():
resultat=PCA(decathlon[,1:10], graph=FALSE)
Et voilà! ça tourne en une demi-seconde, et renvoie (en plus de graphiques si on ne précise pas graph=FALSE) le résultat suivant.
resultat
## **Results for the Principal Component Analysis (PCA)**
## The analysis was performed on 41 individuals, described by 10 variables
## *The results are available in the following objects:
##
## name description
## 1 "$eig" "eigenvalues"
## 2 "$var" "results for the variables"
## 3 "$var$coord" "coord. for the variables"
## 4 "$var$cor" "correlations variables - dimensions"
## 5 "$var$cos2" "cos2 for the variables"
## 6 "$var$contrib" "contributions of the variables"
## 7 "$ind" "results for the individuals"
## 8 "$ind$coord" "coord. for the individuals"
## 9 "$ind$cos2" "cos2 for the individuals"
## 10 "$ind$contrib" "contributions of the individuals"
## 11 "$call" "summary statistics"
## 12 "$call$centre" "mean of the variables"
## 13 "$call$ecart.type" "standard error of the variables"
## 14 "$call$row.w" "weights for the individuals"
## 15 "$call$col.w" "weights for the variables"
Ce résultat comprend 3 éléments principaux:
-
eigdes infos sur leseigenvalues(ou “valeurs propres”), qui vont nous permettre d’évaluer la qualité de l’ACP. J’y reviendrai dans la partie suivante. -
ind: des infos sur les individus (lignes du tableau initial) -
var: des infos sur les variables (colonnes du tableau initial)
ind et var contiennent tous deux des éléments d’information correspondant à
-
coordles coordonnées des individus ou variables sur les axes principaux -
cos2qui permet d’évaluer si un individu ou une variable en particulier est bien représenté sur les axes principaux -
contribqui permet d’évaluer le “poids” d’un individu ou d’une variable particuliers dans le calcul des axes.
Les résultats graphiques d’une ACP correspondent usuellement à la représentation des coordonnées des individus et des variables dans l’espace défini par les axes principaux (en pratique, on en retient souvent 2 par défaut). C’est le cas ici, si on laisse FactoMineR nous proposer une représentation graphique de l’ACP (en ne précisant pas graph=FALSE).
resultat=PCA(decathlon[,1:10])
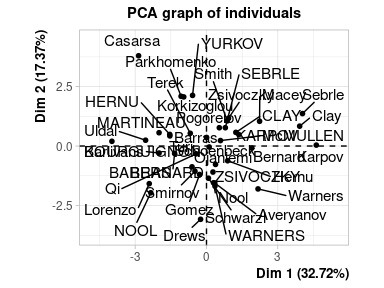
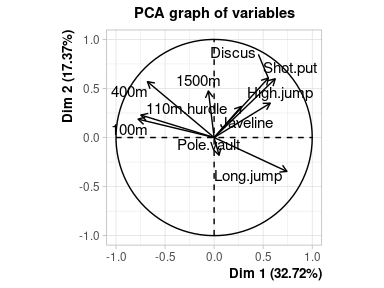
Le premier graphique correspond aux individus, le deuxième aux variables.
Ces deux représentations sont (rappelons-le) imparfaites puisqu’en réduisant le nombre de dimensions du jeu de données de 10 à 2 on a perdu une partie de l’information contenue par le jeu de données.
Qualité de l’ACP
Les eigenvalues apportent une information quant à la qualité de l’ACP en permettant de calculer la proportion de variance (ou inertie) du jeu de donnée initial qui est portée par les composantes principales issues de l’analyse.
resultat$eig
## eigenvalue percentage of variance cumulative percentage of variance
## comp 1 3.2719055 32.719055 32.71906
## comp 2 1.7371310 17.371310 50.09037
## comp 3 1.4049167 14.049167 64.13953
## comp 4 1.0568504 10.568504 74.70804
## comp 5 0.6847735 6.847735 81.55577
## comp 6 0.5992687 5.992687 87.54846
## comp 7 0.4512353 4.512353 92.06081
## comp 8 0.3968766 3.968766 96.02958
## comp 9 0.2148149 2.148149 98.17773
## comp 10 0.1822275 1.822275 100.00000
Par construction, l’ACP calcule et ordonne les composantes pour que la première porte plus d’information que la deuxième, qui en porte plus que la troisième, etc.
Les valeurs dans la deuxième colonne (percentage of variance) correspondent en effet aux valeurs d’eigenvalues divisées par le nombre initial de variables (10).
On retrouve dans cette colonne percentage of variance les valeurs de 32.72% et 17.37% qui étaient indiquées dans les étiquettes d’axes des deux graphiques ci-dessus. Ainsi, avec une représentation 2D (correspondant aux deux premiers axes principaux) on arrive à représenter 32.7+17.3=50.0% de l’information contenue dans le jeu de données initial.
*"Et alors, __% d’inertie portée par mes deux premiers axes, c’est bien ou c’est pas bien?"* m’entends-je demander parfois.
Eh bien mon bon monsieur, ma bonne dame, ptêt ben qu’oui, ptêt ben qu’non. Il n’existe à ma connaissance pas de convention sur une valeur qui serait “suffisamment bonne”.
Ici, on a 50% de l’info sur 2 axes, alors qu’on avait 10 variables à la base. Avant de réaliser l’ACP, deux dimensions correspondaient donc à 2 fois un dixième de l’inertie du jeu de données, soit 20%. L’ACP a donc permis de passer de 20% à 50% de l’info représentable par un graphique 2D: ça semble honnête, tant qu’on garde à l’esprit dans les interprétations que la moitié de l’info est perdue dans notre tentative de simplification.
Si on avait eu à la base 4 variables dans le jeu de données, 50% de l’info représentée par les deux premiers axes de l’ACP, ç’aurait été clairement très mauvais, puisque 2 sur 4 des variables initiales auraient déjà pu apporter cette part d’info. Autrement dit, l’ACP n’aurait servi à strictement rien.
La proportion d’info portée par les composantes principales dépend évidemment du nombre de variables en entrée.
Mais pas que.
Ce qui permet à l’ACP de “réduire en dimensionnalité” un jeu de données, c’est l’existence de corrélations entre les variables d’origine.
Si dans un jeu de données on a deux groupes de variables extrêmement inter-corrélées, alors très bien: deux composantes principales seront à même de représenter relativement bien les deux types d’effets. Si en revanche les N>>2 variables sont très peu corrélées les unes aux autres, alors on n’a aucune chance de “résumer” fidèlement le jeu de données dans son ensemble à l’aide de quelques composantes principales…
Interprétation
On peut interpréter les sorties graphiques d’une ACP de trois manières:
- en examinant la position des variables dans le nouveau repère (et en comparant la position des variables les unes par rapport aux autres)
- en examinant la position des individus dans le nouveau repère (et en comparant la position des individus les uns par rapport aux autres)
- en examinant la position des individus par rapport à la position des variables dans le nouveau repère
Position des variables
La représentation des variables dans le plan factoriel, aussi appelé cercle des corrélations, permet d’évaluer la liaison entre les variables.
Plus l’angle entre deux variables est petit, plus la corrélation est proche de 1. Si l’angle est droit, la corrélation est proche de 0. Si l’angle est de 180° (les flèches sont opposées) alors la corrélation est proche de -1. tout ça est s’applique évidemment si les variables sont “bien représentées” par les deux premiers axes de l’ACP
plot.PCA(resultat, choix="var")
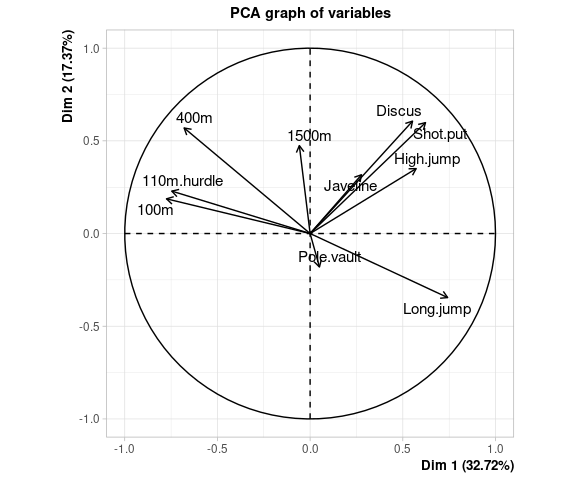
Ici par exemple, les performances des sportifs semblent corrélées positivement pour les disciplines de “force” Discus,Shot.put,High.jump. Les disciplines de “vitesse” 400m, 110m.hurdle 100m sont aussi positivement corrélées les unes aux autres. La performance en Long.jump est inversement corrélée aux résultats de vitesse (rappelons que les résultats de vitesse sont des temps, donc une bonne performance sur les épreuves de vitesse est corrélée à une bonne performance en saut en longueur).
La qualité de représentation d’une variable par un axe peut être évaluée à travers le cosinus carré de l’angle entre la variable et l’axe considéré. Le cosinus correspond à la projection orthogonale de la pointe de la flèche sur l’axe. Du coup, (petit rappel du théorème de Pythagore) la qualité de représentation sur les deux axes (i.e. la somme des cosinus carrés) correspond à la longueur de la flèche: plus la pointe de la flèche est proche du cercle, plus la représentation de la variable dans le plan factoriel est “de qualité”.
Rappelons que le premier axe correspond à la plus grande part d’inertie du jeu de données initial. Ici, on voit que le jeu de données est structuré principalement par (à droite) les bonnes performances (i.e. petites valeurs pour les épreuves de vitesse et grosses valeurs pour toutes les autres) vs (à gauche) les mauvaises performances.
Position des individus
plot.PCA(resultat, choix="ind")
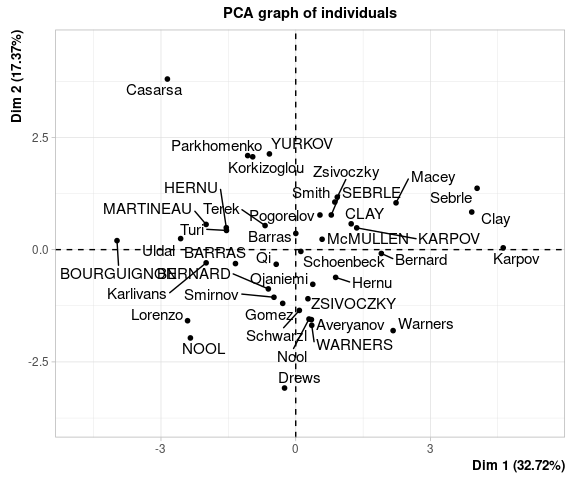
Ce graphique montre les “ressemblances” entre individus. Plus ils sont proches (comme par exemple Parkhomenko et Korkizoglou, en haut à gauche, ou Karpov, Sebrle et Clay à droite), et plus leurs “profils” de performance sont vraisemblablement similaires.
Les coordonnées des individus peuvent ainsi classiquement servir de base pour définir des classes d’individus à travers une classification hiérarchique ascendante (par exemple).
Comme dans le cas des variables, les individus les mieux représentés par le plan factoriel sont ceux les plus éloignés du centre (même si ici on ne peut pas lire directement les valeurs de cosinus sur le graphique - elles sont en revanche disponible dans l’objet resultat issu de l’ACP).
La position des individus peut en outre être interprétée en lien avec la position des variables. Par exemple Casarsa, tout en haut à gauche, a vraisemblablement eu des résultats assez mauvais dans toutes les épreuves, tandis que Sebrle (à droite, en haut) a plutôt eu de bons résultats, en particulier dans les épreuves “de force”.
Représentations graphiques
Pour l’instant je me suis contentée d’utiliser les représentations graphiques proposées par le package FactoMineR lui-même. Elles peuvent être suffisantes pour une première exploration des résultats d’ACP mais ne suffisent généralement pas à produire des graphiques suffisemment lisibles et jolis pour (par exemple) faire partie d’articles, rapports ou autres.
Il existe divers packages qui permettent d’améliorer et paramétrer finement les graphiques typiques d’une ACP. Si vous travaillez avec le package FactoMineR, le package factoextra est une possibilité intéressante. Voyez ici très bien fait qui vous montrera quelques exemples d’utilisation de ce package (Vous ne serez de plus pas trop perdus car ce billet utilise aussi des données d’exemple liées au Décathlon -attention tout-de-même il s’agit d’un jeu de données decathlon2 et non decathlon ce qui explique les quelques différences de résultats que vous pouvez remarquer).
Pour ma part je suis totalement conquise par le package explor de Julien Barnier pour explorer mes résultats d’ACP (plus d’infos ici).
Ce package produit une interface Shiny qui vous permet de visualiser vos résultats et paramétrer finement vos sorties graphiques, décaler les étiquettes qui se chevaucheraient, etc. Et vous pouvez suite à ces manipulations soit exporter les figures (au format et dimensions de votre choix), soit copier le code R qui permet de produire les graphiques en question (dans un souci de reproductibilité de vos analyses…).
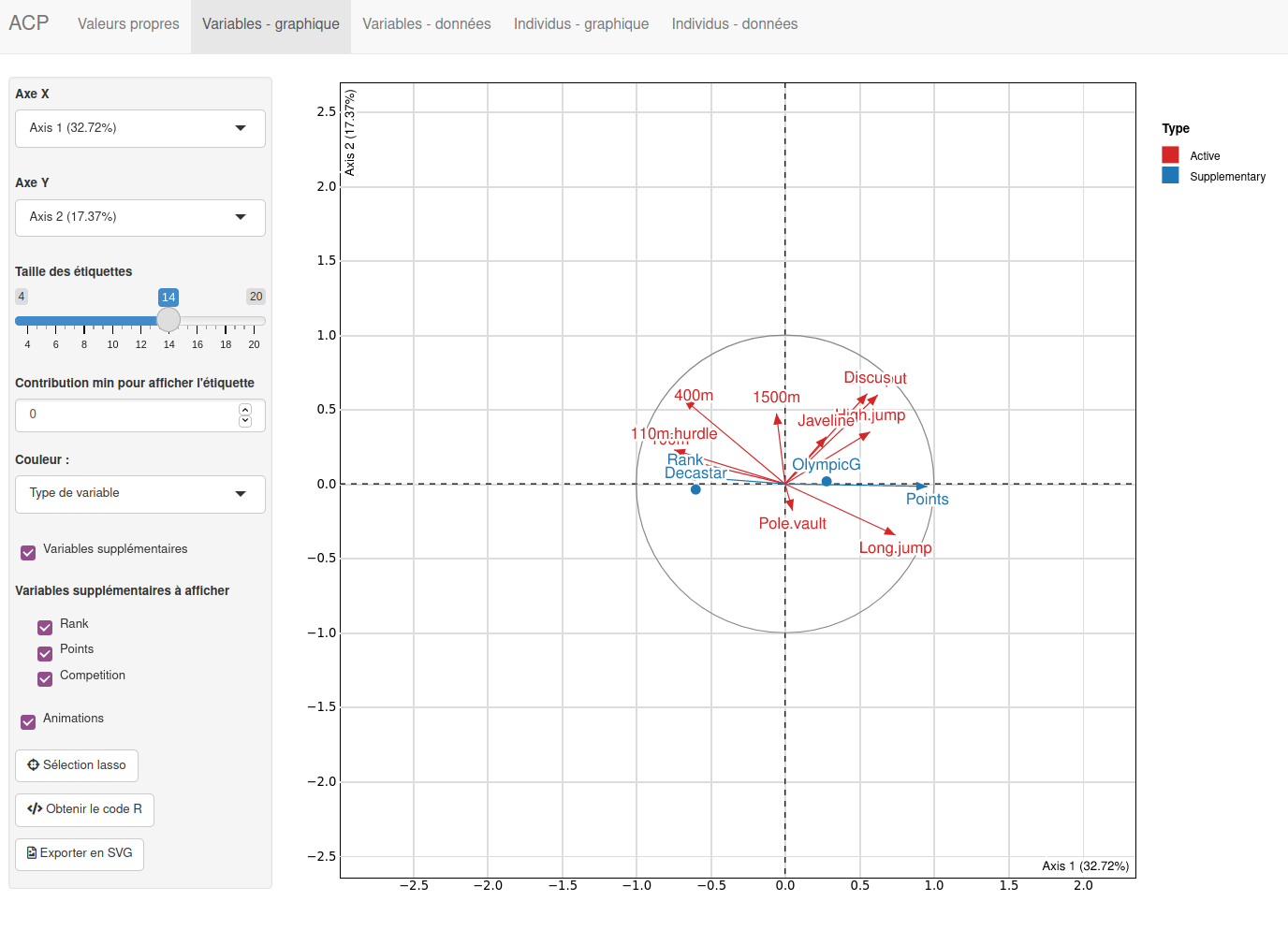
Pour lancer cette interface, c’est très simple. On réalise l’ACP avec le package de son choix (FactoMineR OU ade4!) et on lance la fonction explor() avec ce résultat d’ACP en objet:
resultat=PCA(decathlon, quanti.sup=11:12,quali.sup=13, graph=FALSE)
explor::explor(resultat)
Ici j’ai précisé que mon jeu de données comprenait des variables supplémentaires (que je désigne par le numéro de colonne) de manière à pouvoir les utiliser dans les sorties graphiques.
Petit “tweak” d’utilisation de ce package: Il m’arrive également, quand je souhaite faire des graphiques qui sortent un peu des sentiers battus avec des résultats issus d’analyses factorielles, de récupérer les résultats mis en forme par la fonction prepare_results() de ce package. Ensuite j’utilise les tableaux en sortie avec le combo magique tidyr-dplyr-ggplot2 et hop, je suis à même d’obtenir exactement le graphique que j’ai en tête…
3 Comments
Sam
Pensez-vous que le nombre de points représente bien la qualité d’un athlète.?
cherief
Merci beaucoup , vous m'avez sauvez dans cet examen
Maylis
Incroyable ! très clair, merci!!! Il nous faut plus de gens comme vous !