
Aïe aïe aïe!! Quelle prise de tête que les transformées d’ondelettes quand on n’est pas très matheux… Comprendre de A à Z comment elles fonctionnent, en déroulant tout le raisonnement de la définition d’une ondelette à l’interprétation finale de la transformée, c’est long, c’est compliqué, c’est même parfois impossible si on ne peut pas se lancer à corps perdu dans le sujet…
Ici, je pars du principe que vous non plus, vous n’êtes pas forcément prêts à faire le grand saut… alors je vais vous présenter une méthode liée aux transformées d’ondelettes discrètes, dite Analyse Multi-Résolution (MRA en anglais) en me concentrant sur le résultat plutôt que sur la méthode. J’ai tout un tas de supports éparpillés sur la méthode en question donc il n’est pas exclu que je me fende un jour d’un bon gros billet avec tout plein d’équations sur le sujet mais je ne voudrais pas vous faire peur d’emblée :-)…
Notez que dans cette même démarche (de démocratisation des ondelettes) j’ai également mis en ligne une appli permettant de tester tout un tas de méthodes d’analyse du signal par les ondelettes (ondelettes discrètes ou continues).
Les ondelettes discrètes, pour quoi faire?
Les transformées d’ondelettes peuvent servir à débruiter, filtrer, compresser, décomposer le signal et/ou sa variance en dissociant ses composantes à diverses échelles.
Pour ma part, je ne m’intéresse pas ces transformées pour la compression du signal mais plutôt à leur usage pour l’analyse de séries. Par ailleurs, je vais ici me concentrer sur l’analyse de séries (temporelles ou spatiales) 1D, excluant de ce fait l’analyse d’images (2D) de mon propos.
J’aimerais commencer en montrant rapidement ce que l’on peut réaliser à travers les transformées d’ondelettes. Considérons le signal suivant, qui correspond à une série de températures relevées à la station météo de Lyon Saint-Exupéry (température moyenne journalière, données disponibles sur ce site et que je vous remets ici. On devine dans ce signal une forte composante saisonnière (échelle temporelle “moyenne”), à laquelle se rajoute du “bruit” (échelle temporelle fine), et, peut-être, une tendance de fond (échelle temporelle longue) à l’augmentation de la température moyenne (on verra si nos analyses le confirment!). De fait, j’ai choisi ces données car elles se prêtent tout naturellement à une analyse multi-résolution!!
library(tidyverse)
data_ex=read.delim(paste0(dat.path,"TG_STAID000037.txt"),
sep=",", skip=20, na=-9999)%>%
mutate(x=lubridate::ymd(DATE),
y=TG/10) %>%
group_by(x) %>%
summarise(y=mean(y)) %>%
na.omit()
ggplot(data_ex,aes(x=x,y=y))+
geom_line(col="dark grey")
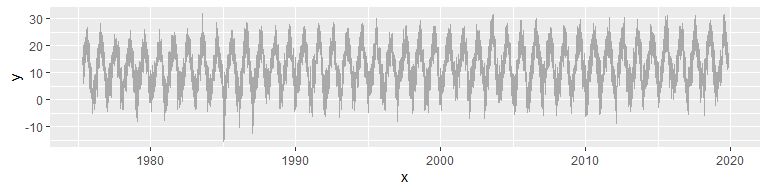
La décomposition en ondelettes discrètes permet de réaliser une analyse multi-résolution (MRA) du signal. Je passe pour l’instant sur le code qui permet de réaliser les graphiques suivants… mais j’y reviendrai! C’est à dire que l’on va pouvoir décomposer le signal en différentes composantes, qui correspondent à des échelles plus ou moins fines, et que cette décomposition aura l’intérêt d’être additive.
Si l’on considère la façon dont le signal est décomposé, étape par étape, on peut écrire les équations suivantes:
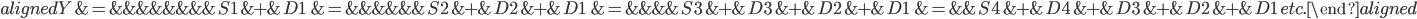
- D’abord, Y est décomposé à très petite échelle en un signal de “détail” (D1) et un signal lissé -“smooth”- (S1).
- Puis ce signal lissé à très petite échelle peut être lissé à une échelle un peu moins petite en un nouveau “smooth” (S2) et un nouveau “detail” (D2): S1 = S2 + D2.
- A nouveau, on peut lisser ce smooth une échelle un peu plus grande pour produire un nouveau smooth (S3) et un nouveau détail (D3): S2 = D3 + S3
- etc.
A la fin, on arrive toujours à une somme de sous-signaux égale au signal de départ, chaque sous-signal nous informant sur la variation à une échelle donnée, de manière non redondante par rapport aux autres sous-signaux.
Voyez à quoi la “pyramide” d’équations ci-dessus correspond en terme de représentation des variations du signal (j’ai représenté les séries verticalement pour une meilleure lisibilité):
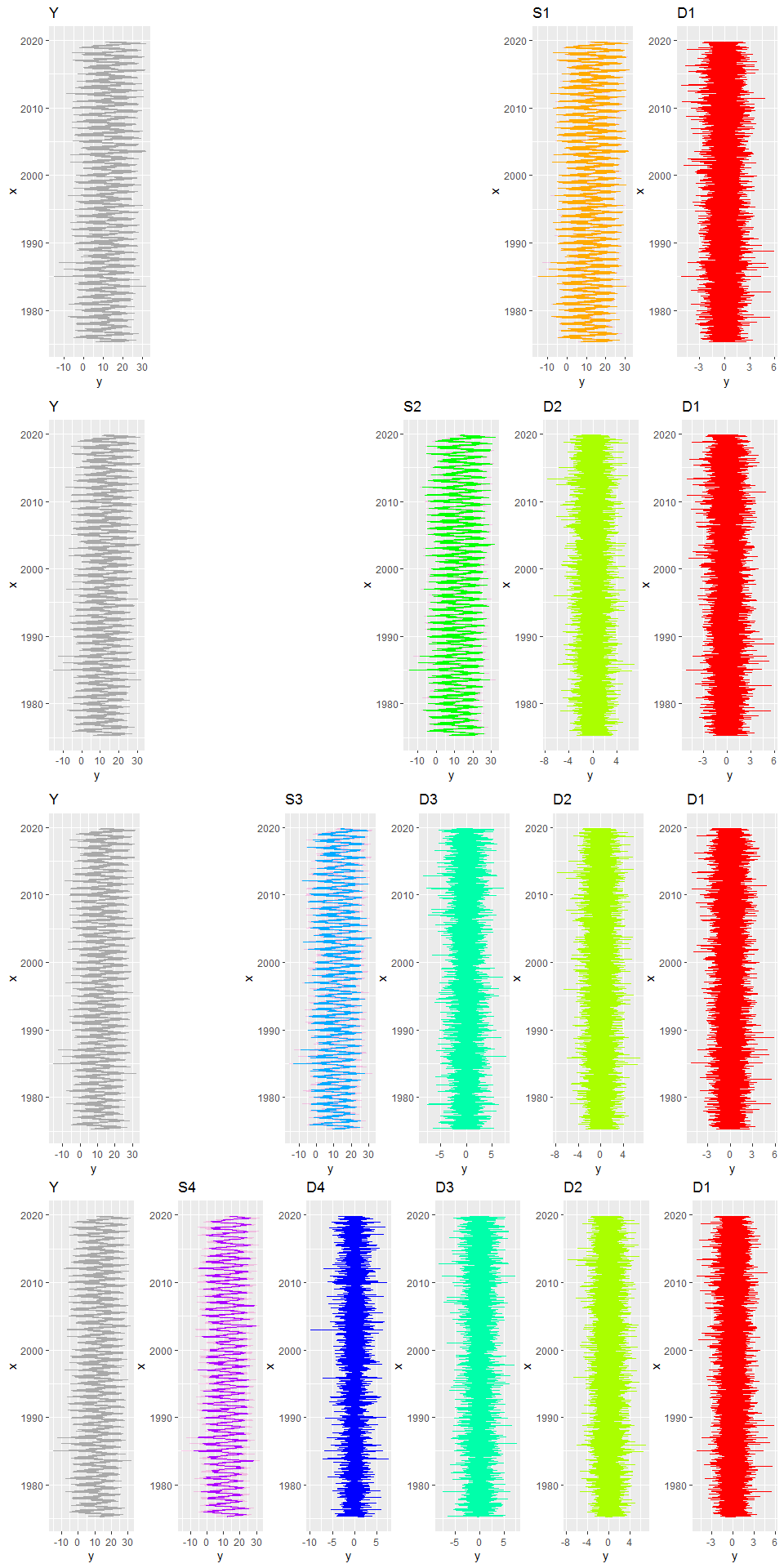
Il est en fait possible de lisser encore et encore ce signal, jusqu’à arriver à un smooth qui nous montre la tendance de fond. Ci-dessus je me suis arrêtée au niveau 4 car d’un point de vue graphique 4 niveaux de décomposition étaient déjà assez lourds…
Cela étant, rien ne nous empêche de regrouper certains sous-signaux… Par exemple, on peut essayer de distinguer une composante plutôt saisonnière (S4) au sein des variations journalières:
Y = S4 + (D4 + D3 + D2 + D1) 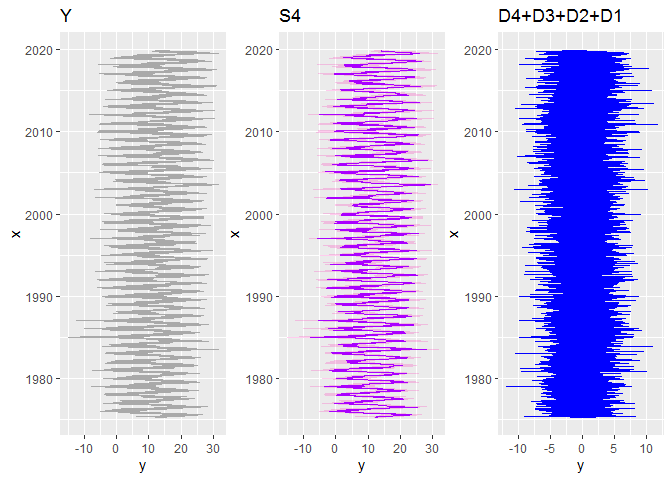
Ainsi, en poussant la décomposition plus loin, et en regroupant un certain nombre de niveaux, on peut essayer d’isoler une tendance de fond:
Y = S10 + (D10 + ... + D5) + (D4 + ... + D1) 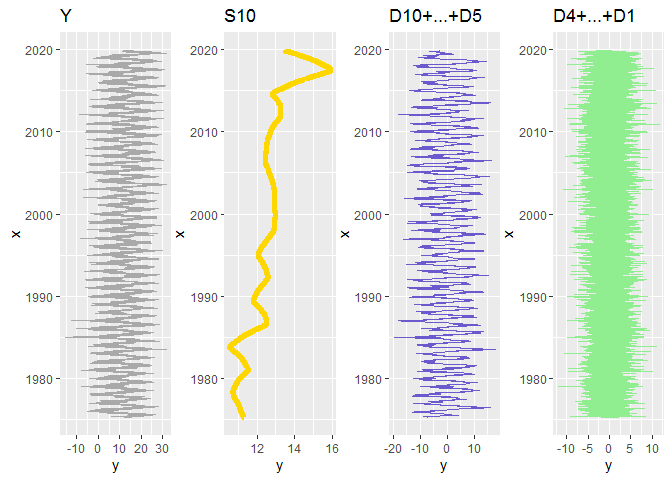
Bingo! L’examen des graphiques ci-dessus révèle par exemple:
- qu’il y a bien une tendance à l’augmentation de la température depuis 1975 (on ne nous aurait donc pas menti! :-p).
- il y a eu quelques années particulièrement froides dans la deuxième moitié des années 80 (on le voit sur S10) et en particulier un hiver 85 particulièrement rigoureux (on le voit sur D10+….+D5)
- on remarque les épisodes de canicule dans leur effet sur la composante saisonnière (D10+…+D4): voyez par exemple la canicule 2003 marquée par un pic plus marqué que les autres…
Comment faire, sous R?
Pour réaliser les transformées d’ondelettes discrètes sous R j’utilise un package qui s’appelle wavelets. Comme à mon habitude, je vais aussi utiliser le tidyverse pour réaliser les quelques traitements supplémentaires dont j’aurai besoin (et patchwork pour organiser mes panneaux de graphiques!)
library(wavelets)
library(tidyverse)
library(patchwork)
Voilà comment je réalise mon analyse multi-résolution, à l’aide de la fonction mra() du package wavelets:
mymra=mra(X=data_ex$y,
n.levels=10,
boundary="reflection")
- Le premier argument
Xcorrespond au signal lui-même. Pour que la transformée d’ondelettes ait un sens, il faut que la série de données corresponde à des valeurs Y régulièrement espacées (ici dans le temps). - Le deuxième argument
n.levelscorrespond au niveau maximal de décomposition (ce niveau maximal dépendra de la nature de l’ondelette et de la longueur de la série). - Le dernier argument
boundarycorrespond à la méthode utilisée “au bord du signal” pour calculer les transformées d’ondelettes. En effet, pour calculer les coefficients d’ondelettes sur les bords du signal, on est obligés d’allonger artificiellement le signal. Les deux choix possibles sont “periodic” (on recycle le signal, du début à la fin) ou “reflection” (on retourne le signal, en miroir). Dans notre cas de séries de températures, l’existence d’une évolution entre le début et la fin du signal (augmentation graduelle de la température moyenne) rend la transformation “reflection” plus pertinente…
Examinons maintenant ce que nous retourne la fonction mra():
str(mymra)
## Formal class 'mra' [package "wavelets"] with 9 slots
## ..@ D :List of 10
## .. ..$ D1 : num [1:32532, 1] 0.418 -1.058 0.292 0.332 -0.51 ...
## .. ..$ D2 : num [1:32532, 1] -0.538 -0.396 -0.244 0.316 1.119 ...
## .. ..$ D3 : num [1:32528, 1] 0.1031 -0.207 -0.5185 -0.3569 -0.0928 ...
## .. ..$ D4 : num [1:32528, 1] 2.249 2 1.697 1.147 0.477 ...
## .. ..$ D5 : num [1:32512, 1] 0.868 0.899 0.913 0.835 0.716 ...
## .. ..$ D6 : num [1:32512, 1] 0.861 1.047 1.215 1.3 1.343 ...
## .. ..$ D7 : num [1:32512, 1] -3.88 -3.89 -3.89 -3.84 -3.76 ...
## .. ..$ D8 : num [1:32512, 1] -2.47 -2.6 -2.72 -2.8 -2.87 ...
## .. ..$ D9 : num [1:32256, 1] -2.88 -2.94 -2.99 -3.02 -3.05 ...
## .. ..$ D10: num [1:31744, 1] 0.62 0.622 0.624 0.625 0.626 ...
## ..@ S :List of 10
## .. ..$ S1 : num [1:32532, 1] 13.8 14.3 14.7 15.2 15.7 ...
## .. ..$ S2 : num [1:32532, 1] 14.3 14.7 15 14.9 14.6 ...
## .. ..$ S3 : num [1:32528, 1] 14.5 14.4 14.2 13.8 13.2 ...
## .. ..$ S4 : num [1:32528, 1] 12.2 12.4 12.5 12.6 12.7 ...
## .. ..$ S5 : num [1:32512, 1] 12.9 13 13.1 13.2 13.3 ...
## .. ..$ S6 : num [1:32512, 1] 12 12 11.9 11.9 11.9 ...
## .. ..$ S7 : num [1:32512, 1] 15.9 15.8 15.8 15.7 15.7 ...
## .. ..$ S8 : num [1:32512, 1] 18.4 18.4 18.5 18.5 18.6 ...
## .. ..$ S9 : num [1:32256, 1] 11.5 11.5 11.5 11.5 11.5 ...
## .. ..$ S10: num [1:31744, 1] 11.3 11.3 11.3 11.3 11.3 ...
## ..@ filter :Formal class 'wt.filter' [package "wavelets"] with 7 slots
## .. .. ..@ L : int 8
## .. .. ..@ level : int 1
## .. .. ..@ h : num [1:8] 0.0322 0.0126 -0.0992 -0.2979 0.8037 ...
## .. .. ..@ g : num [1:8] -0.0758 -0.0296 0.4976 0.8037 0.2979 ...
## .. .. ..@ wt.class : chr "Least Asymmetric"
## .. .. ..@ wt.name : chr "la8"
## .. .. ..@ transform: chr "dwt"
## ..@ level : int 10
## ..@ boundary: chr "reflection"
## ..@ series : num [1:32532, 1] 14.2 13.2 15 15.5 15.2 14.4 12.3 11.7 15.2 16.4 ...
## ..@ class.X : chr "numeric"
## ..@ attr.X : list()
## ..@ method : chr "dwt"
Cet objet comprend un slot “filter” qui nous renseigne sur la nature de l’ondelette utilisée (car il existe plusieurs ondelettes possibles)! Ici, comme nous n’avons rien précisé dans l’appel à la fonction mra(), c’est par défaut l’ondelette “Least Asymetric” de longueur 8 (“la8”) qui a été utilisée (mais bien sûr nous aurions pu explicitement demander qu’une autre ondelette soit utilisée en utilisant l’argument filter):
mymra@filter
## An object of class "wt.filter"
## Slot "L":
## [1] 8
##
## Slot "level":
## [1] 1
##
## Slot "h":
## [1] 0.03222310 0.01260397 -0.09921954 -0.29785780 0.80373875 -0.49761867 -0.02963553 0.07576571
##
## Slot "g":
## [1] -0.07576571 -0.02963553 0.49761867 0.80373875 0.29785780 -0.09921954 -0.01260397 0.03222310
##
## Slot "wt.class":
## [1] "Least Asymmetric"
##
## Slot "wt.name":
## [1] "la8"
##
## Slot "transform":
## [1] "dwt"
Outre des informations sur la méthode de calcul et la nature de l’ondelette (slot “filter”), l’objet mymra comprend l’ensemble des smooths et des details pour les 10 niveaux de décomposition demandés ici. On peut accéder à chacun de ces sous-signaux de la manière suivante:
mymra@D$D1[1:5]
## [1] 0.4177861 -1.0581337 0.2924646 0.3321684 -0.5095316
Cela étant, quand on travaille dans la logique “tidy”, on a très envie d’obtenir tous ces sous-signaux comme autant de colonnes d’une table. Pour faciliter cette transformation, j’ai écrit une petite fonction add_wav_data():
add_wav_data=function(mydata,mra_obj){
n=nrow(mydata)
cut_to_size=function(x,n){
if(dim(x)[1]>n){
x=x[1:n]
}else{
x=c(x,rep(NA,n-dim(x)[1]))
}
return(x)
}
if(class(mra_obj)=="mra"){
S=mra_obj@S %>%
purrr::map(cut_to_size,n) %>%
bind_cols() %>%
mutate_all(as.vector)
D=mra_obj@D %>%
purrr::map(cut_to_size,n) %>%
bind_cols() %>%
mutate_all(as.vector)
wav_data=bind_cols(S,D)
}
mydata=bind_cols(mydata,
wav_data)
return(mydata)
}
data_ex_wav=add_wav_data(data_ex,mymra)
str(data_ex_wav)
## Classes 'tbl_df', 'tbl' and 'data.frame': 16266 obs. of 22 variables:
## $ x : Date, format: "1975-04-20" "1975-04-21" "1975-04-22" "1975-04-23" ...
## $ y : num 14.2 13.2 15 15.5 15.2 14.4 12.3 11.7 15.2 16.4 ...
## $ S1 : num 13.8 14.3 14.7 15.2 15.7 ...
## $ S2 : num 14.3 14.7 15 14.9 14.6 ...
## $ S3 : num 14.5 14.4 14.2 13.8 13.2 ...
## $ S4 : num 12.2 12.4 12.5 12.6 12.7 ...
## $ S5 : num 12.9 13 13.1 13.2 13.3 ...
## $ S6 : num 12 12 11.9 11.9 11.9 ...
## $ S7 : num 15.9 15.8 15.8 15.7 15.7 ...
## $ S8 : num 18.4 18.4 18.5 18.5 18.6 ...
## $ S9 : num 11.5 11.5 11.5 11.5 11.5 ...
## $ S10: num 11.3 11.3 11.3 11.3 11.3 ...
## $ D1 : num 0.418 -1.058 0.292 0.332 -0.51 ...
## $ D2 : num -0.538 -0.396 -0.244 0.316 1.119 ...
## $ D3 : num 0.1031 -0.207 -0.5185 -0.3569 -0.0928 ...
## $ D4 : num 2.249 2 1.697 1.147 0.477 ...
## $ D5 : num 0.868 0.899 0.913 0.835 0.716 ...
## $ D6 : num 0.861 1.047 1.215 1.3 1.343 ...
## $ D7 : num -3.88 -3.89 -3.89 -3.84 -3.76 ...
## $ D8 : num -2.47 -2.6 -2.72 -2.8 -2.87 ...
## $ D9 : num -2.88 -2.94 -2.99 -3.02 -3.05 ...
## $ D10: num 0.62 0.622 0.624 0.625 0.626 ...
## - attr(*, "na.action")= 'omit' Named int 1 2 3 4 5 6 7 8 9 10 ...
## ..- attr(*, "names")= chr "1" "2" "3" "4" ...
On est dès lors en mesure de faire notre petite tambouille (avec ggplot2, avec dplyr, etc.). Tenez, vérifions en deux coups de cuillère à pot que la décomposition du signal est bien additive:
data_ex_wav %>%
mutate(somme=S10+D10+D9+D8+D7+D6+D5+D4+D3+D2+D1) %>%
select(y,somme) %>%
head(n=10)
## # A tibble: 10 x 2
## y somme
## <dbl> <dbl>
## 1 14.2 6.66
## 2 13.2 4.79
## 3 15 5.69
## 4 15.5 5.84
## 5 15.2 5.30
## 6 14.4 4.72
## 7 12.3 2.84
## 8 11.7 1.28
## 9 15.2 3.70
## 10 16.4 2.96
En outre, je peux utiliser ce tableau à ma guise pour réaliser un graphique montrant les composantes de mon choix:
pbase=ggplot(data_ex_wav,aes(x=x,y=y))
pY =pbase+
geom_line(col="dark grey")+ggtitle("Y")
pDall=pbase +
geom_line(aes(x=x,y=D4+D3+D2+D1),col="lightgreen")+
ggtitle("D4+...+D1")
pDseason=pbase+
geom_line(aes(x=x,y=D10+D9+D8+D7+D6+D5), col="slateblue")+
ggtitle("D10+...+D5")
pTrend=pbase+
geom_line(aes(x=x,y=S10),col="gold",size=2)+
ggtitle("S10")
pY/pTrend/pDseason/pDall
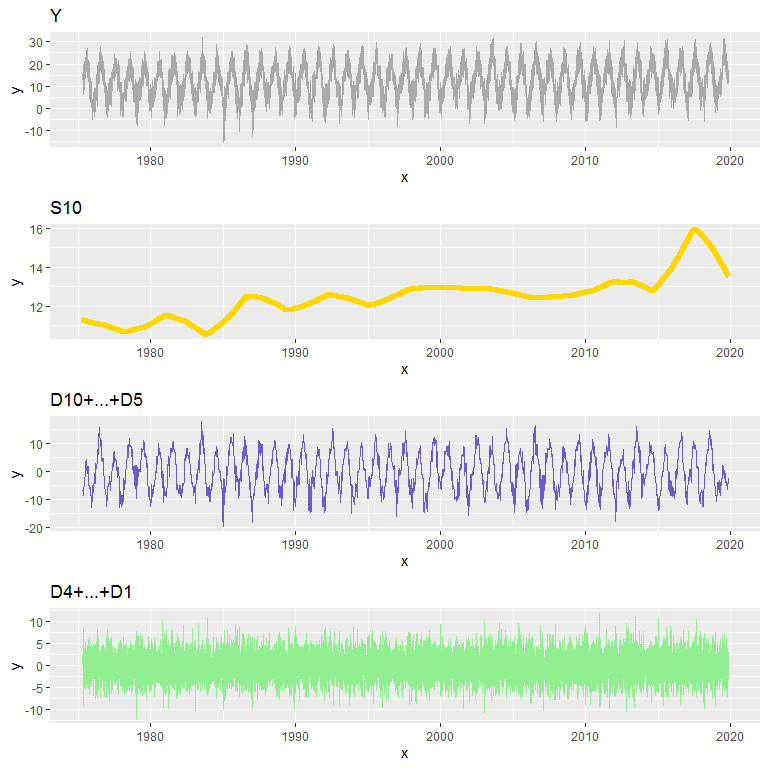
1 Comment
Alex
Merci pour ce petit tuto qui m'a permis de replonger dans le bain de l'analyse multi-résolution sans me noyer !