plot of chunk Lise_Vaudor_headband

Si vous travaillez sur des séries (temporelles, ou spatiales) alors ce qui suit pourrait vous intéresser.

Comment faire, en effet, pour décrire et analyser des séries telles que celles-ci:

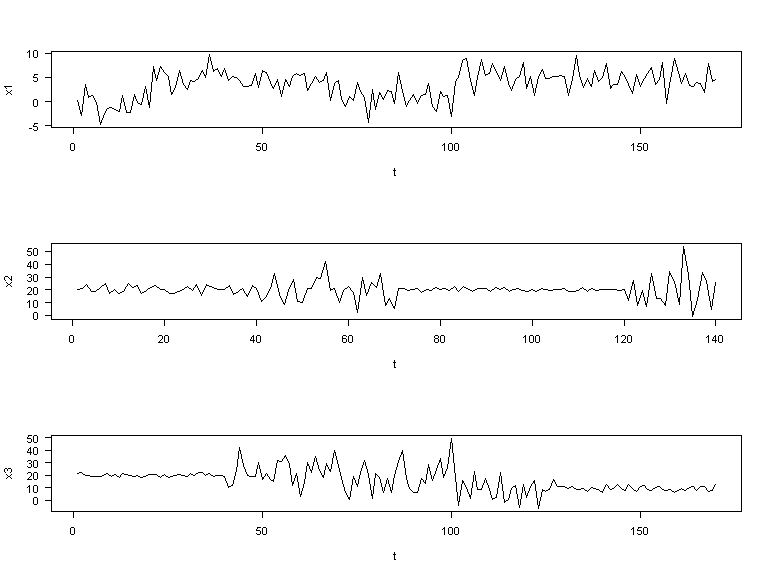
plot of chunk series

Il y a évidemment des manières très différentes de procéder pour analyser ce type de signal. L'une des plus "intuitives" consiste à découper la série en segments "homogènes". Cette notion d'homogénéité peut recouvrir, par exemple, une homogénéité en moyenne, ou une homogénéité en variance (ou encore une homogénéité en moyenne-variance!).

Exemple: détection de ruptures de moyenne, de variance, et de moyenne ou variance

Par exemple, pour les trois séries ci-dessus, on a l'impression que:

  • la série x1 est affectée par des changements de moyenne,
  • la série x2 est affectée par des changements de variance, et
  • la série x3 par des changements de moyenne et de variance.

Partant de ces modèles voici le genre de segmentation que l'on pourrait proposer:

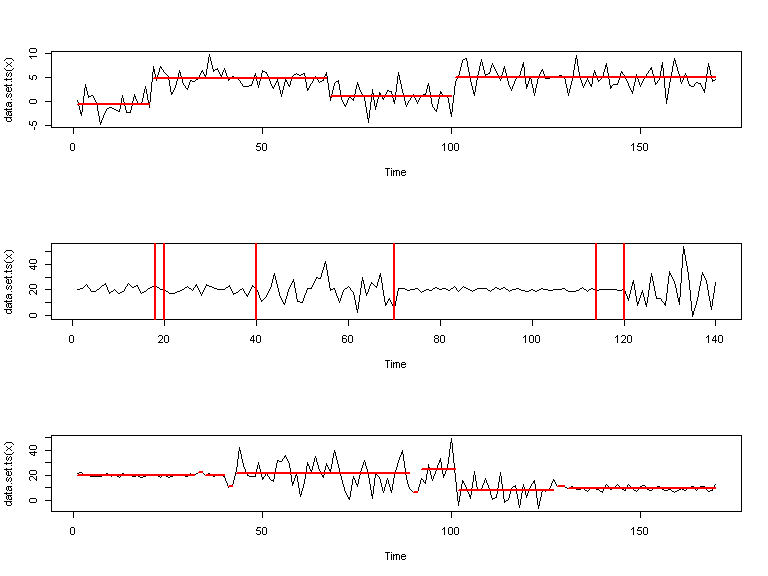
plot of chunk series_segmentees

Package changepoint

Les résultats ci-dessus sont en fait obtenus en utilisant le package changepoint de Killick and Eckley (2011).

En l'occurrence, voici les codes utilisés pour générer les segmentations ci-dessus:

layout(matrix(1:3,nrow=3))
require(changepoint)

###
seg1=cpt.mean(x1,method="PELT", penalty="Manual", pen.value="5*log(n)")
plot(seg1,cpt.width=2)
###
seg2=cpt.var(x2,method="PELT")
plot(seg2,cpt.width=2)
###
seg3=cpt.meanvar(x3,method="PELT")
plot(seg3,cpt.width=2)

On a utilisé 3 fonctions différentes:

  • cpt.mean qu'on utilise pour détecter des ruptures dans la moyenne (sous hypothèse que la variance est constante)
  • cpt.var qu'on utilise pour détecter des ruptures dans la variance (sous hypothèse que la moyenne est constante)
  • cpt.meanvar qu'on utilise pour détecter des ruptures à la fois dans la moyenne et dans la variance

Ces trois fonctions sont largement paramétrables. On peut ainsi faire varier (entre autres)

  • la nature de l'algorithme utilisé pour détecter les points de rupture "optimaux"
  • le type de test utilisé pour localiser les ruptures (on peut soit supposer que la distribution résiduelle des variables est gaussienne, soit ne pas faire d'hypothèse de distribution et utiliser un test non-paramétrique)
  • le type et l'ampleur de la pénalisation appliquée afin de limiter la sursegmentation.

Ces aspects sont discutés dans l'article de Killick and Eckley (2014)

Effet de la paramétrisation

Sans surprise, les fonctions ci-dessus donnent des résultats très différents selon la façon dont on les paramètre...

Par exemple ici, on fait varier le type d'algorithme:

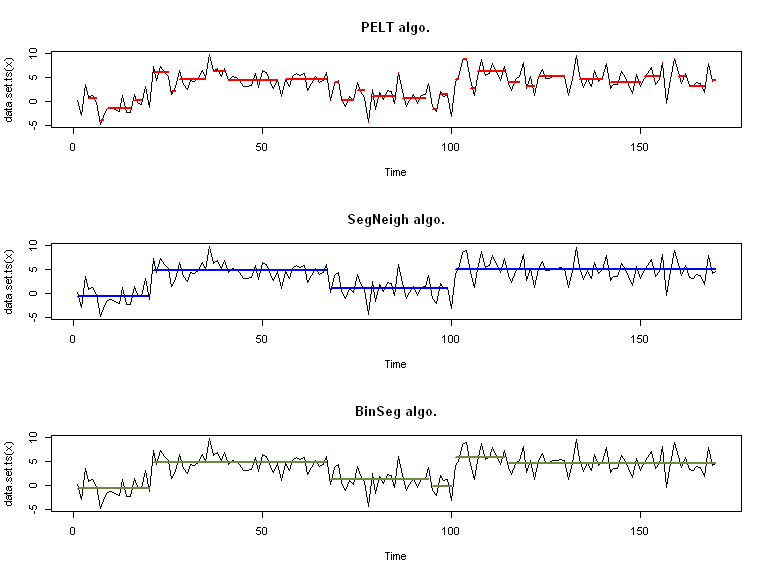
plot of chunk series_segmentees_param1

Ici, on fait varier le type de pénalité:

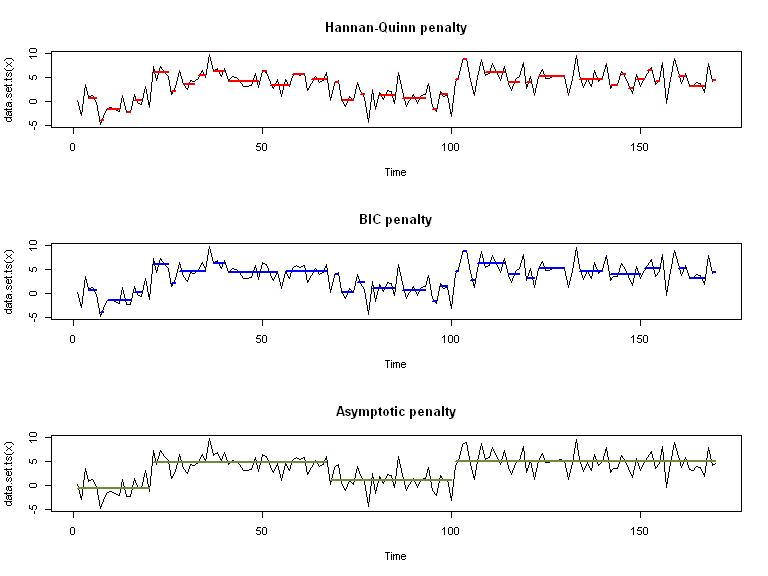
plot of chunk series_segmentees_param2

Et ici, on fait varier la valeur de la pénalité (quand fixée manuellement):

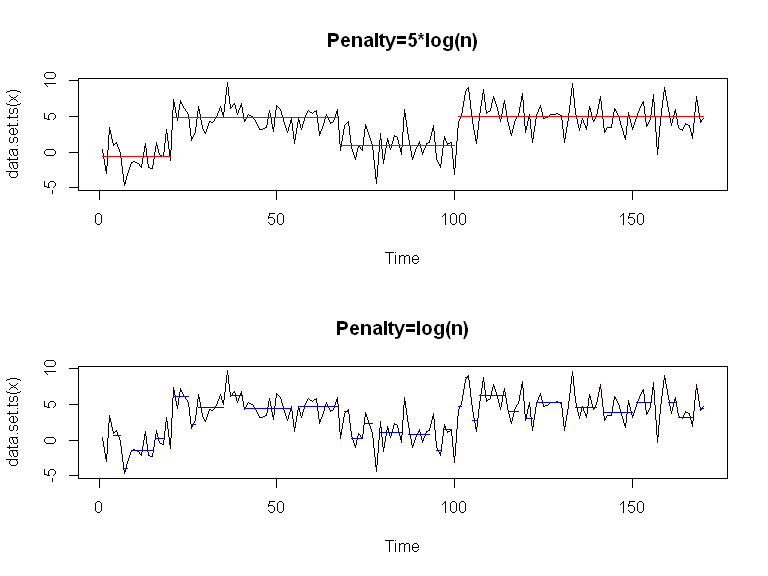
plot of chunk series_segmentees_param3

Comment choisir une méthode?

Pour choisir l'algorithme de segmentation et autres paramètres associés, on va s'appuyer sur 3 critères:

  • des critères théoriques (quel modèle est le plus adapté à vos données? un avec une variance constante, un où les résidus sont gaussiens, un qui rendrait compte de segments de longueurs très variables? etc.)
  • des critères empiriques (on choisit la méthode qui donne les résultats les plus "exploitables" sur des données réelles, et les plus corrects sur des données simulées)
  • des critères de calcul (il faut que pour des données d'une certaine taille, la méthode soit applicable d'un point de vue calculatoire)

Evidemment, déterminer quelle est la meilleure méthode en utilisant de multiples critères de ces trois types est difficile (voire impossible). Néanmoins il est possible d'en discuter en réalisant (peut-être, tout-de-même, en moins ambitieux!!) le même type d'étude que Leviandier et al. (2012).

Ce n'est pas l'objet de ce billet (ce serait un petit peu long), mais je compte me pencher sur cette question dans les mois qui viennent... Je n'exclus donc pas de futurs billets sur ce problème (ou assimilés)...

Réferences

Killick, Rebecca, and Idris A. Eckley. 2011. changepoint: An R Package for Changepoint Analysis. http://CRAN.R-project.org/package=changepoint.

———. 2014. “changepoint: An R Package for Changepoint Analysis.” Journal of Statistical Software 58 (3). http://www.jstatsoft.org/v58/i03.

Leviandier, Thierry, A. Alber, F. Le Ber, and H. Piégay. 2012. “Comparison of Statistical Algorithms for Detecting Homogeneous River Reaches Along a Longitudinal Continuum.” Geomorphology 138 (1): 130–44. doi:10.1016/j.geomorph.2011.08.031. http://linkinghub.elsevier.com/retrieve/pii/S0169555X11004624.