Pour analyser une variable binaire (dont les valeurs seraient VRAI/FAUX, 0/1, ou encore OUI/NON) en fonction d'une variable explicative quantitative, on peut utiliser une régression logistique.

Considérons par exemple les données suivantes, où x est l'âge de 40 personnes, et y la variable indiquant s'ils ont acheté un album de death metal au cours des 5 dernières années (1 si "oui", 0 si "non")

Graphiquement, on constate que vraisemblablement, plus les personnes sont âgées, moins elle achètent de death metal.

plot(x,y)

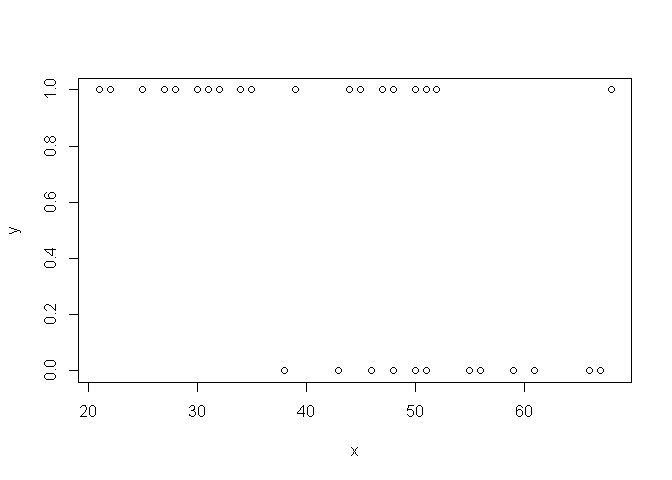
Vérifions cela à l'aide d'un modèle...

La régression logistique est un cas particulier de Modèle Linéaire Généralisé (GLM).

Avec un modèle de régression linéaire classique, on considère le modèle suivant:

     Y=\alpha X+\beta

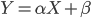
On prédit donc l'espérance de Y de la manière suivante :

     E(Y)=\alpha E(X)+ \beta

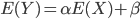
Ici, du fait de la distribution binaire de Y, les relations ci-dessus ne peuvent pas s'appliquer. Pour "généraliser" le modèle linéaire, on considère donc que

     g(E(Y)) =\alpha E(X)+ \beta

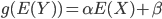
où g est une fonction de lien.

En l'occurence, pour une régression logistique, la fonction de lien correspond à la fonction logit:

     logit(p)=log(\frac{p}{1-p})

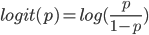
Notez que cette fonction logit transforme une valeur (p) comprise entre 0 et 1 (comme une probabilité par exemple) en une valeur comprise entre  − ∞ et  + ∞.

Voici comment réaliser la régression logistique sous R:

myreg=glm(y~x, family=binomial(link=logit))
summary(myreg)

## 
## Call:
## glm(formula = y ~ x, family = binomial(link = logit))
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.8686  -0.7764   0.3801   0.8814   2.0253  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)   
## (Intercept)   5.9462     1.9599   3.034  0.00241 **
## x            -0.1156     0.0397  -2.912  0.00360 **
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 52.925  on 39  degrees of freedom
## Residual deviance: 39.617  on 38  degrees of freedom
## AIC: 43.617
## 
## Number of Fisher Scoring iterations: 5

On obtient donc le modèle suivant:

     logit(E(Y))=-0.12 X + 5.95

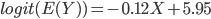
et l'on constate que l'influence (négative) de l'âge sur l'achat d'albums de death metal est bien significative au seuil de 5%.

Si l'on représente cette relation entre logit(E(Y) et X, on retrouve bien une relation linéaire. En revanche, l'échelle des ordonnées n'est pas aisée à interpréter... On procède donc à une transformation inverse de la relation:

logit_ypredit=-0.12*x+5.95
ypredit=exp(logit_ypredit)/(1+ exp(logit_ypredit)) # transfo inverse de logit

plot(x,y)
points(x,ypredit, col="red")

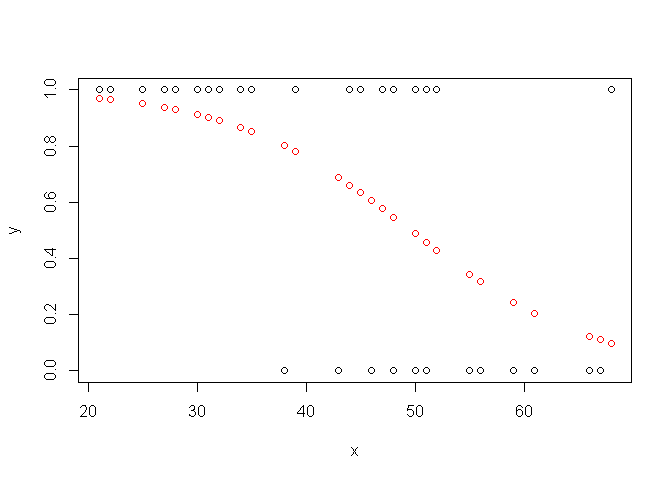
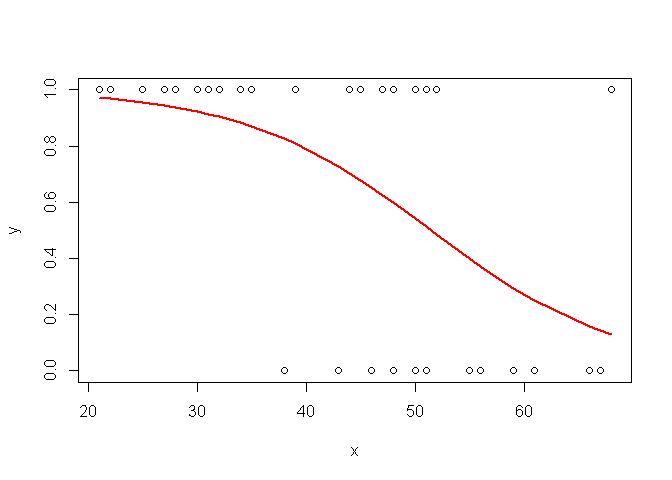
Pour tracer la courbe:

plot(x,y)
o=order(x)
points(x[o],ypredit[o], col="red", type="l", lwd=2)

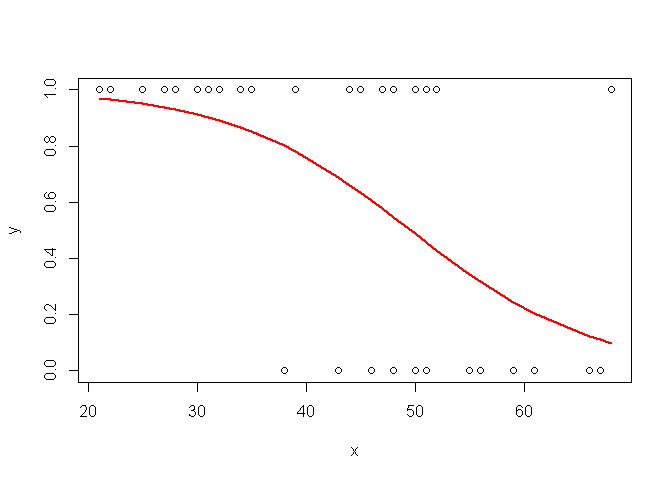
Enfin, pour se simplifier la vie, il est aussi possible de récupérer les valeurs prédites de y directement :

plot(x,y)
myreg=glm(y~x, family=binomial(link=logit))
ypredit=myreg$fitted
o=order(x)
points(x[o],ypredit[o], col="red", type="l", lwd=2)