
Mise à jour de ce billet: novembre 2020. => passage au
tidyverse pour la manipulation des tables de données et les graphiques.
A quoi sert-il?
Le test U de Mann-Whitney (aussi appelé test de la somme des rangs
de Wilcoxon ou plus simplement test de Wilcoxon) sert à tester
l’hypothèse selon laquelle la distribution des données est la même
pour deux groupes.
La p-value associée à ce test va ainsi répondre à la question
suivante:
Si les données pour les deux groupes étaient issues d’une même
population, quelle serait la probabilité que l’on observe par hasard
une différence de rangs(ou localisations) entre les deux groupes aussi
forte que celle observée sur les données?
Le test U de Mann-Whitney est souvent utilisé comme solution alternative
à l’utilisation d’un test de Student (t-test) dans le cas où les
données ne sont pas distribuées selon une loi normale et/ou dans le cas
où les données sont peu nombreuses. Il s’agit en effet d’un test
non-paramétrique, i.e. un test qui ne repose pas sur une hypothèse de
distribution des données.
Un exemple
Considérons les données suivantes:
library(tidyverse)
tib=tibble(x=c("A","A","A","A","A","A","A", "A" ,
"B","B","B","B","B","B"),
y=c(1.5,6.3,2.4,4.1,1.2,5.3,15.2,10.6,
2.5,3.3,1.3,2.1,5.7,1.1))
ggplot(tib, aes(x=x, y=y))+
geom_boxplot(aes(fill=x))+
scale_fill_manual(values=c("A"="pink",
"B"="lightsteelblue3"))
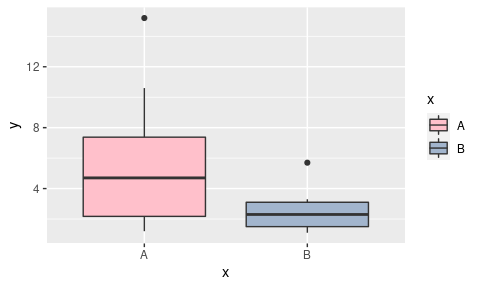
On a ici des données qui ne sont ni franchement nombreuses, ni
franchement normales.
Comment faire un test U de Mann-Whitney sous R?
montest=wilcox.test(y~x, data=tib)
montest
##
## Wilcoxon rank sum test
##
## data: y by x
## W = 34, p-value = 0.2284
## alternative hypothesis: true location shift is not equal to 0
Ici, la p-value est plus grande que 0.05: on ne parvient pas à rejeter
l’hypothèse selon laquelle les données des deux groupes proviennent
d’une même distribution au seuil α = 0.05.
Sur quelle métrique le test de Mann-Whitney se base-t-il?
Le test U de Mann-Whitney calcule une p-value qui se base non pas sur
les données brutes, mais sur leurs rangs. Les rangs en question
correspondent à l’emplacement de chaque donnée au sein de la série
lorque cette série est ordonnée par ordre croissant.
tib=tib %>%
mutate(rangs=rank(y))
tib
## # A tibble: 14 x 3
## x y rangs
## <chr> <dbl> <dbl>
## 1 A 1.5 4
## 2 A 6.3 12
## 3 A 2.4 6
## 4 A 4.1 9
## 5 A 1.2 2
## 6 A 5.3 10
## 7 A 15.2 14
## 8 A 10.6 13
## 9 B 2.5 7
## 10 B 3.3 8
## 11 B 1.3 3
## 12 B 2.1 5
## 13 B 5.7 11
## 14 B 1.1 1
Les distributions des rangs sont beaucoup moins affectées par
l’existence de valeurs extrêmes que ne le sont les distributions des
valeurs brutes:
ggplot(tib, aes(x=x, y=rangs))+
geom_boxplot(aes(fill=x))+
scale_fill_manual(values=c("A"="pink",
"B"="lightsteelblue3"))
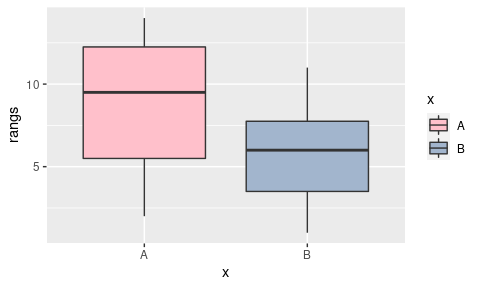
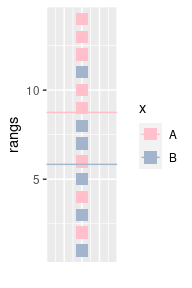
Représentons les rangs des individus ainsi que l’appartenance de ces
individus aux deux groupes. Les individus du groupe A sont représentés
en rose, les individus du groupe B en bleu. Les pointillés représentent
la moyenne des rangs pour chacun des groupes
tib_summary=tib %>%
group_by(x) %>%
summarise(loc=mean(rangs),
.groups="drop")
ggplot(tib %>% mutate(xx=0),
aes(x=xx,y=rangs))+
geom_point(aes(col=x), pch=15, size=4)+
geom_hline(data=tib_summary,
aes(yintercept=loc, col=x))+
scale_color_manual(values=c("A"="pink",
"B"="lightsteelblue3"))+
guides(x="none")+xlab("")
Le test de Mann-Whitney peut se baser sur une métrique W (en lien avec
la dénomination “test de Wilcoxon”) qui correspond à
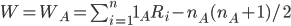
On peut aussi définir WB :
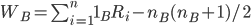
n correspond à l’effectif total, nA l’effectif du
groupe A, nB l’effectif du groupe B, et
Ri correspond au rang du i-ième individu.
Les nombres nA(nA + 1)/2 et
nB(nB + 1)/2 correspondent en fait à ce
que serait la somme des rangs si tous les individus du groupe A
(respectivement B) avaient les rangs 1,2,3,….,nA
(respectivement 1,2,3,…,nB).
W est ainsi d’autant plus grand que les individus du groupe A présente
des rangs élevés au sein de l’ensemble des individus.
Alternativement, on pourrait considérer la métrique U (en lien avec la
dénomination “test U de Mann-Whitney”) qui correspond à:
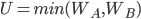
Cette métrique est quant à elle d’autant plus faible que l’un ou l’autre
des groupes présente des rangs bas.
Calculons la métrique W pour nos données:
tib_summary=tib %>%
group_by(x)%>%
summarise(n=n(),
loc=mean(rangs),
SR_0=n*(n+1)/2,
SR=sum(rangs),
W=SR-SR_0,
.groups="drop")
tib_summary
## # A tibble: 2 x 6
## x n loc SR_0 SR W
## <chr> <int> <dbl> <dbl> <dbl> <dbl>
## 1 A 8 8.75 36 70 34
## 2 B 6 5.83 21 35 14
On retrouve bien la valeur de W (34) qui était indiquée en sortie du
test de Mann-Whitney réalisé ci-dessus.
En l’occurence, par construction on a toujours
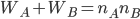
On peut le vérifier ici:
tib_summary %>%
summarise(sum(W),
prod(n),
.groups="drop")
## # A tibble: 1 x 2
## `sum(W)` `prod(n)`
## <dbl> <dbl>
## 1 48 48
A quoi la p-value correspond-elle?
Supposons que le groupe A ne corresponde pas à des rangs
particulièrement élevés dans la série. Dans ce cas, les rangs observés
pour A sont comme “attribués au hasard”. Quelle est alors la
distribution de W?
Pour répondre à cette question nous allons simuler un grand nombre
d’échantillons au hasard
- correspondant à des rangs entre 1 et
nA + nB = 14 - tels que nA = 8 des individus soient étiquetés comme
appartenant au groupe A - tels que nB = 6 des individus soient étiquetés comme
appartenant au groupe B
Nous calculerons pour chaque simulation la valeur de W.
niter=10000
vecteur_W=rep(NA,niter)
for (i in 1:niter){
tib_sim=tib %>%
# On réattribue au hasard les rangs aux données
# (i.e. aux différents groupes):
mutate(r_sim=sample(rangs,n(),replace=F)) %>%
group_by(x) %>%
# On calcule la statistique correspondant à
# la somme des rangs observés SR_i
summarise(n=n(),
SR_0=n*(n+1)/2,
SR_i=sum(r_sim),
.groups="drop") %>%
# On calcule la statistique W
mutate(Wsim=SR_i-SR_0)
# On récupère W_A pour l'itération,
# et on la stocke dans vecteur_W
vecteur_W[i]=tib_sim %>% filter(x=="A") %>% pull(Wsim)
}
hist(vecteur_W,freq=F,
col="lemonchiffon",
main="distrib. de W sous hypothèse nulle")
abline(v=tib_summary %>% filter(x=="A") %>% pull(W), lty=3,lwd=3, col="red")
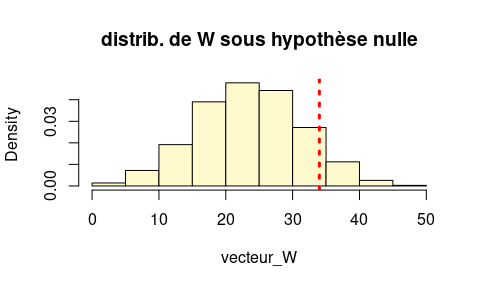
La distribution empirique de W nous permet de calculer la p-value
correspondant au test de l’hypothèse “A n’a pas une localisation
particulièrement élevée”.
wilcox.test(y~x,alternative="less", data=tib)
##
## Wilcoxon rank sum test
##
## data: y by x
## W = 34, p-value = 0.9094
## alternative hypothesis: true location shift is less than 0
print(length(which(vecteur_W>=montest$statistic))/niter)
## [1] 0.1167
Ici on veut en fait faire un test bilatéral : notre hypothèse nulle
“la distribution des données est la même pour les deux groupes”
correspond en fait à deux sous-hypothèses:
- “A n’a pas une localisation particulièrement élevée” ET
- “A n’a pas une localisation particulièrement basse” (i.e. “B n’a pas
une localisation particulièrement élevée”)
On s’interroge ainsi non seulement sur la distribution de
WA mais aussi sur la distribution de WB.
Or ces deux distributions sont en fait les mêmes… Vous pouvez le
vérifier comme suit:
layout(matrix(1:2,nrow=1))
vecteur_W_A=vecteur_W
vecteur_W_B=tib_summary %>% mutate(prodn=prod(n)) %>% pull(prodn)-vecteur_W_A
hist(vecteur_W_A,freq=F,
col="lemonchiffon",
main="distrib. de W_A")
hist(vecteur_W_B,freq=F,
col="lemonchiffon",
main="distrib. de W_B")
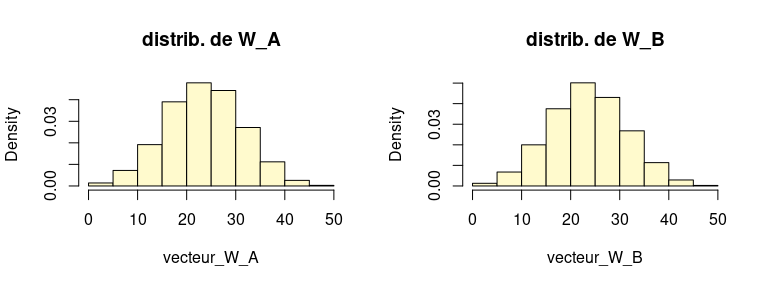
On peut ainsi retrouver la p-value fournie par le test:
print(2*length(which(vecteur_W>=montest$statistic))/niter)
## [1] 0.2334
print(montest$p.value)
## [1] 0.2284382
Comment R calcule-t-il la p-value?
Ci-dessus, j’ai montré comment on peut recalculer “à la main” la p-value
fournie par le test. En fait, pour des valeurs de nA et
nB assez élevées, la distribution de W est
approximativement normale (R n’a pas besoin d’effectuer des simulations,
comme nous l’avons fait, pour calculer la p-value).
Pour des valeurs de nA et nB relativement
faibles, les p-values sont tabulées (c’est-à-dire que pour des
valeurs nA et nB faibles, R a en mémoire
les quantiles de la distribution de W). Cependant, de la même manière
que dans nos simulations ci-dessus, ces p-values ont été calculées en
supposant qu’il n’y avait pas d’ex-aequos (i.e. pour calculer ces
quantiles, il a été supposé que les rangs étaient 1,2,3,….,n, et non,
par exemple, 2,2,2,3,4,5,…,n). C’est la raison pour laquelle R affiche
des Warnings dans le cas où
- les données sont peu nombreuses ET
- il y a des ex-aequos.
tib=tibble(x=c("A","A","A","A",
"B","B","B","B","B","B"),
y=c(1.5,6.3,6.3,2.7,
2.5,3.3,1.3,2.1,5.7,1.1))
wilcox.test(y~x, data=tib)
## Warning in wilcox.test.default(x = c(1.5, 6.3, 6.3, 2.7), y = c(2.5, 3.3, : cannot compute exact p-value with ties
##
## Wilcoxon rank sum test with continuity correction
##
## data: y by x
## W = 18, p-value = 0.2395
## alternative hypothesis: true location shift is not equal to 0
Pour des échantillons plus grands, on n’a pas ce même message d’erreur
car la p-value est calculée en se basant sur l’approximation normale:
tib=tibble(x=c(rep("A",50) , rep("B",50)),
y=c(rlnorm(50,3,2), rlnorm(50,4,2))) %>%
# repetition des 10 premieres valeurs => ex-aequos
mutate(y=c(y[11:20],y[11:100]))
wilcox.test(y~x, data=tib)
##
## Wilcoxon rank sum test with continuity correction
##
## data: y by x
## W = 1045, p-value = 0.1586
## alternative hypothesis: true location shift is not equal to 0
11 Comments
Carine
Bonjour,
J'aimerai savoir s'il est possible de prendre en compte la répétition. Par exemple, lorsque au sein d'un groupe il a été effectué plusieurs fois la mesure pour chaque individu.
Merci, Carine
karim bensaid
très belle démonstration! merci bcp . très utile
Difah
Merci beaucoup
Maïa
Bonjour,
Vous dites que la p-value associée au test répond à la question suivante : "Si les données pour les deux groupes étaient issues d'une même population, quelle serait la probabilité que l'on observe par hasard une différence de rangs (ou localisations) entre les deux groupes aussi forte que celle observée sur les données?" or la definition exacte de la p-value est en fait "Si les données pour les deux groupes étaient issues d'une même population, quelle serait la probabilité que l'on observe une différence de rangs (ou localisations) AU MOINS AUSSI EXTRÊME entre les deux groupes aussi forte que celle observée sur les données?"
Merci pour ce chouette blog !
lvaudor
Bonjour,
C'est vrai, mon "aussi forte" était ambigü... j'ai remplacé par "au moins aussi extrême", comme vous me l'avez suggéré!!
Merci!
Liping
Bonjour,
Je voudrais savoir comment il range les échantillons avec des valeurs avec 0? ça veut dire que s'il contribue aussi un range aux données avec une valeur à zéro?
Merci d'avance!
lvaudor
Bonjour,
Si l'échantillon contient des valeurs ex-aequos (zéros ou autres), ces valeurs sont bien prises en compte dans le calcul du W observé. Par contre, le test renvoie un warning stipulant que le calcul de la p-value peut être inexact du fait de ces ex-aequos. Je n'ai pas épluché le code donc je ne suis pas sûre de ce que j'avance, mais a priori je dirais qu'on attribue arbitrairement un rang différent à ces valeurs pour pouvoir calculer une statistique W observée, même si le calcul de la distribution théorique de W se fait en faisant l'hypothèse qu'il n'y a pas d'ex-aequos (d'où le warning).
Epitace
Merci beaucoup
Julie
Bonjour,
Merci pour ces explications !
Est-il possible d'avoir la commande R que vous avez utilisée pour tracer les rangs avec une couleur différente selon le groupe ?
Merci d'avance
lvaudor
Bonjour Julie,
Le billet était assez ancien et n'utilisait pas le tidyverse (ggplot2, dplyr) qui font désormais partie (à mon avis) des incontournables pour travailler sous R. J'ai donc "profité" de votre demande pour mettre à jour le billet en ce sens et faire apparaître l'ensemble des codes qui permettent de générer les figures.
Julie
Merci beaucoup !