Test des contrastes de Scheffé

plot of chunk
Lise_Vaudor_headband

Le test de Scheffé est un test qu'on applique souvent après une ANOVA: on parle de test post-hoc (au même titre, par exemple, qu'un test de Tukey). En effet, l'ANOVA à 1 facteur permet de mettre en évidence (le cas échéant) le fait qu'au moins un groupe a une moyenne différente des autres. Si on a affaire à 3 groupes ou plus, une question se pose alors: quels sont les groupes différents deux à deux?

Le test de Scheffé, en pratique:

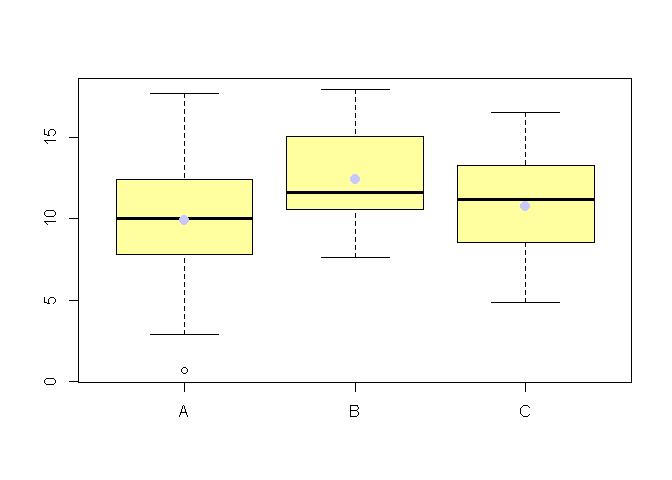
plot of chunk
exemple_donnees_ANOVA_3_niveaux

Testons la significativité de l'effet de X sur Y à travers une ANOVA:

mymod=lm(Y~X)
anova(mymod)

## Analysis of Variance Table
## 
## Response: Y
##           Df Sum Sq Mean Sq F value Pr(>F)  
## X          2     61    30.7    2.55  0.087 .
## Residuals 59    710    12.0                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

On rejette l'hypothèse d'égalité de toutes les moyennes au seuil de α = 10%.

Il n'existe pas à l'heure actuelle de test de Scheffé sous R.

_{^{(en fait, si, il y a une fonction scheffe.test dans un package qui s'appelle agricolae, mais il me semble après l'avoir testée qu'il y ait une petite erreur dans cette fonction, alors en attendant que son auteur la corrige -ça ne devrait pas être bien long- on va faire comme s'il n'y avait rien...).}}

Je vous propose d'utiliser une petite fonction que j'ai écrite (vous trouverez des explications sur le code dans le paragraphe suivant) et disponible ici.

Voici comment utiliser cette fonction:

source("test_Scheffe_maison.R")
Scheffe.test(X,Y,alpha=0.1)

##     contrast sigma    LCI    UCI    pval
## A-B   -2.555 1.133 -5.034 -0.076 0.08718
## A-C   -0.868 1.014 -3.087  1.352 0.69507
## B-C    1.688 1.161 -0.854  4.229 0.35448

Les résultats du test de Scheffé montrent que la différence de moyenne entre A et B est significative au seuil de α = 10%. En revanche on n'est pas en mesure d'affirmer que B est différent de C ou que A est différent de C.

Le test de Scheffé, en théorie

Maintenant que vous avez vu comment (et pourquoi) effectuer un test de Scheffé, revenons "en arrière" pour approfondir le principe de ce test.

On considère r groupes, et l'on définit μ_i comme étant la moyenne du groupe numéro i. Un contraste se définit de la manière suivante:

     $C = \sum_{i=1}^r c_i\mu_i \\ avec \quad \sum_{i=1}^r c_i = 0$

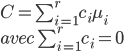
Cela signifie que si l'on a trois groupes, on peut considérer (entre autres) les contrastes suivants:

     $C_{A-B}=\mu_A-\mu_B \\ C_{A-C}=\mu_B-\mu_C \\ C_{B-C}=\mu_A-\mu_C$

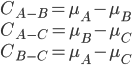
La valeur estimée d'un contraste est simplement:

     $\hat{C} = \sum_{i=1}^r c_i\bar{Y}_i$

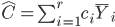
Donc les estimations des trois contrastes qui nous intéressent sont:

estimated_mu=as.vector(tapply(Y,X,"mean"))
contrasts=c(estimated_mu[1]-estimated_mu[2],
            estimated_mu[1]-estimated_mu[3],
            estimated_mu[2]-estimated_mu[3])

print(contrasts)

## [1] -2.5551 -0.8675  1.6876

La variance associée à cet estimateur est:

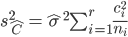
     $s_{\hat{C}}^2 = \hat{\sigma}^2\sum_{i=1}^r \frac{c_i^2}{n_i}$

Donc l'écart-type associée à chacun des trois estimateurs considérés est:

n=as.vector(tapply(Y,X,"length"))
N=sum(n)
r=3
estimated_sigma=sqrt(sum(mymod$residuals^2)/(N-r))
sigma_contrasts=c(sqrt(estimated_sigma^2*(1/n[1]+1/n[2])),
                  sqrt(estimated_sigma^2*(1/n[1]+1/n[3])),
                  sqrt(estimated_sigma^2*(1/n[2]+1/n[3])))
print(sigma_contrasts)

## [1] 1.133 1.014 1.161

Ainsi il y a une probabilité de 1 − α que C se trouve dans l'intervalle suivant:

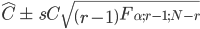
     $\hat{C}\pm \quad s_\hat{C}\sqrt{\left(r-1\right)F_{\alpha;r-1;N-r}}$

On peut donc calculer les intervalles de confiance comme suit:

alpha=0.1
delta=sigma_contrasts*sqrt(2*qf(1-alpha,3-1,length(X)-3))


results=data.frame(round(contrasts,3),
                   round(sigma_contrasts,3),
                   round(contrasts-delta,3),
                   round(contrasts+delta,3))
row.names(results)=c("A-B","A-C","B-C")
colnames(results)=c("contrast","sigma","LCI","UCI")

Par ailleurs la statistique suivante:

     $T_{Scheffe}=\frac{C^2}{(r-1)s_{\hat{C}}^2}$

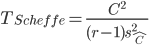
suit une loi de Fisher sous hypothèse que tous les contrastes sont nuls.

On peut donc calculer les p-values comme suit:

T_Scheffe=((contrasts^2)/(sigma_contrasts^2))/(3-1)
pvalues=1-pf(T_Scheffe, 3-1,length(X)-3)
print(data.frame(results,pvalues))

##     contrast sigma    LCI    UCI pvalues
## A-B   -2.555 1.133 -5.034 -0.076 0.08718
## A-C   -0.868 1.014 -3.087  1.352 0.69507
## B-C    1.688 1.161 -0.854  4.229 0.35448

R-atique