| Vincent Langlois | ||
| page professionnelle |
La rhéologie des mousses
Nous avons cherché à comprendre comment s'écoule une mousse. Or, si l'on connaît bien les lois physico-chimiques qui régissent le
comportement d'un film de savon ou d'une bulle, il est plus délicat de passer
à l'échelle supérieure et de prédire la dynamique d'un ensemble de plusieurs
milliers de bulles.
Divers résultats expérimentaux montrent que les mousses de savon, qu'on utilise
comme système modèle, ont une rhéologie non-linéaire de
Herschel-Bulkley, c'est-à-dire qu'il faut une contrainte minimale
pour parvenir à faire couler la mousse (en effet, au repos une
mousse est un solide élastique). Une fois ce seuil franchi, la mousse se
déforme, puis se met à couler et devient rhéo-fluidifiante: plus
elle coule vite, moins elle est
visqueuse. Comment expliquer ce comportement ?
L'approche classique pour modéliser une mousse consiste à la décrire comme un
assemblage de films de savons, dont on cherche à minimiser la surface.
Malheureusement cette méthode, si elle est fructueuse pour comprendre les
propriétés de la mousse au repos (ou en déformation quasi-statique), ne permet pas d'appréhender son comportement
dynamique. Nous avons donc adapté et complété le modèle développé par D. Durian en 1995, qui consiste à décrire
la mousse comme une empilement de bulles, de manière analogue à un milieu granulaire.
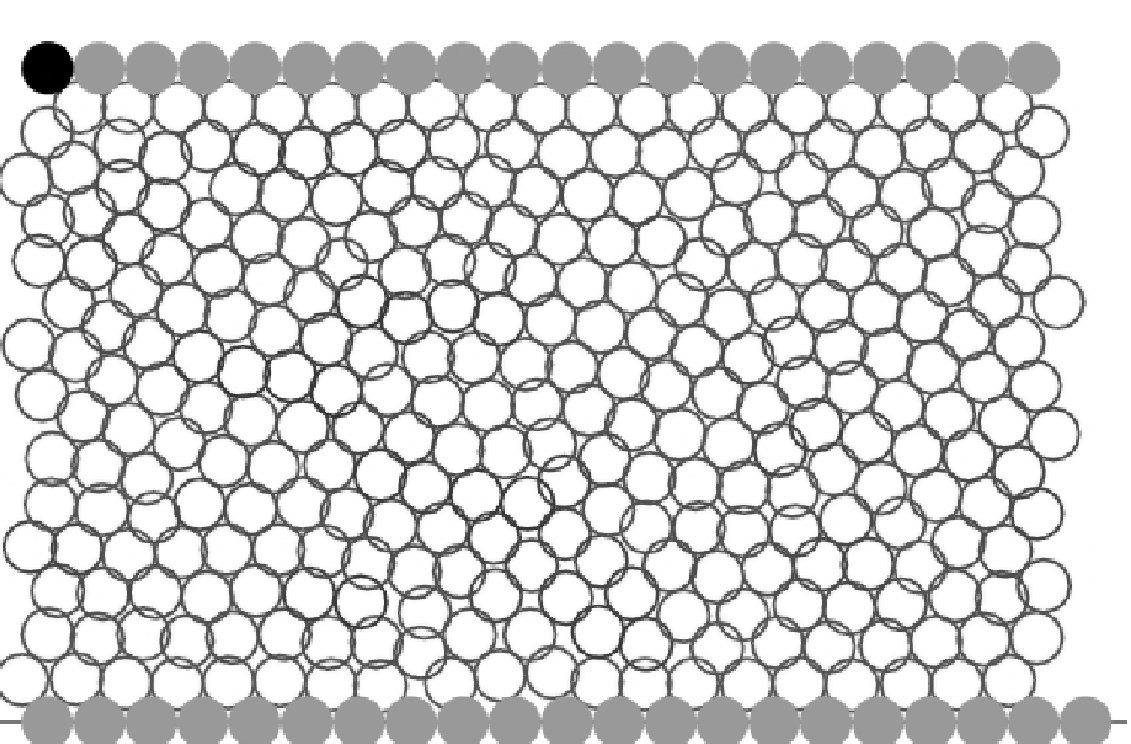
En utilisant ensuite des lois très simples pour décrire l'interaction entre deux bulles, on peut ainsi réaliser des simulations numériques de l'écoulement de plusieurs centaines ou milliers de bulles. Cette approche nous a permis de retrouver, pour la première fois à partir d'un modèle discret, la loi de Herschel-Bulkley, mais également de mieux comprendre la formation de bandes de cisaillement dans une mousse 2D s'écoulant entre deux plaques de verre. L'intérêt de ces simulations numériques est qu'il est désormais très facile de modifier les caractéristiques de base de la mousse (dispersion des tailles de bulles, fraction volumique en eau,...) et de prédire leur influence sur ses propriétés dynamiques.
Pour plus de détails, vous avez accès ici à un séminaire donné à Cambridge (IMA) en 2009.
|
© Copyright 2007-18.
Vincent Langlois
|
 |

|


