English version below
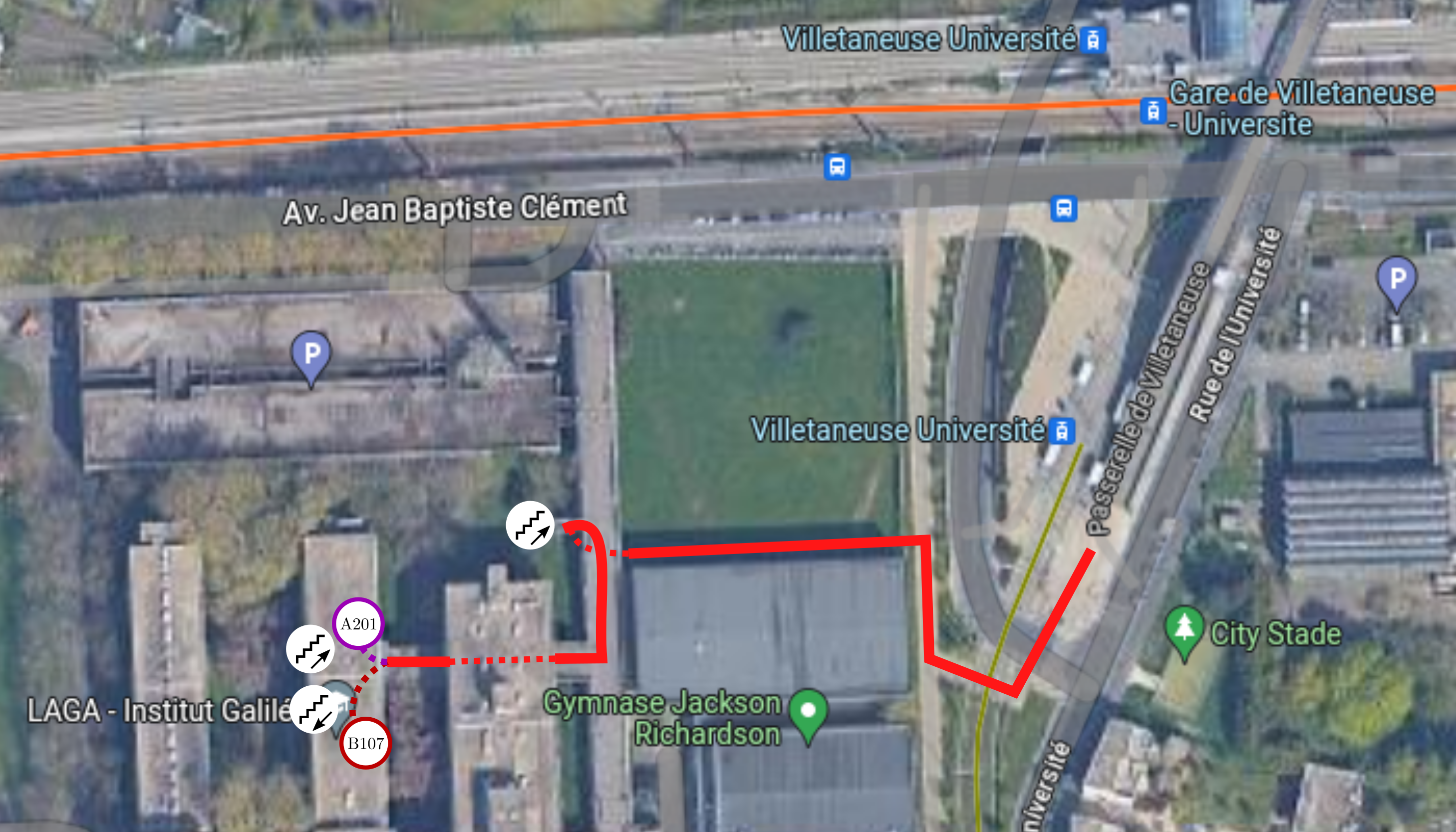
Elle sera suivie d'un pot en salle A201 (qui pourra également être diffusé en visio si besoin, ce que je déconseille vivement vu la qualité esthétique et gustative du buffet prévu).
Résumé
Comment empiler un nombre
infini d’oranges pour maximiser la proportion de l’espace couvert ?
Kepler a conjecturé que l’empilement des "balles de canon" est
optimal. 400 ans se sont écoulés avant que cette conjecture soit
démontrée par Hales et Ferguson dont la preuve comporte 6 papiers et
des dizaines de milliers de lignes de code informatique.
Comment
arranger un nombre infini de pièces de monnaie de 3 rayons différents
sur une table infinie pour maximiser la proportion de la surface
couverte ? Un arrangement de disques est dit triangulé si chacun de
ses "trous" est borné par trois disques mutuellement
tangents. Connelly a conjecturé que si de tels arrangements existent,
l’un d’eux maximise la proportion de la surface couverte; cela est
vrai pour les arrangement unaires et binaires.
Dans cette thèse, nous
étudions diverses techniques utilisées dans la preuve de la conjecture
de Kepler ainsi que dans d’autres résultats importants de le domaine
des arrangements de disques et de sphères, tels que la redistribution
de la densité locale basée sur la recherche par l’ordinateur et
l’arithmétique d’intervalles. Cela nous permet de prouver l’assertion
de la conjecture de Connelly pour 31 triplets de rayons de disques
triangulés et de la réfuter pour 45 autres triplets. En outre, nous
obtenons des bornes précises sur la densité locale des cellules
simpliciales dans les empilements à 2 sphères en 3D.
Jury
Ici vous pouvez trouver le manuscrit.
It will be followed by a reception (food and drinks) in room A201 (it can also be accessible remotely by request which I would not recommend given the aesthetic and taste quality of the planned buffet).
Abstract
How to stack an infinite
number of oranges to maximize the proportion of the covered space?
Kepler conjectured that the "cannonball" packing is an optimal way to
do it. This conjecture took almost 400 years to prove, and the proof
of Hales and Ferguson consists of 6 papers and tens of thousands of
lines of computer code.
Given an infinite number of coins of 3 fixed
radii, how to place them on an infinite table to maximize the
proportion of the covered surface? Triangulated disc packings are
those where each "hole" is bounded by three pairwise tangent
discs. Connelly conjectured that for the sets of disc radii where
triangulated packings exist, one of them maximizes the proportion of
the covered surface; this holds for unary and binary disc packings.
In this thesis, we study various techniques used in the proof of the
Kepler conjecture and other crucial results of the domain of disc and
sphere packings, such as local density redistribution based on
computer search and interval arithmetic. This allows us to prove the
statement of the Connelly conjecture for 31 triangulated triplets of
disc radii and disprove it for 45 other triplets. Besides that, we
obtain tight upper bounds on the local density of simplicial cells in
2-sphere packings in 3D.
You can find the manuscript here.
