Statistical mechanics
approaches to turbulence proved fruitful in order to
explain many phenomena. One of the key theoretical tools
are large deviation theory and kinetic theory. Using large
deviation theory we studied equilibrium
and out of equilibrium statistical mechanics of
geophysical flows, non-equilibrium
phase transitions in turbulence, and large deviation
of Reynolds stresses. Instantons
derived from large deviation theory predict most probable
transitions between attractors. Kinetic theory approaches
have been used to study the formation of atmosphere
jets and the self organization of two dimensional
turbulence. We have also studied rare
transitions and instantons for turbulent atmospheres,
for instance related to abrupt
changes of Jupiter's climate.
Turbulence and
large deviation theory: Seminar
given during the Workshop
on Instantons and Extreme Events in Turbulence
and Dynamical Systems, held at Rio de
Janeiro in December 2015 [movie]
[slides]
Large deviation theory for atmosphere jets: Seminar given during the Workshop on Instantons and Extreme Events in Turbulence and Dynamical Systems, held at Rio de Janeiro in December 2015 [movie] [slides]
Large deviation
theory and instanton predict transition paths between
turbulent attractors
The instanton of the
2D Navier-Stokes equations
In equilibrium statistical mechanics transition rates between attractors are given by Arrhenius law (chemistry, phase transitions in magnetic systems, condensed matter, bio-molecules). For complex dynamical systems like turbulent flows, large deviation theory extend the equilibrium theory. Transitions rates between attractors can be computed. Moreover transition paths are predictable as action minima (instantons). For the first time we have computed instantons related to non-equilibrium phase transitions between dipoles and parallel flows in two dimensional turbulence.
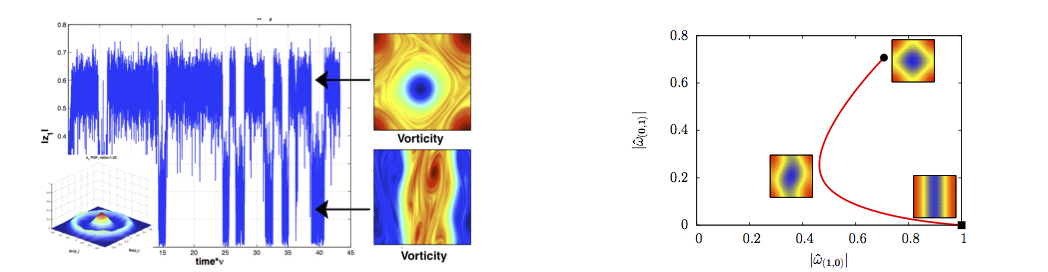
The 2D
Navier-Stokes instanton for the transition between dipoles
and parallel flows
J. LAURIE and F. BOUCHET, 2014, Computation of rare transitions in the barotropic quasi-geostrophic equations, New J. Phys. 17 (2015) 015009, [.pdf]
Instantons for
quasi-geostrophic dynamics
For quasigeostrophic models that
describe atmosphere jets, and for a special set of forces,
phase transitions and instantons can be computed
explicitly.
F. BOUCHET, J. LAURIE, and O. ZABORONSKI, 2014, Langevin dynamics, large deviations and instantons for the quasi-geostrophic model and two-dimensional Euler equations, J Stat Phys (2014) 156:1066Ė1092, and arXiv:1403.0216 [.pdf]
Equilibrium and out of equilibrium statistical mechanics of geophysical flows
In
many applications of fluid dynamics, one of the most
important problem is the prediction of the very high
Reynolds large-scale flows. The highly turbulent nature of
such flows, for instance ocean circulation or atmosphere,
renders a probabilistic description desirable. We describe
theoretical
progresses in order to use statistical mechanics
ideas for these problems and some applications
to real geophysical flows.
F. BOUCHET, and A. VENAILLE, Statistical mechanics of two-dimensional and geophysical flows, Physics Reports, 2012 [.pdf]
Recent publications on the equilibrium statistical mechanics of turbulent flows:
2) S. THALABARD, B. DUBRULLE, and F. BOUCHET, 2014, Statistical mechanics of the 3D axisymmetric Euler equations in a Taylor-Couette geometry. J. Stat. Mech.: Theory and Experiment, 1, P01005. [.pdf]
Applications of Stat. Mech. to real geophysical flows
Jupiter-Equilibrium

The
Jupiter's Great Red Spot
An
equilibrium statistical mechanics explanation of the
self-organization of geophysical flows has been proposed
by Robert-Sommeria and Miller (RSM). The RSM theory has
been successfully applied to the Jupiterís troposphere:
cyclones, anticyclones and jets have been quantitatively
described by this theory
(see:
A statistical
equilibrium model of the Great Red Spot and other Jovian
vortices and the publications Bouchet-Sommeria-2002
and Bouchet-Dumont-2002).
Ocean-Equilibrium

The see
surface height of the North Atlantic.
A
natural question is to know if some aspects of the large
scale organization of ocean dynamics, the map of currents
for instance, can be understood in the context of
equilibrium statistical mechanics.
Ocean rings are the most common vortices in oceans. They
explain most of the kinetic energy variability of ocean
dynamics. We have explained the structures, shapes, and
velocity fields of ocean rings using equilibrium
statistical mechanics. We have also explained from
statistical mechanics why the complex mixing resulting
from turbulence leads to the formation of strong mid-basin
jets like the Gulf Stream in the Atlantic Ocean and the
Kuroshio in the Pacific Ocean.
(see Equilibrium Statistical Mechanics of Mid Basin Eastward Jets and of Ocean Vortices)
Theoretical progresses in the Stat. Mech. of 2D and
geophysical flows
Out of equilibrium phase transitions

Prediction
of the bistability of turbulent flows for the 2D Navier
Stokes Equations
(please
see Out of
Equilibrium Phase Transitions in 2D and Geophysical
Flows and Bouchet-Simonnet-PRL-2009)
Classification of
phase transitions

The 2D Euler equations are an example of systems with
long range interactions. Systems with long range
interactions are not additive, which can lead to
inequivalence between the microcanonical and canonical
ensembles. The microcanonical ensemble may show richer
behavior than the canonical one, including negative heat
capacities (the temperature decrease when the energy is
increased) and other non-common behaviors like negative
temperature jumps when the energy is increased, at a
microcanonical critical point.
We have proposed a generalization of Landau classification
for systems with long range interactions that describes
all the possible phase transitions associated with
situations of ensemble inequivalence. The phenomenology
for such phase transitions is richer than the classical
one. We have then predicted new ensemble inequivalence
situations that have never been observed yet and others
than have been observed only after our work
(see Bouchet-Barre-JStatPhys-2005).
Simpler variational
problems for the RSM statistical equilibria
The Robert-Sommeria-Miller equilibrium statistical mechanics predicts the final organization of two dimensional flows. This powerful theory is difficult to handle practically, due to the complexity associated with an infinite number of constraints. Several alternative simpler variational problems, based on Casimirís or stream function functionals, have been considered recently. We have established the relations between all these variational problems, justifying the use of simpler formulations. This provides a drastic mathematical simplifications for the study of equilibria, and increases our physical insight by justifying new physical analogies.
(see Bouchet-PhysicaD-2008).
Previously unobserved phase transitions and ensemble inequivalence for academic ocean models
We propose a theoretical description for the equilibrium states of a large class of models of two-dimensional and geophysical flows. Statistical ensemble inequivalence is found to exist generically in those models, related with the occurrence of peculiar phase transitions in the flow topology. The first examples of a bicritical point in the context of systems with long range interactions is reported. Steady states of academic ocean models, the Fofonoff flows, are studied in the perspective of those results. A more detailed description is proposed in and will be the subject of the forthcoming publication.
(see Venaille-Bouchet-PRL-2009).