Ce billet vise à vous montrer comment ajuster un modèle de distribution (par exemple une jolie « cloche » gaussienne) à une distribution empirique (i.e. la distribution de vos données telle que vous l’observez, par exemple en traçant l’histogramme correspondant).

Il existe plusieurs méthodes possibles pour faire cela, dont la méthode des moments dont je vais parler ici.

Considérons les données disponibles ici

x=read.csv(paste(dat.path,"data_vraisemblance.csv",sep=""),sep=";")$x
head(x)

## [1] 132.5 194.8 179.0 108.7 112.5 160.5

L’histogramme suivant montre la distribution empirique de la variable.

hist(x, col="pink")

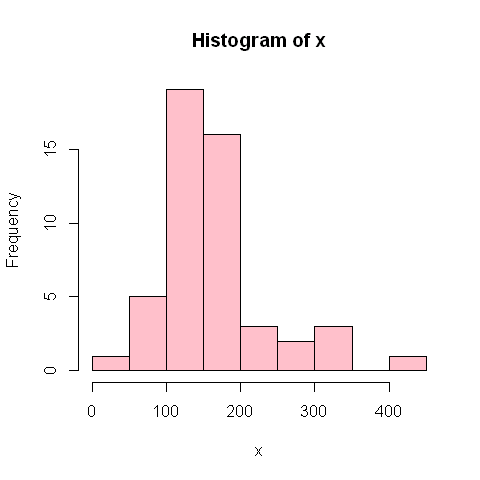
Un exemple: modèle de distribution normale

Nous allons essayer d’ajuster une loi de distribution normale (ou gaussienne) à ces données (i.e. nous allons « caler » la fameuse forme de cloche sur cette distribution).

Un modèle de distribution normale pour la variable X s’écrit ainsi:

    $$X \sim \mathcal{N}(\mu,\sigma)$$

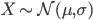
C’est à dire qu’un modèle de distribution normale a deux paramètres:

• un paramètre μ
• un paramètre σ

La définition de la loi normale est telle que son espérance et sa variance -i.e. ses moments d’ordre 1 et 2- sont:

    $$E(X)=\mu \\
      Var(X)=\sigma^2
    $$

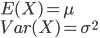
C’est à dire que l’on s’attend à ce que les données aient une moyenne proche de μ et un écart-type proche de σ (« proche de » et non « égal à » car du fait du hasard d’échantillonnage on n’observe pas exactement la valeur théorique).

Par conséquent, on peut supposer que la moyenne et l’écart-type observés constituent une estimation possible de μ et σ (estimations que l’on distingue de la valeur réelle du parmètre par un chapeau, « \^ »):

    $$\hat\mu=\bar{X}=\frac{1}{n}\sum_{i=1}^n X_i \\
       \hat\sigma=\sqrt{\frac{1}{n-1}\sum_{i=1}^n (X_i-\bar{X})^2}
    $$

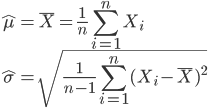
Il s’agit ici d’une estimation des paramètre par la méthode des moments

hat_mu=mean(x)
hat_sigma=sd(x)
print(hat_mu)

## [1] 166.6

print(hat_sigma)

## [1] 73.48

Une loi normale ayant une telle moyenne et un tel écart type a pour densité de probabilité:

xtheo=-100:600
ytheo=dnorm(xtheo, hat_mu,hat_sigma)

Voyons ce que nous donne cette estimation de la loi de distribution graphiquement:

hist(x, col="pink", prob=T)
points(xtheo,ytheo, col="lightslateblue",type="l", lwd=2)

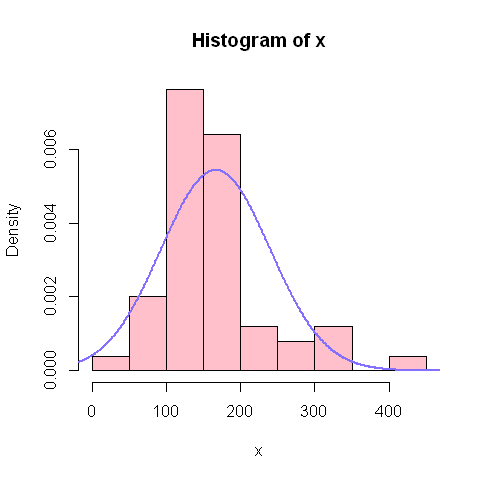
On peut aussi examiner la différence entre distribution empirique et modèle de distribution théorique à l’aide de diagrammes quantile-quantile (ou q-q plots):

quantiles_theoriques=qnorm((1:length(x))/length(x),hat_mu,hat_sigma)
qqplot(quantiles_theoriques,x)
abline(a=0,b=1, col="lightslateblue")

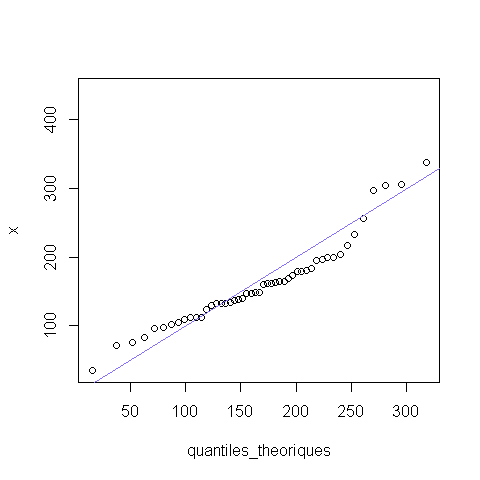
Les graphiques ci-dessus montrent que le modèle de distribution normale ne s’ajuste pas très bien aux observations. En effet, il y a une certaine asymétrie dans ces données.

Un exemple: modèle de distribution log-normale

Nous allons maintenant ajuster une loi de distribution log-normale à ces données, pour tenter de rendre compte de l’asymétrie de la distribution.

Un modèle de distribution log-normale pour la variable X s’écrit ainsi:

    $$X \sim log\mathcal{N}(\mu_l,\sigma_l)$$

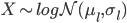
C’est à dire qu’un modèle de distribution log-normale a deux paramètres:

• un paramètre μ_l
• un paramètre σ_l

Mathématiquement (par définition de cette loi gaussienne), l’espérance et la variance (i.e. les moments d’ordre 1 et 2) d’une telle loi sont:

    $$
    E(X)=exp(\mu_l+{\sigma_l}^2/2) \\
    Var(X)=(exp(\sigma_l^2)-1)exp(2\mu_l+{\sigma_l}^2)
    $$

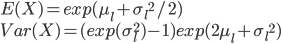
On a ainsi un système de deux équations à deux inconnues (μ_l et σ_l) qu’il est possible de résoudre, de façon à pouvoir exprimer μ_l et σ_l en fonction de l’espérance et de la variance de X.

… Bon, c’est possible, mais un peu compliqué pour qui aime rigoler. Nous allons donc ici plutôt utiliser une propriété de la loi log-normale, qui est que:

    $$X \sim log\mathcal{N}(\mu_l,\sigma_l) \Leftrightarrow log(X) \sim \mathcal{N}(\mu_l,\sigma_l)$$

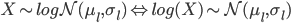
C’est à dire que l’on s’attend à ce que les données log-transformées aient une moyenne proche de μ_l et un écart-type proche de σ_l.

Par conséquent, les estimations par la méthode des moments sont:

hat_mu_l=mean(log(x))
hat_sigma_l=sd(log(x))
print(hat_mu_l)

## [1] 5.027

print(hat_sigma_l)

## [1] 0.4324

Une loi log-normale ayant ces deux valeurs de paramètres a pour densité de probabilité:

xtheo=-100:600
ytheo_l=dlnorm(xtheo, hat_mu_l,hat_sigma_l)

Voyons ce que nous donne cette estimation de la loi de distribution graphiquement(on conserve la distribution normale en bleu pour comparaison):

hist(x, col="pink", prob=T)
points(xtheo,ytheo, col="lightslateblue",type="l", lwd=2)
points(xtheo,ytheo_l, col="palevioletred",type="l", lwd=2)

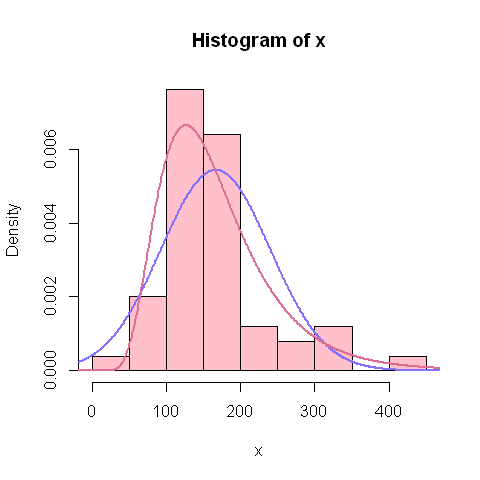
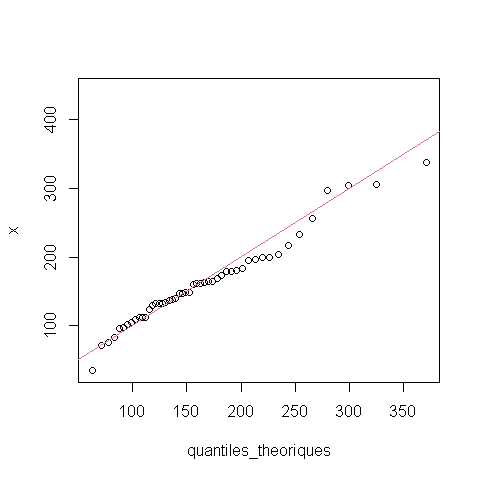
Et le diagramme quantile-quantile (ou q-q plots):

quantiles_theoriques=qlnorm((1:length(x))/length(x),hat_mu_l,hat_sigma_l)
qqplot(quantiles_theoriques,x)
abline(a=0,b=1, col="palevioletred")