Définition

L’autocorrélation (ou l’autocovariance) d’une série fait référence au fait que dans une série temporelle ou spatiale, la mesure d’un phénomène à un instant t peut être corrélée aux mesures précédentes (au temps t − 1, t − 2, t − 3, etc.) ou aux mesures suivantes (à t + 1, t + 2, t + 3, …). Une série autocorrélée est ainsi corrélée à elle-même, avec un décalage (lag) donné.

Voici la définition mathématiques de l’autocovariance et de l’autocorrélation pour une variable Xt de moyenne μ et d’écart-type σ.

Autocovariance de X pour un décalage de k:

    $$\gamma_k= E((X_t-\mu)(X_{t+k}-\mu))$$

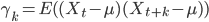
Autocorrélation de X pour un décalage de k:

    $$\rho_k=\frac{\gamma_k}{\sigma^2}$$

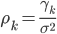
Calcul

Considérons la série suivante:

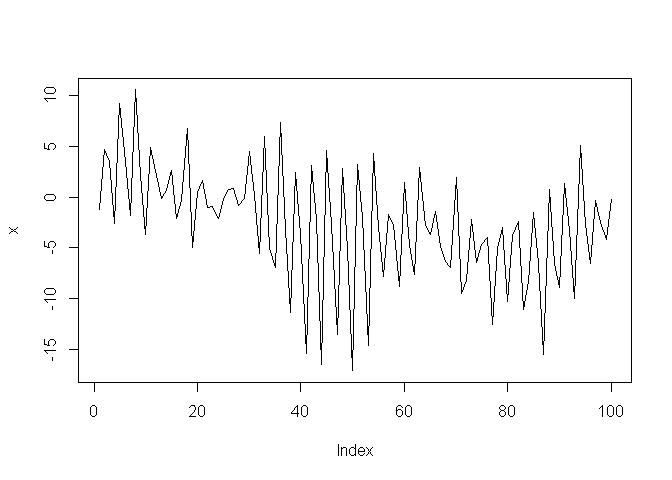
On peut calculer l’autocorrélation de la série (pour différents décalages k) de la manière suivante:

result_acf=acf(x)


print(data.frame(result_acf$lag,result_acf$acf)[1:10,])

##    result_acf.lag result_acf.acf
## 1               0    1.000000000
## 2               1   -0.058671812
## 3               2   -0.070941755
## 4               3    0.834912500
## 5               4   -0.003573716
## 6               5   -0.094295738
## 7               6    0.701497697
## 8               7    0.027054973
## 9               8   -0.143765876
## 10              9    0.585117703

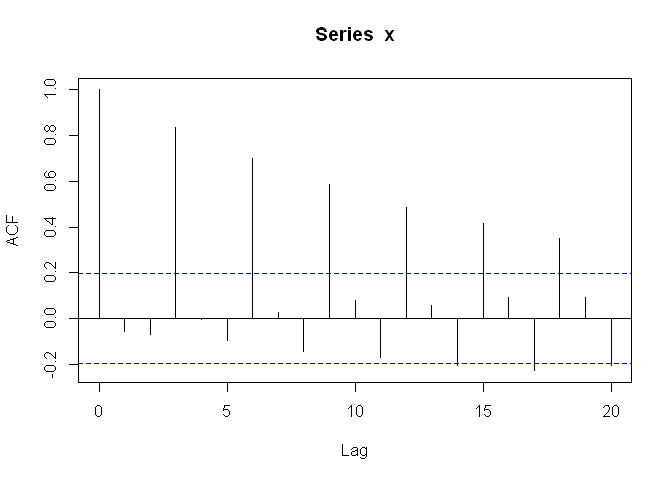
Le graphique ainsi obtenu est un corrélogramme.

L’autocorrélation est particulièrement forte pour les décalages 3, 6, et 9. (Et 0, mais ça ne signifie rien: l’autocorrélation de la série avec elle-même -sans décalage- est forcément de 1!).

Vérifions ci-après que la série est très corrélée avec elle-même pour un décalage de 3:

plot  ( 1:length(x),   x,type="l")
points((1:length(x))-3,x,type="l",col="red")

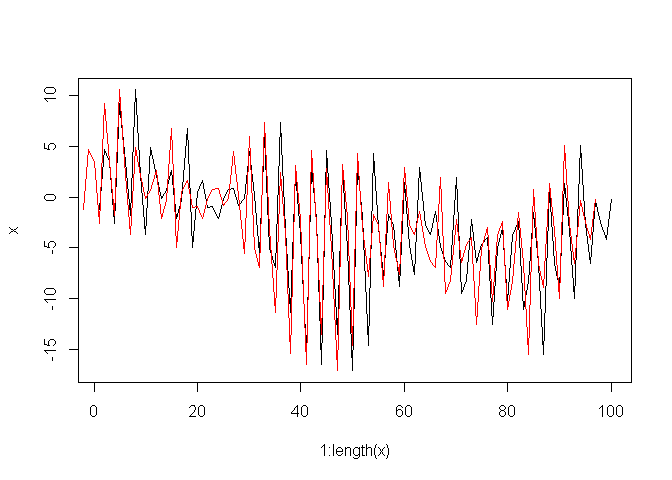
On peut retrouver les résultats de la fonction acf à la main (par exemple, ici, pour un décalage k = 3), de la manière suivante:

n=100
k=3
mu_estim=mean(x)
sigma_estim=sd(x)
x1=x[(k+1): 100   ]
x2=x[   1 :(100-k)]
gamma_k3=mean((x1-mu_estim)*(x2-mu_estim))*((n-k)/(n))
rho_k3=gamma_k3/(sigma_estim^2)
# résultat obtenu "à la main":
print(rho_k3)

## [1] 0.8265634

# résultat obtenu via l'utilisation de la fonction acf:
result_acf_k3=result_acf$acf[which(result_acf$lag==3)]
print(result_acf_k3)

## [1] 0.8349125

Significativité

La droite horizontale pointillée sur le graphique issu de la fonction « acf » nous indique le seuil critique au-delà duquel l’autocorrélation est considérée significative.

En effet, sous hypothèse d’indépendance, la corrélation croisée de deux séries X et Y (de même taille n, et de même moyenne et écart-type) sera dans 95% des cas comprise dans l’intervalle

          $$[-\frac{1.96}{\sqrt(n)},\frac{1.96}{\sqrt(n)}]$$

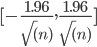
On peut le vérifier comme suit:

n=100
mu=mu_estim
sigma=sigma_estim
gamma=rep(NA,1000)
for (i in 1:1000){
  x1=rnorm(n,mu,sigma)
  x2=rnorm(n,mu,sigma)
  gamma[i]=mean((x1-mu)*(x2-mu))/(sigma^2)
}
# quantiles d'ordre 2.5% et 97.5% de gamma (x et y sont indépendants):
quantile(gamma,c(0.025,0.975))

##       2.5%      97.5% 
## -0.2073450  0.1881062

# valeur critique proposées par la fonction acf:
print(1.96/sqrt(n))

## [1] 0.196

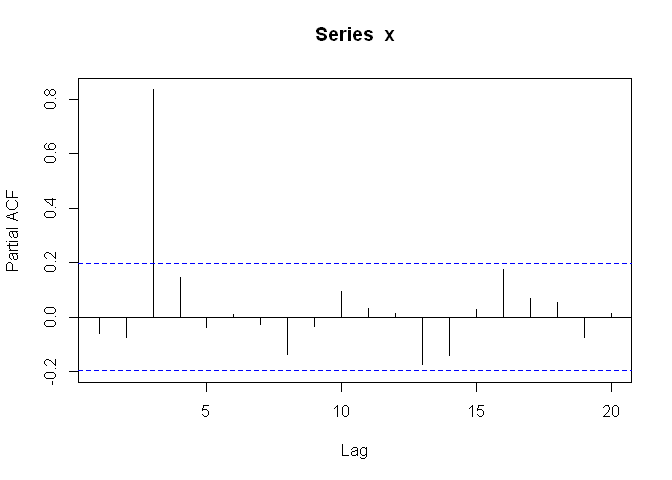
Autocorrélation partielle

Observons à nouveau le corrélogramme. On a une forte autocorrélation pour un décalage de 3, de 6, de 9… Or l’autocorrélation pour le décalage de 6 et 9 pourrait très bien être une conséquence de celle existant pour le décalage de 3.

L’autocorrélation partielle permet de mesurer l’autocorrélation d’un signal pour un décalage k « indépendamment » des autocorrélations pour les décalages inférieurs.

result_pacf=pacf(x)


print(data.frame(result_pacf$lag,result_pacf$acf)[1:10,])

##    result_pacf.lag result_pacf.acf
## 1                1    -0.058671812
## 2                2    -0.074641079
## 3                3     0.833557643
## 4                4     0.147011978
## 5                5    -0.037987995
## 6                6     0.009651406
## 7                7    -0.024764942
## 8                8    -0.134581704
## 9                9    -0.034975492
## 10              10     0.094532964

On vérifie ici que les autocorrélations observées aux décalages 6 et 9 étaient un effet résiduel de l’autocorrélation pour un décalage de 3.

Références

Pour plus de renseignements sur l’autocorrélation et (au sens très large) sur l’analyse de séries temporelles, vous pouvez vous référer à Cowpertwait and Metcalfe (2009) et Venables and Ripley (2002).

Cowpertwait, Paul S. P, and Andrew V Metcalfe. 2009. Introductory Time Series with R. New York: Springer-Verlag. http://dx.doi.org/10.1007/978-0-387-88698-5.

Venables, W. N, and Brian D Ripley. 2002. Modern Applied Statistics with S. New York: Springer. http://www.myilibrary.com?id=18937.