Qu'est-ce que c'est?

Les arbres décisionnels font partie des méthodes d'apprentissage supervisé, et font à ce titre partie de la boîte à outils du parfait petit dataminer. Ils visent à prédire les valeurs prises par une variable en fonction d'un jeu de variables d'entrée (qu'on appellera ici les descripteurs). Cette prédiction se fait à travers la construction d'un arbre dont chaque noeud correspond à une décision quant à la valeur de la variable à prédire. Cette décision est prise en fonction de la valeur d'un des descripteurs.

La variable à prédire et les descripteurs, peuvent être quantitatifs ou catégoriels.

Exemple:

Considérons l'exemple suivant (purement fictif):

On imagine que le propriétaire d'un magasin de vêtements a noté tous les articles disponibles selon leur prix, leur qualité (note de 0 à 100), leur branchitude (note de 0 à 100) et leur flashitude (note de 0 à 100). Il note si ces articles ont été achetés par des clients au cours de la semaine passée.

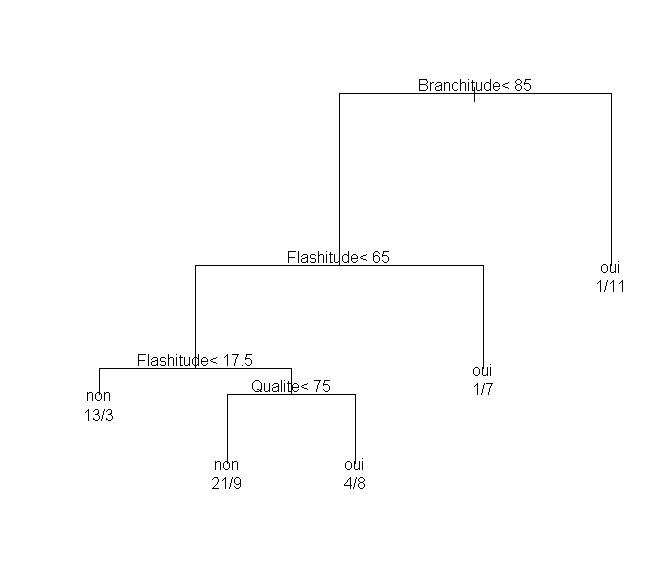
L'arbre de classification ci-dessus s'interprète de la manière suivante.

Si la valeur de branchitude d'un article est supérieure à 85, alors les clients l'achètent (11 achats contre 1 non-achat).

Si la branchitude d'un article est inférieure à 85 mais sa flashitude est supérieure à 65, alors les clients l'achètent (7 achats contre un non-achat).

Si la branchitude d'un article est inférieure à 85, et sa flashitude inférieure à 17.5, alors les clients ne l'achètent pas (13 non-achats contre 3 achats). Si la branchitude est inférieure à 65, la flashitude entre 17.5 et 65, mais la qualité est bonne (supérieure à 75), alors les clients l'achètent tout de même (8 achats contre 4 non-achats). Si au contraire la qualité de l'article est médiocre (inférieure à 75), alors les clients ne l'achètent pas (21 non achats contre 9 achats).

(En résumé, si j'étais le gérant de ce magasin, pour maximiser mes ventes, j'essaierais de proposer des articles branchés et flashy, et préférentiellement de bonne qualité, sans trop me soucier du prix auquel je les affiche...)

Construction d'un arbre de décision

Nous allons voir maintenant comment construire cet arbre. Le jeu de données évoqué ci-dessus se trouve ici.

Pour calculer l'arbre de décision, nous allons utiliser le package rpart.

magasin=read.table(paste(dat.path,"magasin.csv",sep=""),
                   sep=";", header=T, dec=",")
attach(magasin)
dt=rpart(Achat~Prix+Flashitude+Branchitude+Qualite, data=magasin)

Le graphique ci-dessus est généré à travers les commandes suivantes:

plot(dt)
text(dt, use.n=T)

Examinons l'objet renvoyé par la fonction rpart.

print(dt)

## n= 78 
## 
## node), split, n, loss, yval, (yprob)
##       * denotes terminal node
## 
##  1) root 78 38 non (0.51282 0.48718)  
##    2) Branchitude< 85 66 27 non (0.59091 0.40909)  
##      4) Flashitude< 65 58 20 non (0.65517 0.34483)  
##        8) Flashitude< 17.5 16  3 non (0.81250 0.18750) *
##        9) Flashitude>=17.5 42 17 non (0.59524 0.40476)  
##         18) Qualite< 75 30  9 non (0.70000 0.30000) *
##         19) Qualite>=75 12  4 oui (0.33333 0.66667) *
##      5) Flashitude>=65 8  1 oui (0.12500 0.87500) *
##    3) Branchitude>=85 12  1 oui (0.08333 0.91667) *

Voici comment lire cette sortie :

• A la racine de l'arbre (branche 1) il y a 78 individus, dont seulement 38 "oui". C'est donc le "non" qui l'emporte (à 51.3%).
• L'arbre présente un noeud qui se divise en deux branches (les branches 2 et 3). La branche 2 correspond aux individus tels que Branchitude < 85. Il y a 66 individus dans cette branche, dont seulement 27 "oui". C'est donc le "non" qui l'emporte (à 59%). La branche 3 correspond au reste des individus (tels que Branchitude  ≥  85). Il y a 12 individus dans cette branche, dont 1 seul "non". C'est donc le oui qui l'emporte (à 91.6%).
• La branche 2 présente à son tour un noeud, qui se divise en deux branches (les branches 4 et 5). La branche 4 correspond aux individus tels que Flashitude < 65. Il y a 58 individus dans cette branche dont seulement 20 "oui". C'est donc le "non" qui l'emporte (à 65%). La branche 5 correspond au reste des individus (tels que Flashitude  ≥  65). Il y a 65 individus dans cette branche dont seulement 8 "non". C'est donc le "oui" qui l'emporte (à 87.5%).
• etc.

Comment ça marche?

Dans cette partie je vais expliquer comment sont établis les critères de décision abordés ci-dessus. L'arbre de décision est créé de sorte que chaque noeud divise un ensemble d'individus en deux sous-ensembles (correspondant aux 2 branches) les plus homogènes possibles en terme de variable à prédire.

Pour calculer l'hétérogénéité d'un ensemble d'individus, on a recours à une mesure appelée impureté.

Calcul de l'impureté

Pour quantifier l'impureté d'un échantillon (i.e. son hétérogénéité en termes de classes), on utilise une fonction, dite index de Gini.

(NB: tous les codes dans cette sous-partie ne sont pas à reproduire pour construire un arbre décisionnel, ils servent simplement à illustrer la manière dont l'arbre se construit, étape par étape!)

L'index de Gini s'applique à une probabilité (par exemple probabilité d'une classe i, p_i):

    $Gini(p_i)=p_i(1-p_i)$

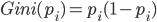
Plus la probabilité d'une classe i est proche de 0.5, (i.e. plus l'échantillon semble hétérogène pour la classe i), et plus l'index de Gini est élevé.

Pour calculer l'impureté d'un échantillon, on somme les indices de Gini pour l'ensemble des classes.

calcul_impurete=function(x){
  probas=table(x)/length(x)
  impurete=sum(probas*(1-probas))
  return(impurete)
}

probas=table(Achat)/length(Achat)
impurete=calcul_impurete(Achat)

Considérons l'ensemble des données. On a 51.2821% de classe "non" et 48.7179% de classe "oui". Cela correspond à une impureté de 0.4997.

Calcul de la réduction d'impureté

Chacun des noeuds de l'arbre est construit de manière à représenter la plus grande réduction d'impureté possible. C'est-à-dire que l'on cherche la variable et le seuil qui vont maximiser la différence entre l'impureté de la branche-parent (A) et l'impureté des branches-enfants (à gauche -L- et à droite -R-):

    $\Delta I=pr(A)I(A)-pr(A_L)I(A_L)-pr(A_R)I(A_R)$

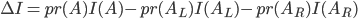
où pr(A) correspond à la probabilité de la branche A.

Considérons ainsi le premier noeud de l'arbre ci-dessus.

Nous avons vu que l'impureté pour la branche principale de l'arbre était:

prA=1
IA=calcul_impurete(Achat)
print(IA)

## [1] 0.4997

Considérons le descripteur ("Branchitude") et le seuil (85) indiqués par l'arbre de décision calculé par la fonction rpart:

n=length(Achat)
indL=which(Branchitude<85)
indR=which(Branchitude>=85)
prL=length(indL)/n
prR=length(indR)/n
IL=calcul_impurete(Achat[indL])
IR=calcul_impurete(Achat[indR])

perte_impurete=prA*IA-prL*IL-prR*IR
print(perte_impurete)

## [1] 0.06708

Cette valeur de perte d'impureté est la valeur maximale que l'on puisse obtenir pour le premier noeud, parmi tous les descripteurs et tous les seuils possibles.

Pour vous en convaincre, vous pouvez tester quelques autres possibilités (nous n'allons pas toutes les tester ici...)

Considérons par exemple ce qu'on obtiendrait avec une autre valeur de seuil (65 au lieu de 85):

prA=1
indL=which(Branchitude<65)
indR=which(Branchitude>=65)

prL=length(indL)/n
prR=length(indR)/n
IL=calcul_impurete(Achat[indL])
IR=calcul_impurete(Achat[indR])

perte_impurete=prA*IA-prL*IL-prR*IR
print(perte_impurete)

## [1] 0.0158

ou encore, considérons un autre descripteur, par exemple, la "Flashitude":

prA=1
indL=which(Flashitude<65)
indR=which(Flashitude>=65)

n=length(Achat)
prL=length(indL)/n
prR=length(indR)/n
IA=calcul_impurete(Achat)
IL=calcul_impurete(Achat[indL])
IR=calcul_impurete(Achat[indR])

perte_impurete=prA*IA-prL*IL-prR*IR
print(perte_impurete)

## [1] 0.0501

Dans ces deux cas, la perte d'impureté est effectivement moindre que celle correspondant à la sortie du modèle (ouf!).