R-atique

Les hypothèses du modèle linéaire

Beaucoup de personnes, lorsqu’elles souhaitent utiliser un modèle linéaire classique (régression linéaire ou ANOVA), se retrouvent confrontées au problème du non-respect des hypothèses de ce modèle.

En effet, les hypothèses du modèle sont les suivantes:

• distribution gaussienne des résidus
• homoscedasticité des résidus (i.e. les résidus ont la même variance quel que soit le groupe considéré, ou quelle que soit la valeur de la variable explicative considérée)

Autrement dit, si on travaille sur des données comme ça, tout va bien: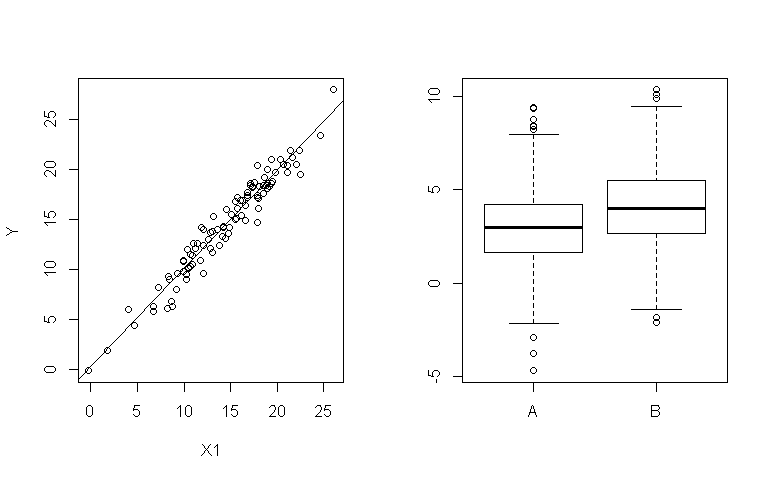

En revanche, si on travaille sur des données comme ça, les hypothèses ne sont a priori pas respectées, et tout pourrait aller mal…

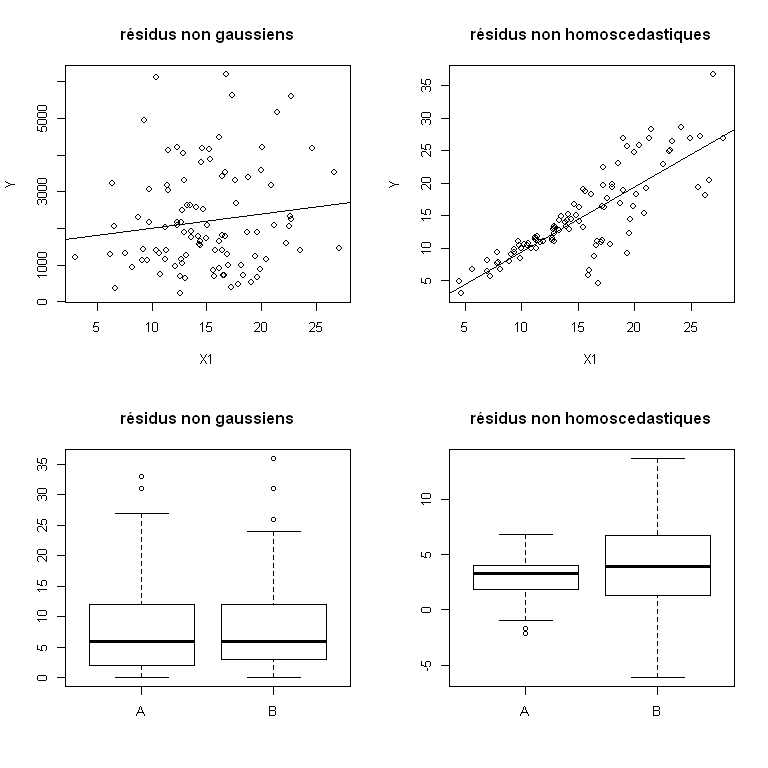
Robustesse du modèle linéaire

En fait, même si les hypothèses du modèle linéaire ne sont pas respectées, il se pourrait que tout aille bien tout de même (ouf!). La raison à cela, c’est que, comme on dit, le modèle linéaire est robuste, c’est-à-dire que sous réserve qu’il y ait une taille d’échantillon suffisante, les résultats du modèle linéaire restent valables. En termes matheux, on parle de propriétés asymptotiques (i.e. des propriétés valables si n, la taille d’échantillon « tend vers l’infini »…).

Tester les hypothèses… une mauvaise idée!!

Alors, comment savoir si tout va bien ou tout va mal, si l’application du modèle linéaire à ses données est possible ou pas?

Les « bons élèves » vont la plupart du temps essayer (avec beaucoup de diligence et de bonne volonté) de tester les hypothèses du modèle. Ils testeront la normalité des résidus avec un test comme le test de Shapiro-Wilk, ils testeront l’homoscédasticité des résidus avec un test comme le test de Fisher-Snedecor.

Dans la plupart des cas, les tests leur révéleront que les résidus ne sont ni gaussiens, ni homoscédastiques. Plus précisément, ni exactement gaussiens, ni exactement homoscédastiques… Et donc, ils se retrouveront piégés, ne pouvant ou n’osant pas braver le scandale en appliquant un modèle linéaire à ces données.

Sauf que, en vrai, l’application du modèle linéaire n’exige pas un respect exact des hypothèses, mais un respect approximatif (cf le paragraphe ci-dessus concernant la robustesse de ce modèle). Il vaut donc mieux éviter de tester le respect exact des hypothèses (au risque -très grand- de se retrouver coincé par excès de zèle) et tenter de vérifier l’applicabilité du modèle d’une autre manière…

Alors qu’est-ce qu’on fait?

Reprenons donc Les propriétés asymptotiques de l’ANOVA signifient que plus on a de données à disposition, plus l’ANOVA est capable de supporter un écart important aux hypothèses… Le problème étant évidemment qu’il y a mille et une manière de s’écarter des hypothèses et que du coup on a pas vraiment de « seuil magique » en terme de nombre de données qui permette de dire « c’est pas gaussien/c’est pas homoscedastique, mais on s’en fiche ». C’est bien là que le bât blesse. Le Chercheur qui, dans l’espoir fou d’accéder à la Vérité, se soumet dans la douleur à l’exercice ingrat et complexe des statistiques, s’exaspère: à quoi ça sert d’essayer d’être rigoureux si, au final, on se retrouve à estimer, au pifomètre, si on peut appliquer l’ANOVA ou pas?

Quand j’étais jeune et étudiante, mes professeurs de stats (pour éviter sans doute que nous soyions trop perdus ou dégoûtés par cette rigueur hasardeuse -bel oxymore, n’est-il pas?-) essayaient parfois de nous fournir un petit point de repère qui était: « Si il y a plus de 30 individus dans l’échantillon (ou par groupe), alors même si les hypothèses ne sont pas respectées on peut appliquer les résultats du modèle linéaire ».

Evidemment, c’est un point de repère un petit peu arbitraire, et un petit peu -possiblement du moins- faux (si les hypothèses ne sont vraiment pas du tout respectées, 30 individus n’y suffiront pas). MAIS ça a le mérite d’essayer de donner un ordre de grandeur.

Essayons donc, concrètement, d’aller un peu plus loin (à travers quelques exemples simulés) pour apprécier les effets d’un écart aux hypothèses sur les résultats d’un modèle linéaire, et pour apprécier quelle grandeur d’échantillon permet de pallier à cet écart…

Simulations: erreur de type I d’une ANOVA dont les résidus sont non homoscédastiques

Imaginons que l’on s’intéresse à ces données.

Je veux tester la différence de moyenne de Y entre les groupes définis par X:

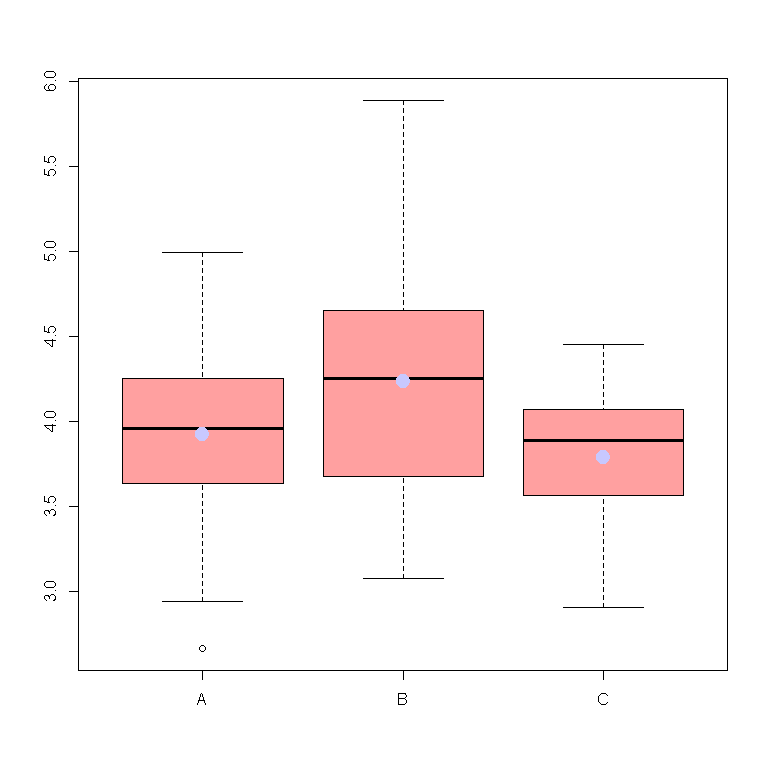
Si l’on teste l’effet du groupe (X) sur la variable Y à travers une ANOVA, alors on est amené à conclure à un effet significatif:

mod=lm(data$Y~data$X)
anova(mod)

## Analysis of Variance Table
## 
## Response: data$Y
##            Df Sum Sq Mean Sq F value Pr(>F)   
## data$X      2   3.77   1.884    6.34 0.0025 **
## Residuals 103  30.62   0.297                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Faisons un essai, et testons le respect des hypothèses de normalité et d’homoscedasticité des résidus:

shapiro.test(mod$residuals)

## 
##  Shapiro-Wilk normality test
## 
## data:  mod$residuals
## W = 0.9917, p-value = 0.7646

bartlett.test(mod$residuals,X)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  mod$residuals and X
## Bartlett's K-squared = 14.87, df = 2, p-value = 0.00059

Le test de Shapiro-Wilkes n’amène pas à rejeter l’hypothèse de normalité. En revanche, d’après le test de Bartlett, il y a des différences significatives de variance entre les groupes.

Si on s’en tenait strictement à ces résultats, donc, on pourrait renoncer à utiliser l’ANOVA pour analyser l’effet du groupe X sur Y.

Pour savoir si l’on peut utiliser l’ANOVA dans ce cas malgré l’héteroscedasticité des résidus, donc, on en vient à se poser la question suivante: Est-ce que l’écart aux hypothèses du modèle est tel que la taille d’échantillon ne parvient pas à compenser cet écart? Ou au contraire peut-on tout de même utiliser l’ANOVA?

En fait, ce dont on veut être sûr lorsque l’on utilise l’ANOVA, c’est (la plupart du temps), qu’on ne va pas affirmer qu’il existe une différence de moyenne entre les groupes alors qu’en fait cette différence pourrait être simplement due au hasard de l’échantillonnage. C’est à dire qu’on veut limiter les risques de dire « il y a un effet » alors qu’il n’y en a pas. Autrement dit, on veut limiter les risques d’erreur de type I.

Lorsque l’on utilise les résultats du test de l’ANOVA, on rejette l’hypothèse nulle (selon laquelle X n’a pas d’effet sur Y) si la p-value issue de l’ANOVA est inférieure à un certain seuil α. Dans un cas « idéal » (c’est-à-dire quand l’ANOVA « fonctionne bien »), le risque d’erreur de type I est égal à cette valeur α. Autrement dit, en décidant de rejeter l’hypothèse nulle en deça de (par exemple) α = 5% on escompte avoir une probabilité de 5% seulement de se tromper en concluant à un effet en fait inexistant.

Dans un cas non-idéal (en cas de non-respect des hypothèses, et quand les tailles d’échantillon sont insuffisantes), le risque d’erreur de type I peut en fait être plus important (ou plus faible!) que la valeur escomptée α (cette valeur escomptée est dite valeur nominale) .

Vérifions, à travers des simulations, l’égalité (à quelques variations -liées à l’aléas d’échantillonnage- près) entre valeur nominale de α et risque d’erreur de type I dans un cas « idéal ». Pour ce faire, je vais simuler 10000 jeux de données tels que :

• la moyenne de Y soit la même dans tous les groupes (hypothèse nulle vraie)
• la distribution de Y par groupe soit normale (hypothèse de distribution gaussienne vraie)
• la variance de Y soit la même dans tous les groupes (hypothèse d’homoscedasticité vraie)

n=table(X)              ## les effectifs par groupe
mu=c(3.9,3.9,3.9)       ## les moyennes par groupe   
sigma=c(0.6,0.6,0.6) ## les variances par groupe

pval1=rep(NA,10000)
for (k in 1:10000){
     Y=c(rnorm(n[1],mu[1],sigma[1]),
         rnorm(n[2],mu[2],sigma[2]),
         rnorm(n[3],mu[3],sigma[3]))
     myaov=anova(lm(Y~X))
     pval1[k]=myaov$"Pr(>F)"[1]  
}

risque_cas_ideal=length(which(pval1<=0.05))/length(pval1)
print(risque_cas_ideal)

## [1] 0.0487

On conclut bien à une différence significative de moyenne entre les groupes (alors que ces moyennes sont en fait les mêmes) dans seulement environ 5% des cas.

Vérifions maintenant, toujours à travers des simulations, l’écart entre valeur nominale de α et risque d’erreur de type I dans un cas « problématique ». Pour ce faire, je vais simuler 10000 jeux de données tels que :

• la moyenne de Y soit la même dans tous les groupes (hypothèse nulle vraie)
• la distribution de Y par groupe soit normale (hypothèse de distribution gaussienne vraie)
• la variance de Y soit légèrement différente entre les groupes (hypothèse d’homoscedasticité fausse)

Cette situation problématique est paramétrée pour générer des jeux de données « proches » de celui auquel nous avons affaire…

n=table(X)              ## les effectifs par groupe
mu=c(3.9,3.9,3.9)       ## les moyennes par groupe   
sigma=c(0.5,0.7,0.4)    ## les variances par groupe        

pval2=rep(NA,10000)
for (k in 1:10000){
     Y=c(rnorm(n[1],mu[1],sigma[1]),
         rnorm(n[2],mu[2],sigma[2]),
         rnorm(n[3],mu[3],sigma[3]))
     myaov=anova(lm(Y~X))
     pval2[k]=myaov$"Pr(>F)"[1]  
}

risque_cas_problematique=length(which(pval2<=0.05))/length(pval2)
print(risque_cas_problematique)

## [1] 0.0535

Au final, au vu des effectifs et des gammes de valeur pour la moyenne et la variance par groupe, l’écart aux hypothèses du modèle linéaire n’entraîne pas un risque d’erreur de type I (environ 5%) tellement plus important que le risque nominal…

Si j’avais des tailles d’échantillon plus grandes encore (ici environ quatre fois plus importantes), alors j’aurais a priori un risque d’erreur de type I encore plus proche de la valeur nominale de 5%:

n=c(150,150,150)        ## les effectifs par groupe
X=c(rep("A",n[1]),
    rep("B",n[2]),
    rep("C",n[3]))
mu=c(3.9,3.9,3.9)    ## les moyennes par groupe   
sigma=c(0.5,0.7,0.4) ## les variances par groupe        

pval3=rep(NA,10000)
for (k in 1:10000){
     Y=c(rnorm(n[1],mu[1],sigma[1]),
         rnorm(n[2],mu[2],sigma[2]),
         rnorm(n[3],mu[3],sigma[3]))
     myaov=anova(lm(Y~X))
     pval3[k]=myaov$"Pr(>F)"[1]  
}

risque_cas_problematique_2=length(which(pval3<=0.05))/length(pval3)
print(risque_cas_problematique_2)

## [1] 0.0535

On pourrait multiplier ce genre de simulations à l’envi… pour tester par exemple, l’effet d’effectifs très inégaux dans les groupes, ou l’effet d’un groupe avec un effectif très bas, etc.

Références

A la suite de la publication de ce billet, plusieurs personnes m’ont demandé dans les commentaires quelles étaient mes sources…

Ce que j’écris dans cet article est le fruit de lectures de thèse (en biostatistique, sur des questions étroitement reliées) et de nombreuses expérimentations (tirages aléatoires suivant divers « modèles » et analyse des conséquences sur les tests statistiques usuels, comme dans l’article). Je n’ai pas de référence bibliographique majeure à mettre en avant puisque c’est une sorte de synthèse entre expérimentation personnelle et littérature grise.

Je comprends le besoin qu’éprouveront certains (parfois à la demande de reviewers…) de justifier leur propos par un article qui ferait argument d’autorité mais ce que j’explique dans cet article est censé faire partie d’un savoir commun et reconnu (je ne suis pas nécessairement d’accord avec cela, mais pour avoir essayé en vain de publier des articles scientifiques plus ou moins sur ce sujet je sais que les statisticiens trouvent ça trop basique et que les non-statisticiens trouvent ça trop statistique :-p ).

Je vous encourage donc à citer directement cet article de blog (si citer un blog, et en français en plus, ne vous semble pas problématique d’un point de vue de l' »apparence de sérieux » -mais ne nous lançons pas dans des considérations qui pourraient nous emmener trop loin-)!…

Citation

Merci de citer ce billet de la manière suivante:

Vaudor L (2015). “Non-respect des hypothèses du modèle linéaire (ANOVA, régression): c’est grave, docteur??” .

@misc{vaudor_hypotheses_modele_lineaire, type = {blog}, title = {Non-respect des hypothèses du modèle linéaire ({ANOVA}, régression): c’est grave, docteur??}, url = {http://perso.ens-lyon.fr/lise.vaudor/non-respect-des-hypotheses-du-modele-lineaire-anova-regression-cest-grave-docteur//}, journal = {R-atique: Analyse de données avec R}, author = {Vaudor, Lise}, month = jan, year = {2015} }