Dans ce billet, je souhaite montrer comment estimer l’incertitude associée à l’estimation des paramètres (pente et ordonnée à l’origine) d’un modèle de régression linéaire simple. Pour ce faire, je vais:

• montrer comment le calcul d’incertitude dérive de résultats analytiques (i.e. d’équations qui permettent, si on le souhaite, de calculer l’incertitude « à la main »),
• fournir les lignes de code permettant de calculer (et représenter) ce même résultat sous R,
• illustrer (pour l’intervalle de confiance autour de la pente) l’origine de cette incertitude par des simulations

La régression linéaire simple: modèle, ajustement du modèle

Considérons un modèle de régression simple:

    $$Y=aX + b + E_r$$

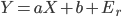
où:

• X est la variable explicative
• Y est la variable à expliquer
• a est le paramètre de pente de la régression
• b est le paramètre d’ordonnée à l’origine de la régression
• E_r est l’erreur résiduelle

Le modèle de régression simple repose sur une hypothèse de distribution normale pour l’erreur résiduelle E_r:

    $$E_r \sim \mathcal{N}(0,\sigma_r)$$

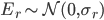
Considérons un jeu de données d’exemple. Pour être sûre que ces données suivent une loi de régression, et pour connaitre exactement les vrais paramètres de cette loi, je vais en fait les simuler:

n=15        # taille de l'échantillon
sigma_x=4.56  # variabilité de X
sigma_r=2.67  # variabilité des résidus
a=3.44        # paramètre "vrai" de pente
b=1.33        # paramètre "vrai" d'ordonnéee à l'origine

## Simulation de valeurs pour X:
X=rnorm(n,3,sigma_x)
## Simulation de valeurs pour l'erreur résiduelle:
E_r=rnorm(n,0,sigma_r)
## Simulation de valeurs pour Y:
Y=a*X+b+E_r

Je sais donc exactement comment X et Y ont été générées, et quelles sont les valeurs réelles des paramètres de la loi de régression…

Cependant, je vais maintenant faire comme si je n’en savais rien, afin de pouvoir, in fine, comparer les valeurs estimées des paramètres à leurs vraies valeurs.

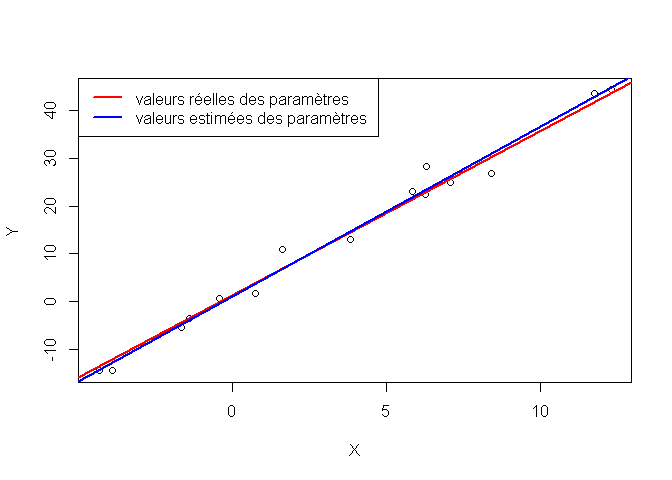
Voici comment ajuster un modèle de régression simple sous R (et estimer les valeurs de paramètres):

reg=lm(Y~X)
a_est=reg$coeff[[2]]  
b_est=reg$coeff[[1]]

print(c(a,a_est))

## [1] 3.440 3.423

print(c(b,b_est))

## [1] 1.33 1.44

On obtient bien des estimations de a et b proches quoique différentes des valeurs réelles du fait du hasard d’échantillonnage.

plot(X,Y)
abline(b,a, col="red", lwd=2)
abline(b_est,a_est,col="blue", lwd=2)
legend("topleft",
       c("valeurs réelles des paramètres", "valeurs estimées des paramètres"), 
       col=c("red","blue"),
       lwd=2)

Incertitude autour du paramètre de pente, a

Calcul analytique

Voici comment se calcule analytiquement l’incertitude autour de paramètre de pente:

Soit A la variable aléatoire correspondant à la valeur de pente estimée. La valeur observée de A est a.

La variance de A est:

    $$s_a^2=\frac{s_r^2}{n \sigma_x^2}$$

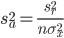
Par ailleurs, si l’on définit la variable aléatoire

    $$T=\frac{a-A}{s_a}$$

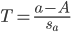
alors T suit une loi de Student à ν = n − 2 ddl.

On peut donc calculer un intervalle de confiance d’ordre 1 − α pour la pente:

    $$IC=[a-t_{1-\alpha/2}s_a, a + t_{1-\alpha/2}s_a]$$

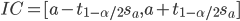
Le principe de ce calcul est en quelque sorte le suivant: à partir des hypothèses du modèle, on est en mesure de prédire (par un raisonnement mathématique) comment la la variable aléatoire correspondant à la pente estimée se distribue autour de la pente réelle. C’est à partir de cette distribution que l’on peut proposer un intervalle de confiance pour la valeur de pente.

Vérification par simulations

Vérifions ci-après le calcul de la variance de A en tirant 1000 fois au hasard une variable E_r conforme au modèle:

# Variance réelle de A
s_a=sqrt((sigma_r^2)/(n*sigma_x^2))
print(s_a)

## [1] 0.1512

# Variance estimée de A
s_a_est=sqrt((sd(reg$residuals)^2)/((n-1)*sd(X)^2))
print(s_a_est)

## [1] 0.1533

s_a_est=sqrt(((sd(reg$residuals)*((n-1)/n))^2)/(n*(sd(X)*((n-1)/n))^2))
print(s_a_est)

## [1] 0.1481

# Variance de A illustrée par des simulations
v_A=rep(NA,1000)
for (i in 1:1000){
    E=rnorm(n,0,sigma_r)
    Y=a*X+b+E
    mylm_tmp=lm(Y~X)
    v_A[i]=mylm_tmp$coeff[2]
}
s_a_sim=sd(v_A) 
print(s_a_sim)

## [1] 0.1551

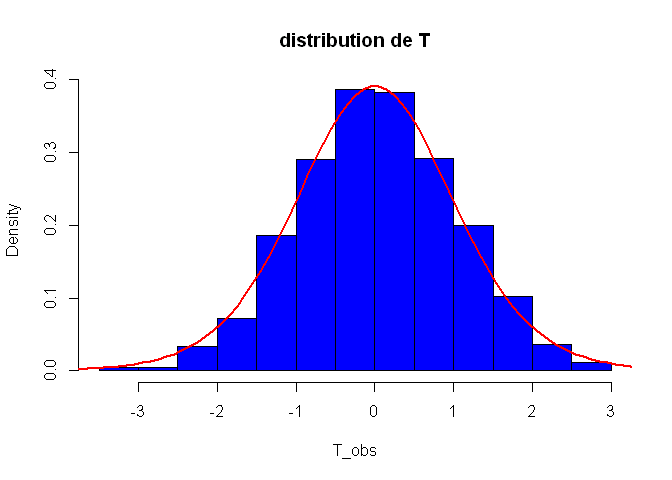
Vérifions que la variable T suit bien une loi de Student à n − 2 degrés de liberté:

T_obs=(a-v_A)/s_a_sim
hist(T_obs, col="blue", freq=F, main="distribution de T", breaks=20)
# Distribution théorique de la variable T:
T_theo=pt(seq(-10,10,by=0.1),df=n-2)
T_theo=diff(T_theo)/0.1
points(seq(-9.95,9.95,by=0.1),T_theo, type="l", col="red", lwd=2)

Calculons alors l’intervalle de confiance pour α = 0.05:

IC_a_inf=a_est-qt(0.975,n-2)*s_a_est
IC_a_sup=a_est+qt(0.975,n-2)*s_a_est
print(c(IC_a_inf,IC_a_sup))

## [1] 3.103 3.743

Comparons ce résultat à celui renvoyé par la fonction confint de R, fonction « clés en main » pour le calcul des intervalles de confiance autour des paramètres de régression:

confint(reg)

##               2.5 % 97.5 %
## (Intercept) -0.4405  3.321
## X            3.0793  3.766

Le résultat est bien le même… à quelques différences d’arrondi et de calcul de variance près… Ouf!

Vous constatez ici qu’il est bien plus simple d’obtenir ce résultat sous R en utilisant les fonctions disponibles, que de le calculer à la main (et encore bien plus que de comprendre d’où il sort, quand on n’a pas les bases en maths pour ça!). C’est à la fois la force et la faiblesse de R… ses fonctions vous facilitent la vie en vous procurant des résultats simplement… mais encore faut-il être bien sûr de comprendre de quoi il retourne pour ne pas faire des erreurs d’interprétation.

Incertitude autour du paramètre d’ordonnée à l’origine, b

Intéressons-nous maintenant au deuxième paramètre de la régression, celui correspondant à l’ordonnée à l’origine.

Calcul analytique

Voici comment calculer analytiquement l’incertitude autour de ce paramètre (on retrouve exactement le même type de raisonnement que pour la pente):

Soit B la variable aléatoire correspondant à la valeur d’ordonnée à l’origine estimée. La valeur observée de B est b.

La variance de B est:

    $$s_b^2=s_r^2\left(\frac{1}{n}+\frac{\bar(x)^2}{n \sigma_x^2}\right)$$

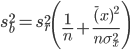
Par ailleurs, si l’on définit la variable aléatoire

    $$T=\frac{b-B}{s_b}$$

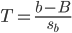
alors T suit une loi de Student à ν = n − 2 ddl.

On peut donc calculer un intervalle de confiance d’ordre 1 − α pour la pente:

    $$IC=[b-t_{1-\alpha/2}s_b, b + t_{1-\alpha/2}s_b]$$

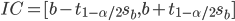
La façon de calculer cet intervalle de confiance à la main et de l’illustrer par des simulations étant extrêmement proche des méthodes que nous avons utilisées pour la pente, je vous en fais grâce… (et je vous demande donc de me croire sur parole quant à la formule analytique…). Par ailleurs, nous avons déjà évoqué la fonction confint qui permet de calculer cet intervalle de confiance sous R.

Représentation des incertitudes sur le graphe

Voici comment l’on pourrait représenter graphiquement les intervalles de confiance autour de la pente et de l’ordonnée à l’origine du modèle de régression:

layout(1:2)
plot(X,Y, main="incertitude sur la pente")
abline(reg$coeff, lwd=2, col="red")
IC_a=confint(reg)[2,]
abline(b_est,IC_a[1], col="blue")
abline(b_est,IC_a[2], col="blue")

plot(X,Y, main="incertitude sur l'ordonnée à l'origine")
abline(reg$coeff, lwd=2, col="red")
IC_b=confint(reg)[1,]
abline(IC_b[1],a_est, col="blue")
abline(IC_b[2],a_est, col="blue")

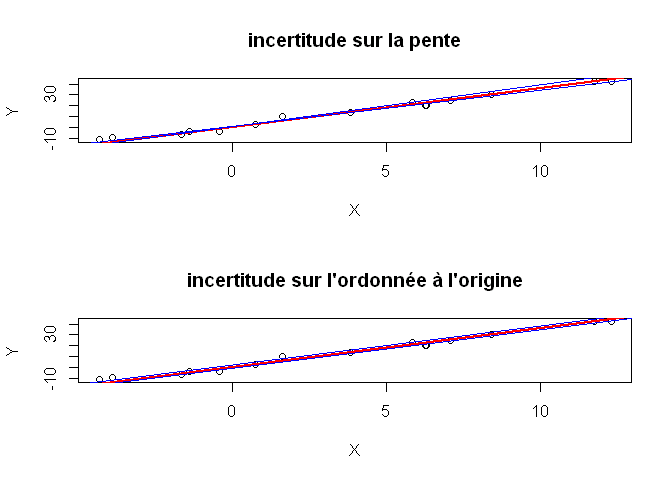
On est donc en mesure de représenter l’incertitude sur a (sous réserve que l’estimation de b soit correcte), et l’incertitude sur b (sous réserve que l’estimation de a soit correcte.

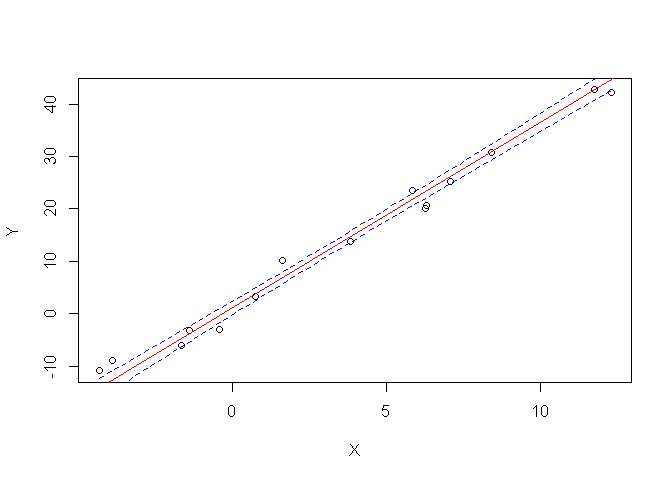
Mais, me direz-vous, comment combiner ces deux incertitudes pour représenter l’incertitude sur l’emplacement de la droite de régression, dans son ensemble?

Eh bien, on ne peut pas les combiner « directement »: il s’agit en fait d’un autre résultat analytique (eh oui!), puisqu’on cherche à estimer un intervalle de confiance non pas autour de la pente a, ou de l’ordonnée à l’origine b, mais un autour d’un point de la droite Y = aX + b

Pour consulter et comprendre le résultat analytique, vous pouvez par exemple consulter ce document issu des cours de statistiques de l’école des Mines de Nancy.

En pratique, voici la manière de calculer cet intervalle de confiance en utilisant les fonctions disponibles sous R:

plot(X,Y)
abline(reg,col="red")
newX=seq(from=min(X), to=max(X), length.out=100)
prd<-predict(reg,newdata=data.frame(X=newX),interval = c("confidence"), 
level = 0.90,type="response")
lines(newX,prd[,2],col="blue",lty=2)
lines(newX,prd[,3],col="blue",lty=2)