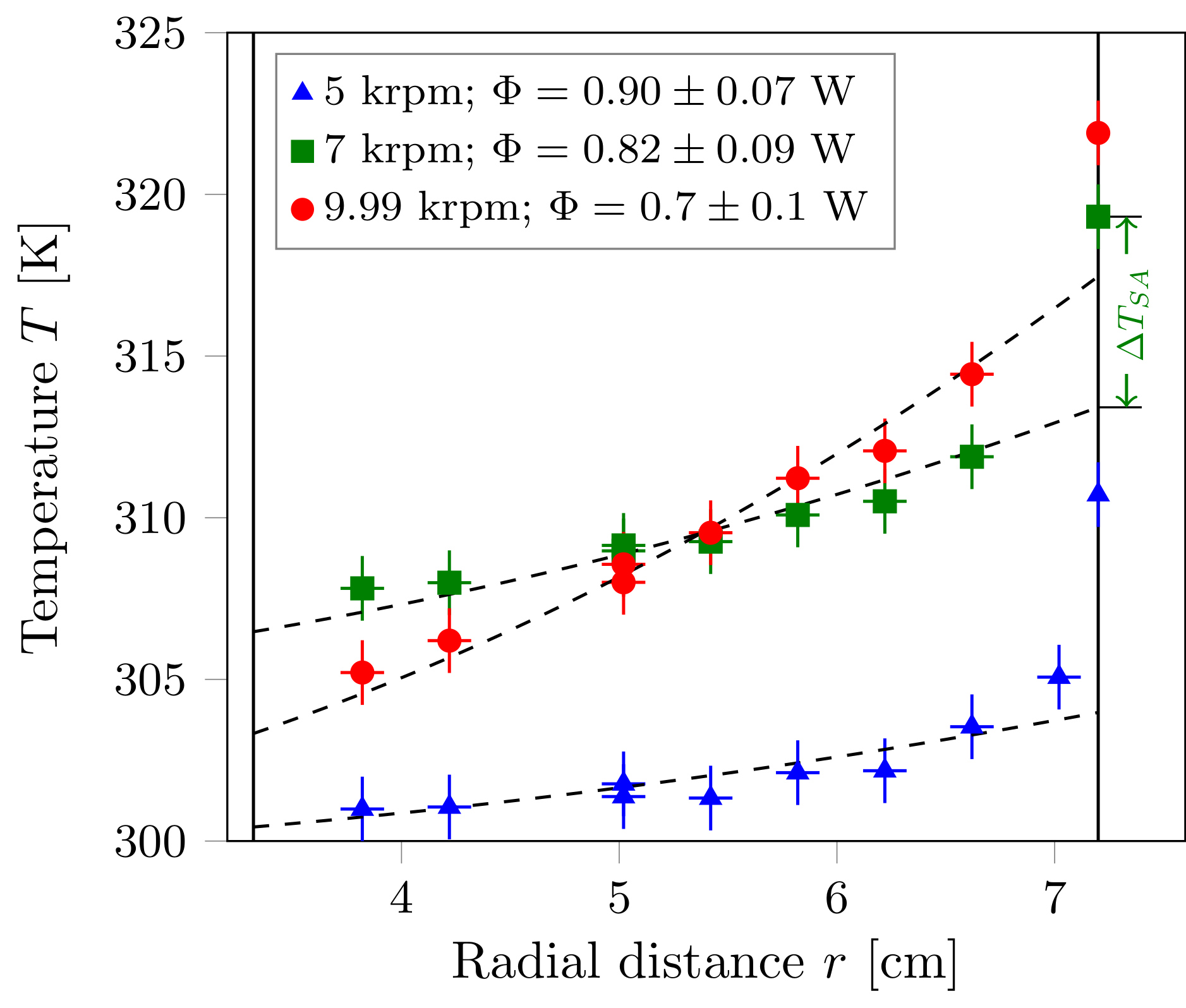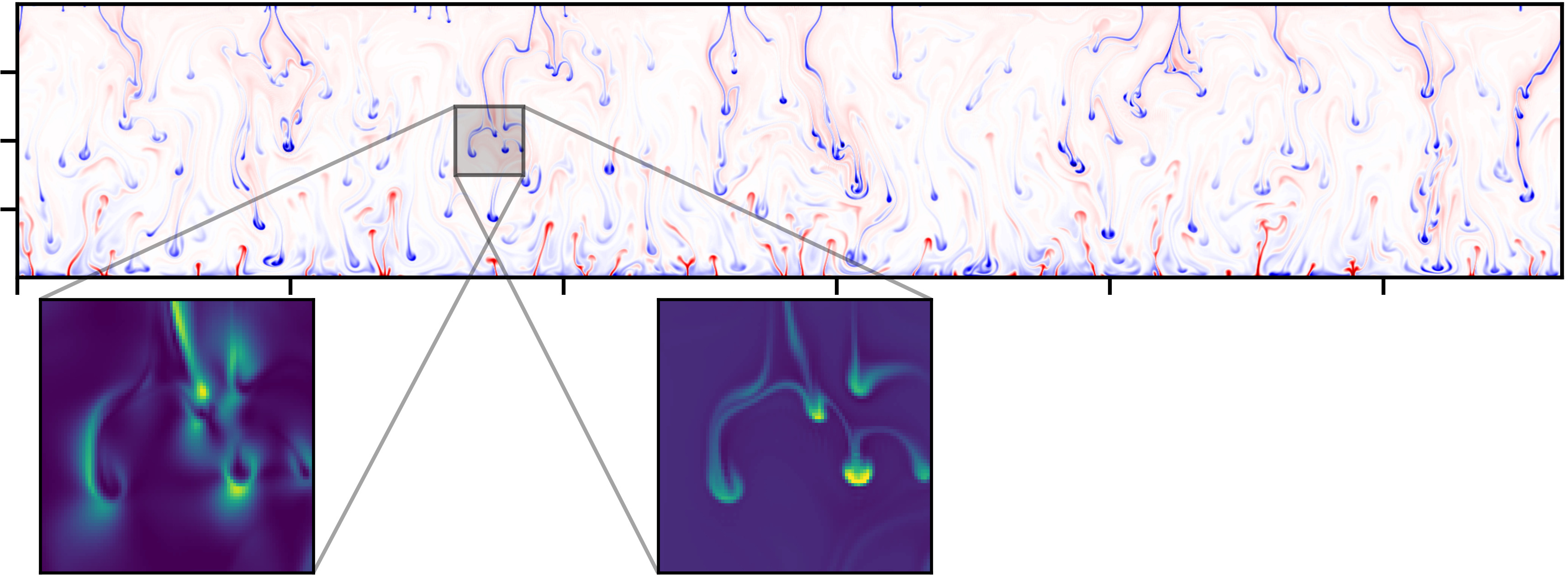
Different aspects are investigated. First, the choice of an equation of state can have an impact on convection. We have been considering the ideal gas equation of state (for atmospheres) and an equation due to Murnaghan for condensed matter (mantle, core). We have also considered a speculative equation of state with a nearly constant density: the idea is to avoid non-Oberbeck Boussinesq effects while retaining characteristic features of compressible convection such as an adiabatic temperature gradient. We used a home-made numerical model and Dedalus to run the governing equations and anelastic approximations. We analyzed the influence of compressibility on the heat flux. Our efforts were mostly devoted to understand the profile of dissipation and the total amount of dissipation. Convection experiments in a centrifuge have been performed with xenon gas. A significant adiabatic gradient was measured in a moderate compressible regime.

Whenever a phase transition takes place, the boundary between the phases has peculiar mechanical and thermal properties. We have been particularly interested in cases with a fast-dynamic phase next to a slow-dynamics phase. This happens mostly at solid-liquid interfaces (inner/outer core, water/ice, magma ocean/solid mantle). The permeability of the interface depends on thermal properties of the materials and on the intensity of the dynamics of the fast phase. Permeability can be expressed as a single dimensionless parameter.
We have also studied locally the structure of crystallization of a mushy zone when the level of gravity was changed from usual gravity to one thousand g.
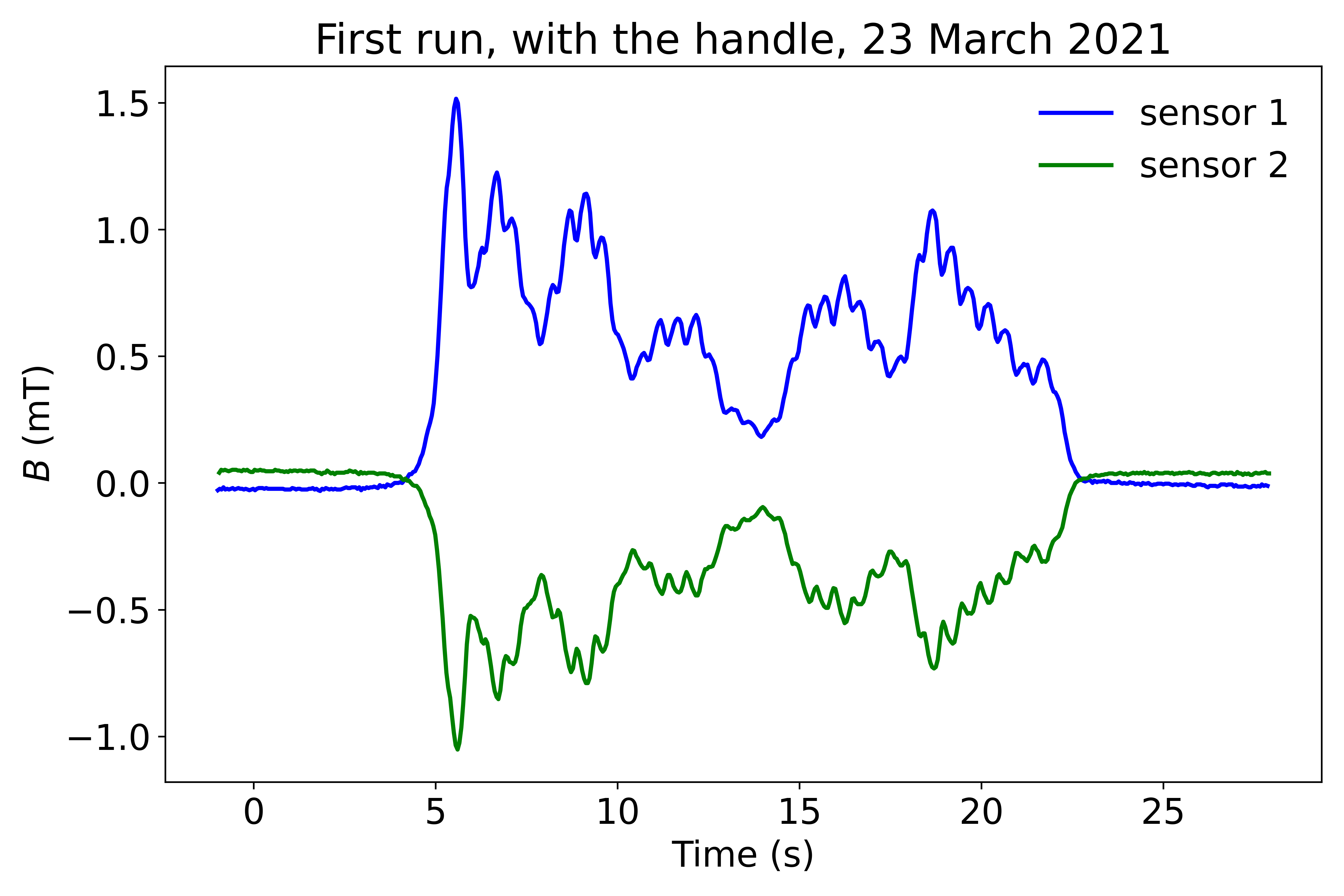
Theoretical dynamos have been considered in cartesian or cylindrical geometries with an anisotropic electrical conductivity. Solutions have been obtained analytically: the magnetic Reynolds number is a simple function of the dynamo growth rate. With analytical expressions, it is easier to derive the general properties of the dynamos. We have actually built a dynamo corresponding to this model of anisotropic conductivity. This is a solid (copper) dynamo, with a rotor in a stator, and the dynamo threshold can be obtained from human power (about 230 Watt).