Historical perspective
This term of 'compressible convection' is rather odd because pressure had its full role when the equations of dynamics were first derived. Following Navier and Stokes, the Navier-Stokes equation was first written in 1823 and finally in its present form it 1845. With density obeying an equation of state (the ideal gas law for instance), the weight of a fluid particle becomes a function of pressure and temperature. With an energy equation, the system of mass conservation, Navier-Stokes and energy equation constitutes a well-defined problem.However, the system of equations does not look very friendly, and both Oberbeck (1879) then Boussinesq (1903) came up with a radical simplification, basically considering density as uniform except when it is multiplied by gravity where it is approximated as a linear function of temperature only. This was the beginning of 'non-compressible convection', with the big success of Rayleigh obtaining the linear stability threshold of convection in 1916 for a fluid heated from below between two horizontal plates.
Since then, Boussinesq convection has been considered as 'normal convection', and the full set of equations as 'compressible convection'. But, concerning the interior of planets and stars, the compressible nature of convection cannot be ignored. Hydrostatic pressure is the main cause of density change (even for a 'solid' mantle). Associated with hydrostatic pressure, adiabatic compression and decompression leads to a temperature gradient (the 'adiabatic' gradient) that is missing in a Boussinesq model.
Modelling contributions
In this context, there have been investigations on the differences between Boussinesq and compressible convection. With Yanick Ricard, we have shown that independent assumptions should not be made on thermophysical quantities: for instance, assuming that the expansion coefficient is small (compared to 1/T) is not compatible with a constant value of the heat capacity (at constant pressure). Otherwise inconsistent expressions for viscous dissipation are obtained (see this paper in JFM). We have also investigated the linear stability of the Bénard configuration and obtained approximate results for any possible equation of state (see this paper in JFM).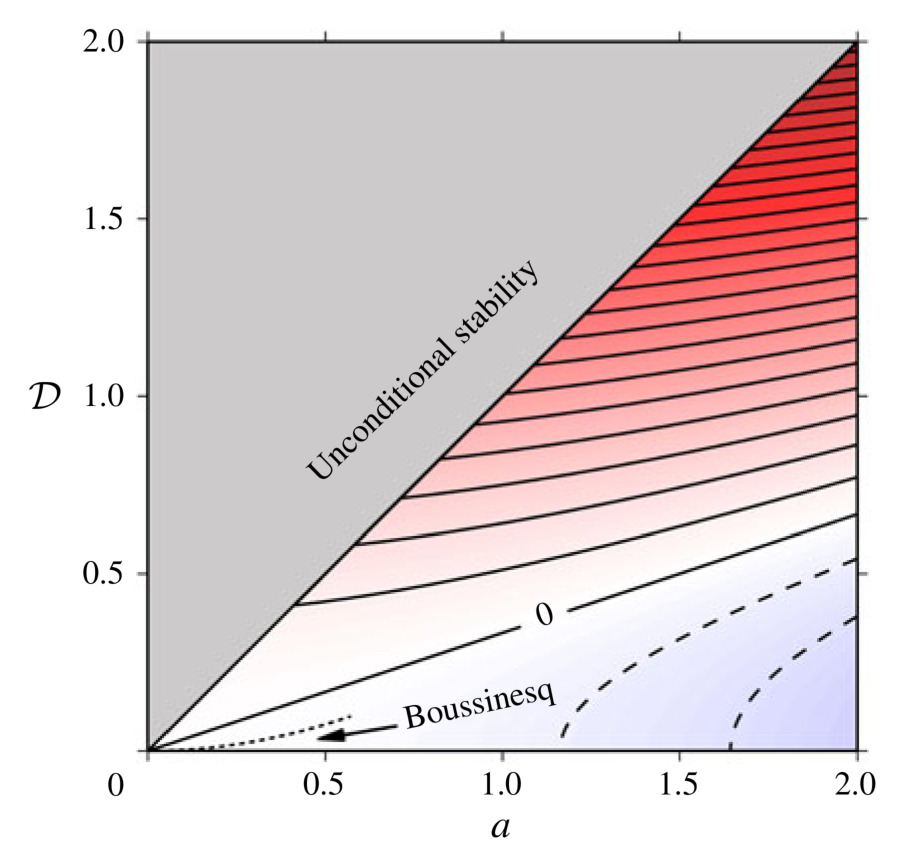
With Jezabel Curbelo and Lucia Duarte, starting with their post-doctoral positions in Lyon, and colleagues from may lab (Stéphane Labrosse, Yanick Ricard and Fabien Dubuffet), we have investigated numerically compressible convection and anelastic models, intermediate between Boussinesq and complete equations. Those anelastic models (and other sound-proof models) remove sound-waves while retaining other compressible effects, or at least this is the objective... We found that a small value for the dissipation parameter was enough to ensure good convergence of anelastic models (see this paper in JFM).
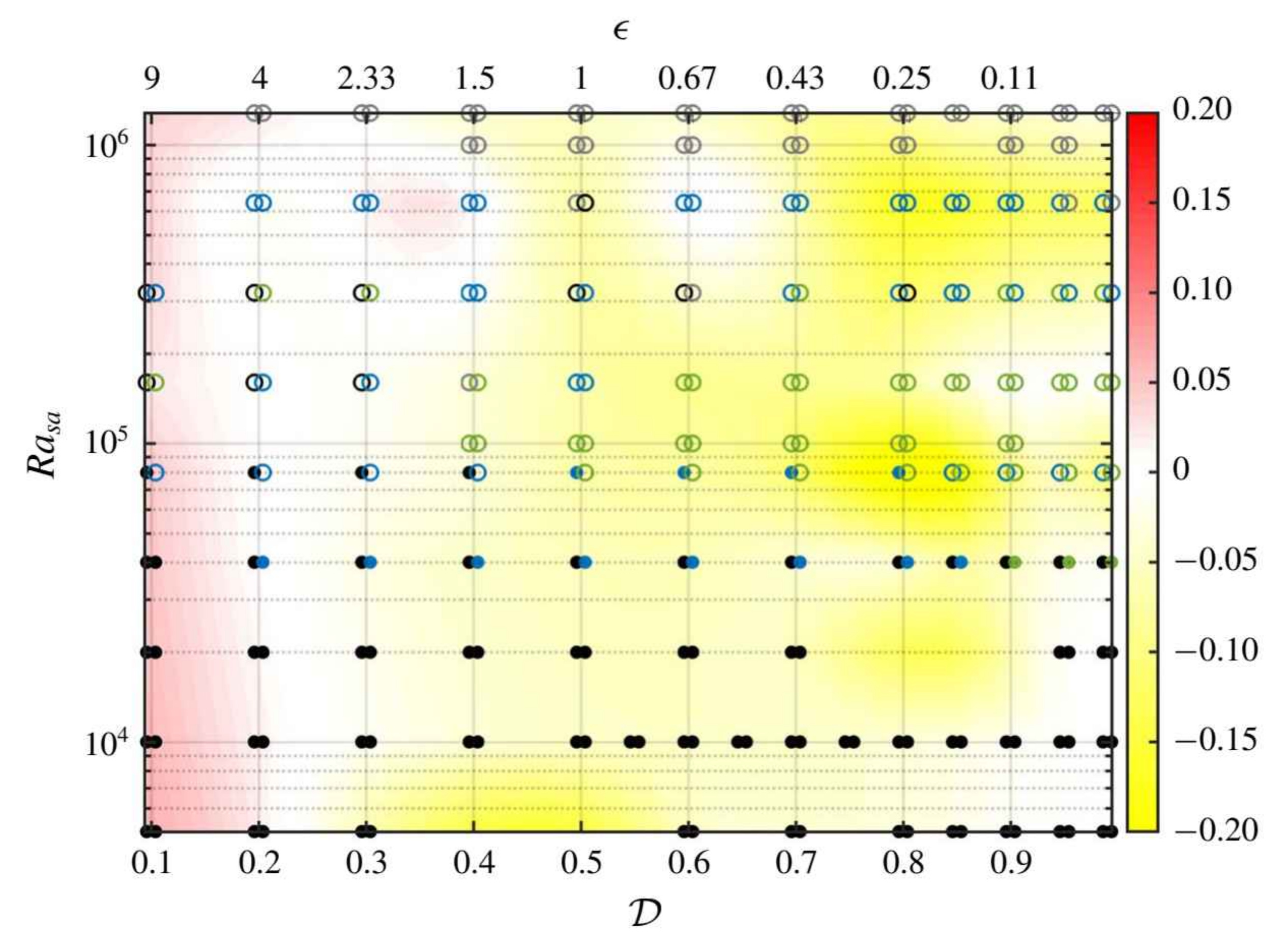
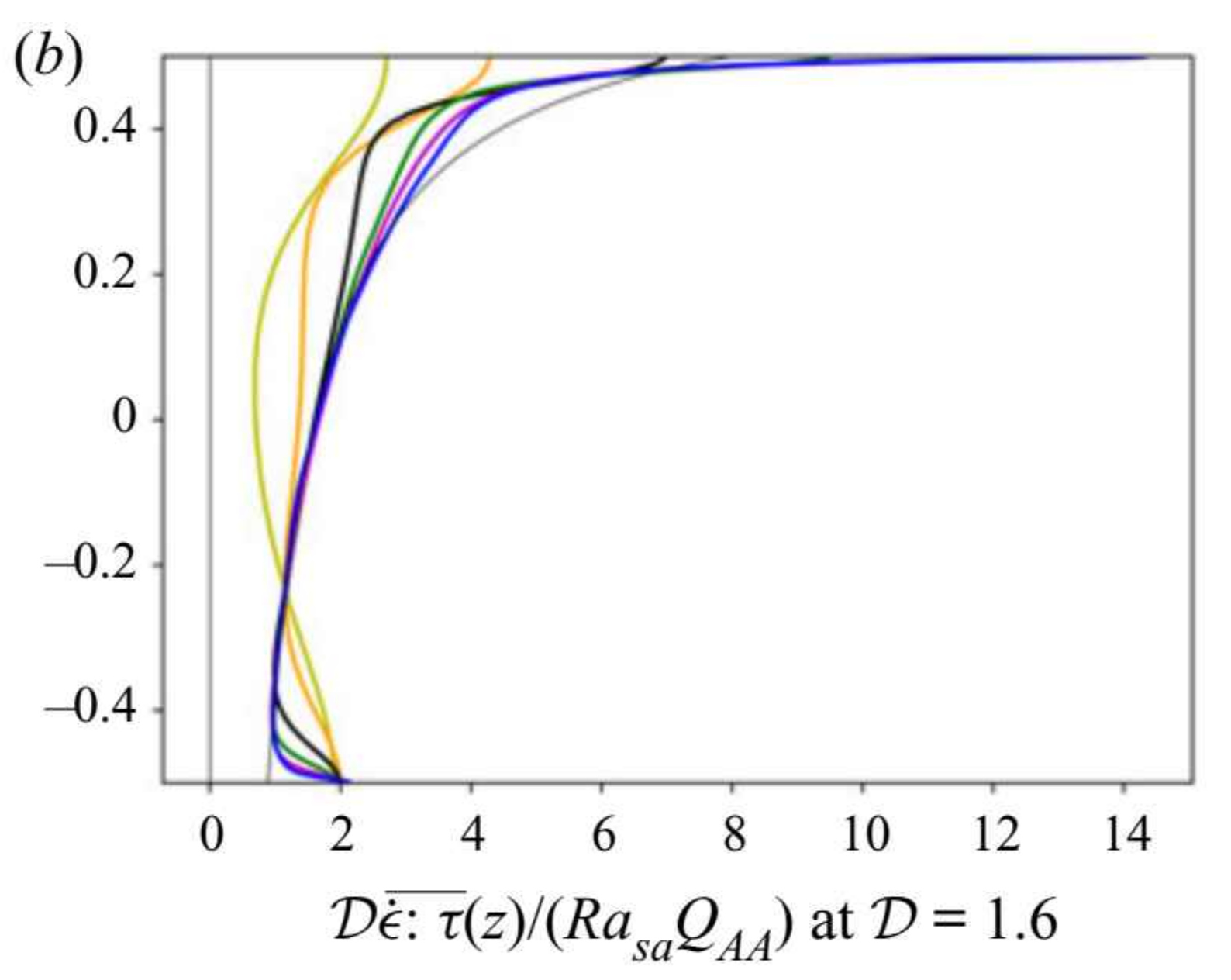
With Jezabel Curbelo, Stéphane Labrosse, Fabien Dubuffet and Yanick Ricard, we used Dedalus to study compressible convection using a particular equation of state minimizing density contrasts. We observed a convergence of the vertical profile of viscous dissipation toward a well-defined limit where viscous dissipation balances locally a function of the entropy flux, see this paper in JFM. A similar trend has been found with a Murnaghan equation of states (see this paper in GJI).
Experimental Compressible Convection
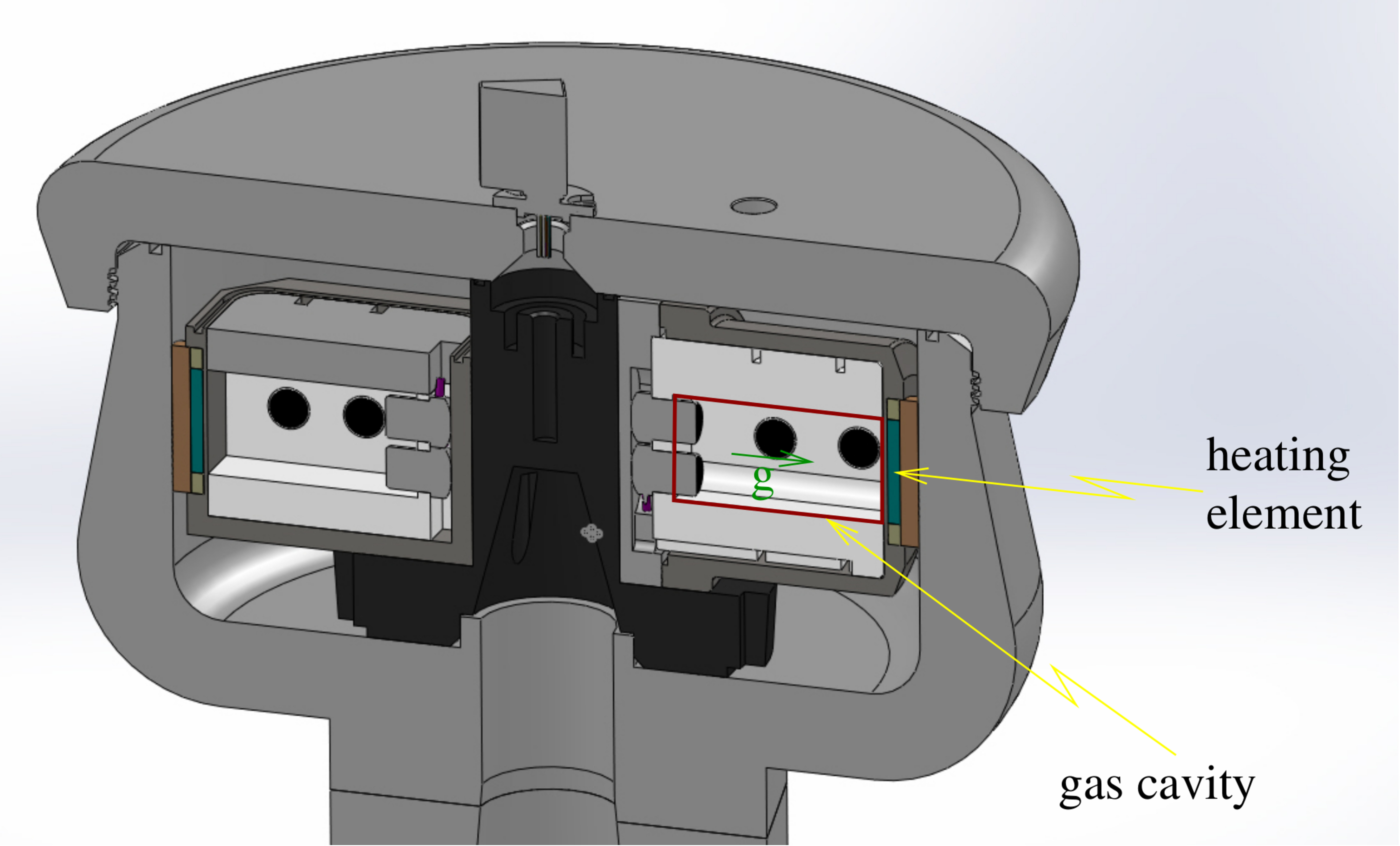
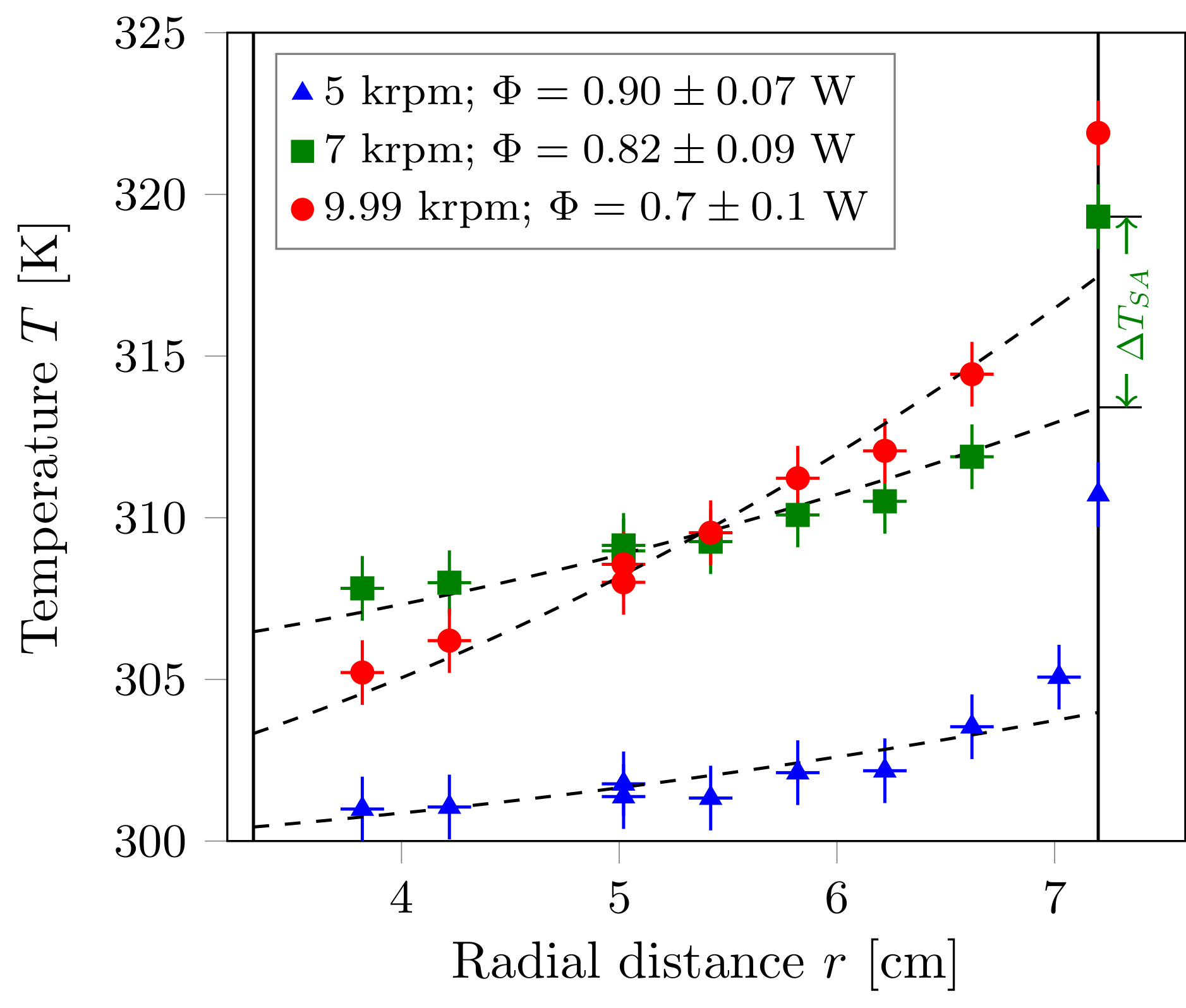
During the thesis of Yoann Corre and Rémi Menaut, we have designed and built an experimental device of convection placed in a rotor centrifuge. In order to maximize the adiabatic gradient, we have filled the cavity with xenon gas. Convection with some degree of compressibility has been studied. Under 7000 g, we have measured an adiabatic gradient of 15 degrees over a distance of 4 cm (see this paper in PRF).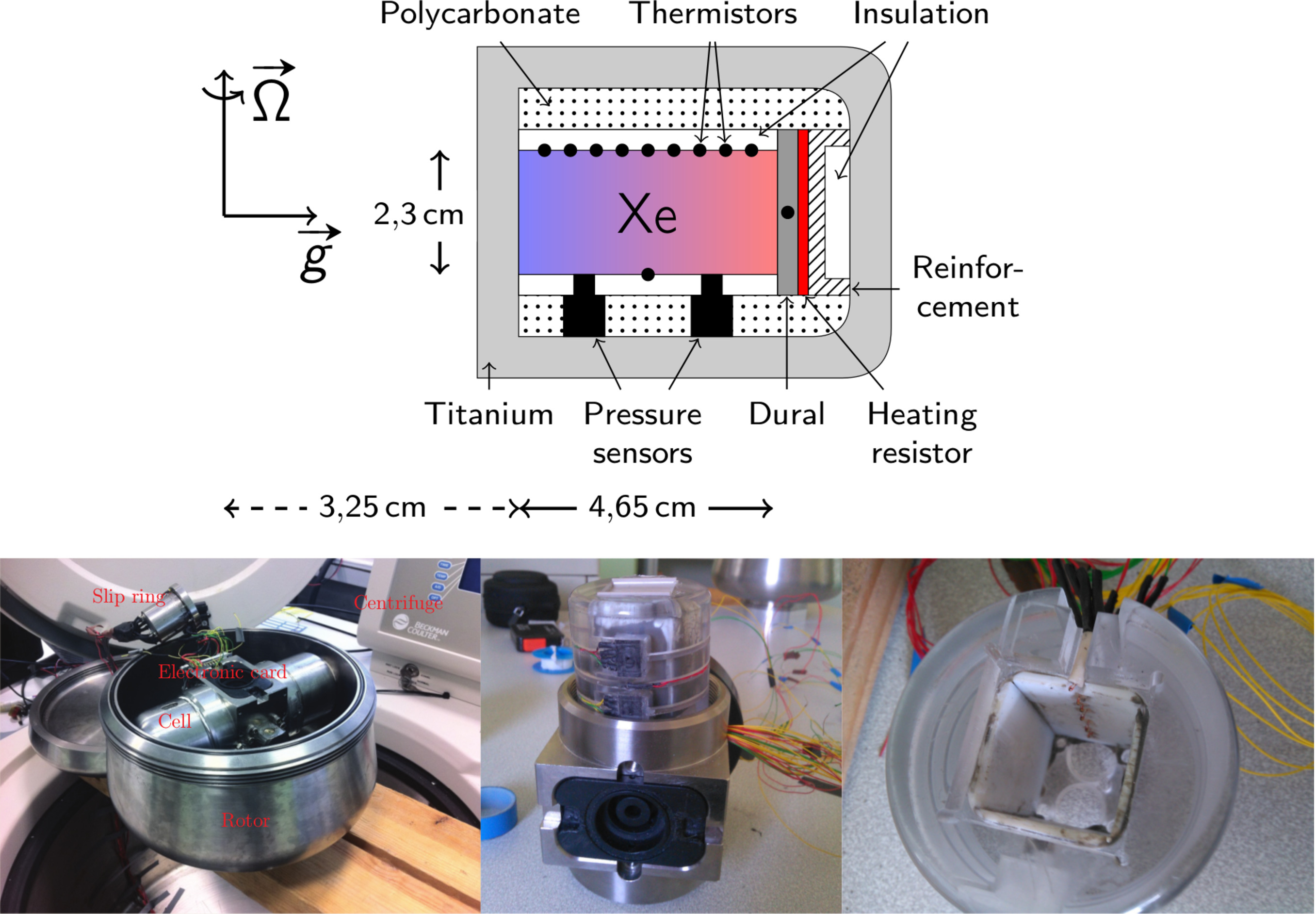

Adrar, Mauritania
