Welcome
I’m an Inria researcher in the AriC team, which is part of the LIP lab in ENS Lyon. My field of research is computer algebra. It is the study of effective mathematics and their complexity: how much mathematics can be done by a computer, and how fast? In this area, I am mostly interested in applications to classical analysis (asymptotics, special functions) and combinatorics. See the menus “Software” and “Publications” for more information.
Book
In 2017, we published a book version of the notes of the course on efficient algorithms for computer algebra we have been giving for more than 10 years. Click on the cover to reach a page where you can download it for free or order an inexpensive paper version.
Recent Work
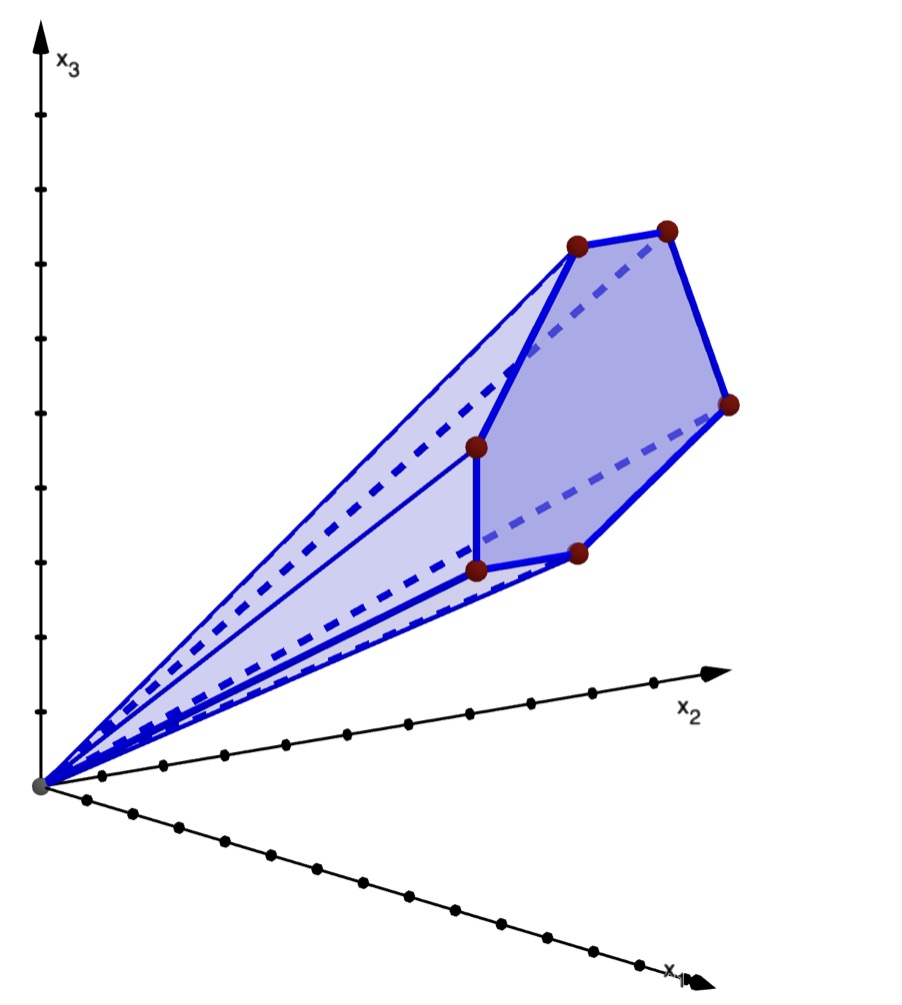
The cone in the picture contains all vectors $(u_n,u_{n+1},u_{n+2})^t$ for \(n\ge N\) where \(N\) is known, where \((u_n)_{n\in\mathbb N}\) is a sequence defined by a linear recurrence of order 2 and with polynomial coefficients. This cone is a means to prove that the sequence is positive: one checks the first values up to \(n=N\) and then one proves that the sequence does not leave the cone. In this work, we show that this approach applies to solutions of linear recurrences with polynomial coefficients of arbitrary order, provided they are of Poincaré type and with a unique simple dominant eigenvalue. In this situation, deciding positivity reduces to deciding the genericity of initial conditions in a precisely defined way. We give an algorithm that produces a certificate of positivity that is a data-structure for a proof by induction. This induction works by showing that a cone computed from the recurrence is contracted by the iteration.
A. Ibrahim and B. Salvy, “Positivity certificates for linear recurrences,” in Proceedings of the 2024 Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), 2024, pp. 982–994. Contains an earlier algorithm for this problem that is not as efficient as the new one.
Getting a good numerical code for the computation of the hypothenuse is not as simple as it looks. Compromises have to be made between efficiency, avoiding overflows and underflows and getting a small relative round-off error. We focus on the last issue and provide tools to help automate the error analysis of algorithms that evaluate simple functions over the floating-point numbers. The aim is to obtain tight relative error bounds for these algorithms, expressed as a function of the unit round-off. Due to the discrete nature of the set of floating-point numbers, the largest errors are often intrinsically “arithmetic” in the sense that their appearance may depend on specific bit patterns in the binary representations of intermediate variables, which may be present only for some precisions. We focus on generic (i.e., parameterized by the precision) and analytic over-estimations that still capture the correlations between the errors made at each step of the algorithms. Using methods from computer algebra, which we adapt to the particular structure of the polynomial systems that encode the errors, we obtain bounds with a linear term in the unit round-off that is sharp in many cases. An explicit quadratic bound is given, rather than the $O()$-estimate that is more common in this area. This is particularly important when using low precision formats, which are increasingly common in modern processors. Using this approach, we compare five algorithms for computing the hypotenuse function, ranging from elementary to quite challenging.
See also the BoundRoundingError package.
The picture on the right, from the cover of a book by Kenneth Chan on ‘‘Spacecraft collision probability’’, illustrates the quantity of debris orbiting around Earth and the importance of predicting collisions. Among the available risk indicators, we focus on computing the instantaneous probability of collision, which can be modeled as the integral of a three-dimensional Gaussian probability density function over a Euclidean ball. We propose an efficient and accurate method for evaluating this integral. It is based on the combination of two complementary strategies. For the first one, convergent series and numerical error bounds are computed. These bounds provide a tradeoff between the accuracy needed and the number of terms to compute. The second one, using divergent series, approximates the value of the integral with a good accuracy in most cases with only a few terms computed. Based on those two methods, a hybrid algorithm is tested on cases borrowed from the literature and compared against existing methods. Several numerical results and comparisons confirm both the efficiency and robustness of our approach.
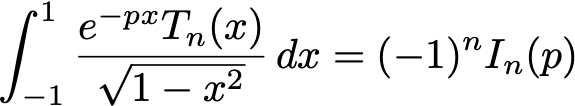Definite sums and integrals involving special functions and sequences can be
dealt with automatically with a computer algebra technique called
creative telescoping. Classical algorithms rely on the computation
of an intermediate object called a certificate, whose size can be
large and whose computation may be expensive. It turns out that for a
large class of sums and integrals, this part of the computation can be avoided,
speeding up the whole process.
See also the CreativeTelescoping package.
A power series being given as the solution of a linear differential equation with appropriate initial conditions, minimization consists in finding a non-trivial linear differential equation of minimal order having this power series as a solution. This problem exists in both homogeneous and inhomogeneous variants; it is distinct from, but related to, the classical problem of factorization of differential operators. Recently, minimization has found applications in Transcendental Number Theory, more specifically in the computation of non-zero algebraic points where Siegel’s \(E\)-functions take algebraic values. We present algorithms for these questions and discuss implementation and experiments.
We have designed a new algorithm (of the Las Vegas type) for the composition of two polynomials modulo a third one, over an arbitrary field. When the degrees of these polynomials are bounded by \(n\), the algorithm uses \(O(n^{1.43})\) field operations, breaking through the \(3/2\) barrier in the exponent for the first time. The previous fastest algebraic algorithms, due to Brent and Kung in 1978, require \(O(n^{1.63})\) field operations in general, and \({n^{3/2+o(1)}}\) field operations in the particular case of power series over a field of large enough characteristic. If using cubic-time matrix multiplication, the new algorithm runs in \({n^{5/3+o(1)}}\) operations, while previous ones run in \(O(n^2)\) operations.
Our approach relies on the computation of a matrix of algebraic relations that is typically of small size. Randomization is used to reduce arbitrary input to this favorable situation.
Many families of hypergeometric series (but not all) share properties that are well-known for classical orthogonal polynomials. We consider six general families of hypergeometric series in a variable \(x\), indexed by an integer \(n\) and with an arbitrary number of parameters. For each of them, we give explicit factorizations of recurrence operators in \(n\) that their derivative with respect to \(x\) and their product by \(x\) satisfy.
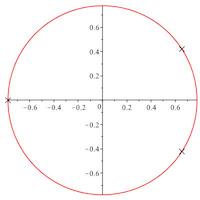
The three complex roots of the polynomial \(17x^3-9x^2-7x+8\), depicted on the picture, lie on two different circles, at distance smaller than 0.000015 and thus indistinguishable on the picture. Bounds are known for the distance between absolute values of roots of polynomials with integer coefficients. We improve the known bounds and run extensive experiments in small degrees in order to assert the quality of these bounds, that seem to be quite pessimistic.
Analytic combinatorics in several variables aims at finding the asymptotic behavior of sequences of diagonal coefficients of multivariate analytic functions. The starting point of the computation is the determination of the set of minimal critical points of the set of singularities. These are points where this set comes closest to the origin. In the case of rational functions with nonnegative coefficients, this can be achieved efficiently. In general, the situation can still be handled, with a higher computational complexity.
Linear differential operators behave like polynomials for many operations, but not for factorization. In particular, the degrees of the coefficients of factors of linear differential operators can be extremely large. It is however possible to give bounds on these degrees that depend only on the order, degree of the coefficients and size of the integer coefficients of the operators.
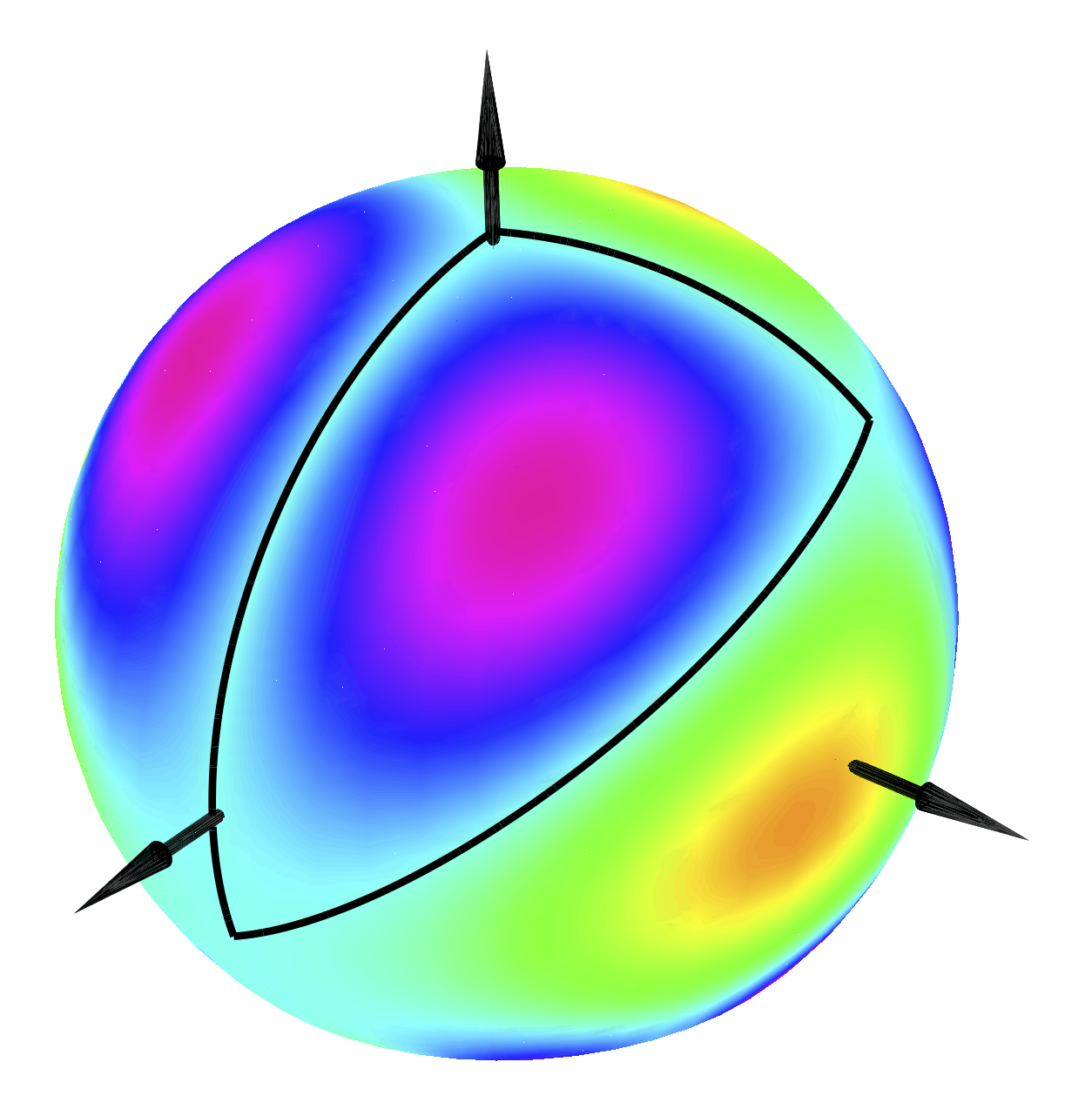
This picture of the eigenfunction for the fundamental eigenvalue of the Laplacian on the spherical triangle with angles \( (2\pi/3,\pi/3,\pi/2) \) originally comes from a problem in the study of random walks in \( \mathbb{N}^3 \) using a restricted step set. Each step set can be associated to a spherical triangle and the asymptotic behaviour of the number of walks \(e_n\) with \( n\) steps, say from \( (0,0,0)\) to itself is of the form \(C \rho^n n^\alpha\) where \(\rho\) is easy to compute from the step sets and \(\alpha \) is related to that fundamental eigenvalue. The sequence \( (e_n)_n \) cannot be solution to a linear recurrence if that exponent \(\alpha\) is not rational. This motivates the study of certified high-precision approximations to the fundamental eigenvalues of spherical triangles. We do this by a combination of the classical method of particular solutions, interval arithmetic, Taylor models and several other tools that let us obtain in particular 100 digits of the fundamental eigenvalue for the 3D Kreweras model. From there, a continued fraction expansion lets us conclude that if the corresponding exponent \(\alpha\) were rational, its denominator would be at least \(10^{51}\).
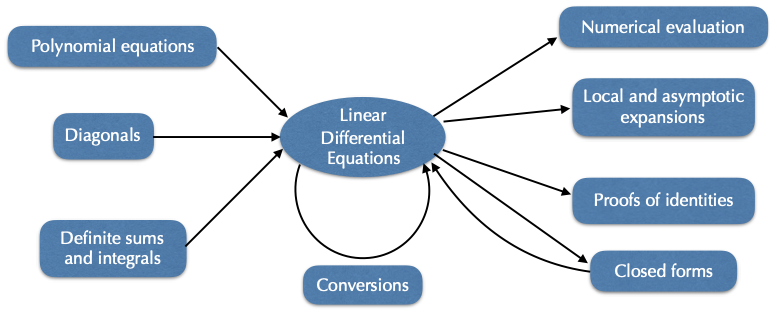A lot of information concerning solutions of linear differential equations can be computed directly from the equation. It is therefore natural to consider these equations as a data-structure, from which mathematical properties can be computed. A variety of algorithms has thus been designed in recent years that do not aim at “solving”, but at computing with this representation. Many of these results are surveyed in this article.
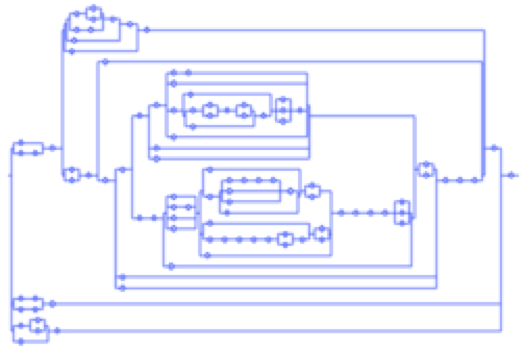
The probabilistic behaviour of many data-structures, like the series-parallel graphs in the picture, can be analysed very precisely, thanks to a set of high-level tools provided by Analytic Combinatorics, as described in the book by Flajolet and Sedgewick. In this framework, recursive combinatorial definitions lead to generating function equations from which efficient algorithms can be designed for enumeration, random generation and, to some extent, asymptotic analysis. With a focus on random generation, this tutorial given at STACS first covers the basics of Analytic Combinatorics and then describes the idea of Boltzmann sampling and its realisation. The tutorial addresses a broad TCS audience and no particular pre-knowledge on analytic combinatorics is expected.
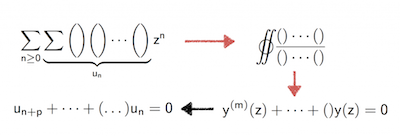
Multiple binomial sums turn out to be diagonals of rational power series. This can be made effective, leading to an integral representation from which a linear differential equation for the generating function can be derived and from there finally a linear recurrence for the sum. This is a very efficient approach that avoids the computation of a large certificate.
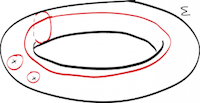
Definite integrals of rational functions in several variables provide elementary representations for a large number of special functions, or combinatorial sequences through their generating functions. These integrals satisfy linear differential equations from which a lot of information about them can be extracted easily. The computation of these integrals is a classical topic, going back at least to Émile Picard, with recent progress based on creative telescoping.
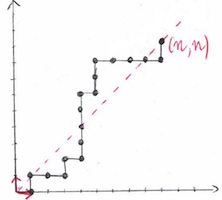
Diagonals of multivariate rational functions encode the enumeration sequences of many combinatorial sequences. In the bivariate case, these diagonals are algebraic power series and an alternative representation is by their minimal polynomial. Yet another possibility is to use a linear differential equation they satisfy. Precise estimates of the sizes of these equations and of the complexity of obtaining them can be computed, showing that the differential equation is generally a better choice.
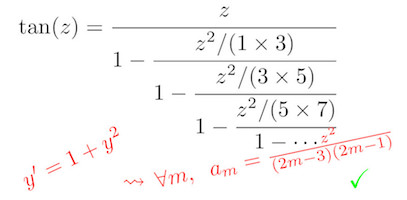
Continued fractions provide a sequence of approximations to a number or a function in the same way as series expansions or infinite products do. For a large number of special functions, these continued fractions have coefficients given by an explicit rational function of the index. To a large extent, these formulas can be discovered and proved by computer algebra.
The full collection of my recent (and not so recent) papers is here.
Address
46, allée d'Italie
69364 Lyon Cedex 07
France
email: Firstname.Lastname@inria.fr
phone: (+33) (0)4 72 72 89 01