research
string theory
String theory is a theory to describe nature at the smallest length scales. Replacing the concept of point-like elementary particles by extended strings, it describes a unification of the fundamental interactions, including the gravitational force. Consistency of string theory requires supersymmetry, a fundamental symmetry between bosons and fermions. Its presence leads to various cancellations of the divergences from which ordinary quantum field theories typically suffer. String theory furthermore predicts the existence of six extra spatial dimensions which are required for mathematical consistency of the theory. The analysis of their compactification draws on the historical work by Kaluza and Klein which attempts to unify gravity and electromagnetism by introducing a fifth dimension to Einstein's general relativity.
supergravity
At low energies and after compactification of the extra dimensions, string theory is described by so-called gauged supergravity theories. These are four-dimensional field theories combining supersymmetry, gauge symmetry and gravity. The properties of the compactified dimensions and their internal six-dimensional geometry manifest themselves in their particle spectrum, their couplings, and their symmetries. Other applications of gauged supergravities include the so-called holographic dualities between string theory on certain curved backgrounds and supersymmetric quantum field theories defined on the boundary.
exceptional geometry
Duality symmetries have been at the heart of string theory since the mid 90s with the discovery of the uniqueness of an underlying structure (M-theory) connecting the various string theories. Only recently, a manifestly duality covariant formulation of supergravity theories has emerged from related developments in mathematics and physics. Other than of conceptional interest, these so-called exceptional field theories provide a set of powerful tools in order to address some longstanding questions in supergravity theories. This is particularly relevant for the study of vacua and of consistent truncations of higher-dimensional supergravity on non-trivial backgrounds. On a more fundamental level, these applications trigger tempting questions towards a more fundamental description of supergravity and string theory.
Kaluza-Klein spectroscopy
Exceptional field theory provides systematic and efficient methods for computing Kaluza–Klein mass spectra in supergravity compactifications. Unlike traditional approaches that often rely on highly symmetric backgrounds, this
framework grants access to deformed and less symmetric compactifications that are otherwise intractable. Crucially, it applies to settings not protected by supersymmetry. The method has been applied to compute the full Kaluza–Klein spectrum around vacua with little or no symmetry, uncovering universal mass formulae, and resolving several long-standing questions in supergravity. It has enabled the identification of perturbatively stable non-supersymmetric AdS vacua, and provided the first holographic evidence for nonsupersymmetric conformal manifolds.
Henning Samtleben
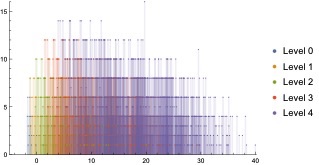
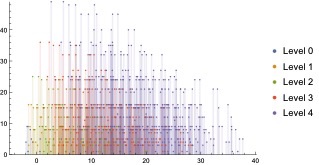
Perturbatively stable scalar mass spectra around non-supersymmetry AdS4 vacua of massive IIA supergravity. Work with A. Guarino and E. Malek.