Il y a maintenant quelques mois, je suis tombée sur ce tweet de thinkR (toujours sur les bons coups!) qui m’a fait découvrir le génial package infer. En découvrant la présentation de Chester Ismay (pas tellement la première partie qui parle de « tidy data » mais surtout la deuxième, à partir de la diapo… 118 -!!-) j’ai réalisé que ce package allait probablement changer ma vie d’enseignante/formatrice (occasionnelle) ayant à expliquer les tests statistiques. Et après, j’ai réalisé qu’en fait, il pouvait également me faciliter ma vie d’analyste de données (parce que la simplicité, ce n’est pas que pour les étudiants, moi aussi j’aime bien!).

infer: pour quoi faire?

Le package infer permet, dans un premier lieu, d’expliciter et illustrer le raisonnement sous-jacent aux tests statistiques (comme le t-test ou le test du χ²). Il permet en outre de s’abstraire (dans une certaine mesure) des problèmes de non-respect des hypothèses de ces tests en permettant de calculer la distribution des statistiques de test via des permutations plutôt qu’en s’appuyant sur les distributions théoriques des statistiques sous hypothèse de normalité, d’homoscedasticité, ou de taille d’échantillon ou effectifs « suffisants ».

De fait, je me suis empressée d’intégrer quelques exemples d’utilisation du package infer à mon Grimoire Stat puis à m’en servir dans le cadre de ma (mini-)formation aux tests stats. Je ne souhaite pas ici rentrer dans le même niveau de détail que dans les deux documents sus-mentionnés, ou m’adresser au même public. Ce billet de blog s’adresse à ceux qui ont déjà compris la logique des tests statistiques, mais qui recherchent des outils pour faciliter leur enseignement… Aussi, si vous souhaitez comprendre les tests statistiques, je vous invite à consulter le grimoire Stat (version longue) ou la formation (version synthétique)…

En effet, si vous êtes amenés à enseigner les tests statistiques, le package infer est particulièrement intéressant dans le cas où vous adoptez le parti pris de l’initiation à R par le tidyverse. En effet, infer répond aux mêmes logiques de syntaxe et de programmation (avec des commandes « pipables » par exemple). Il est aussi également particulièrement intéressant si vous souhaitez enseigner les statistiques à des gens qui ne savent pas ou ne sont pas encore à l’aise pour réaliser des simulations « à la main ».

En effet, le package prend en charge la réalisation de nombreuses permutations des données qui permettent de calculer la distribution empirique d’une statistique sous hypothèse nulle (et donc le calcul d’une p-value) même si les hypothèses permettant de déduire la distribution théorique de la statistique ne sont pas réunies.

Les créateurs du package illustrent cette idée de la manière suivante:

Par le passé, j’étais toujours un peu embêtée en enseignant les tests statistiques quand j’en venais à la partie vérification des hypothèses de normalité/homoscedasticité/échantillons de grande taille/effectifs élevés. En effet, la robustesse des méthodes d’inférence est telle qu’on peut souvent s’y fier quand bien-même la vérification des hypothèses serait douteuse (qu’est-ce qu’un échantillon de grande taille? quand est-ce que l’écart aux hypothèses est tel que la taille d’échantillon ne suffit plus à le compenser?). J’avais d’ailleurs fait un billet de blog sur ce sujet (intitulé « Non-respect des hypothèses du modèle linéaire: c’est grave, docteur? ») qui montrait que l’on pouvait se fournir quelques repères pour répondre à ces questions en réalisant quelques simulations. Néanmoins, recourir à des simulations pour évaluer si l’on était en mesure d’utiliser un test paramétrique classique signifiait un effort non-négligeable pour modéliser le problème et réaliser les simulations en question. C’est maintenant beaucoup plus simple à l’aide du package infer, en tout cas pour les tests pris en charge par le package!

En pratique, infer réalise l’ensemble des opérations nécessaires à ce processus à travers de fonctions (ou verbes) dont l’articulation est illustrée ci-dessus (illustration issue de ce diaporama, déjà mentionné)

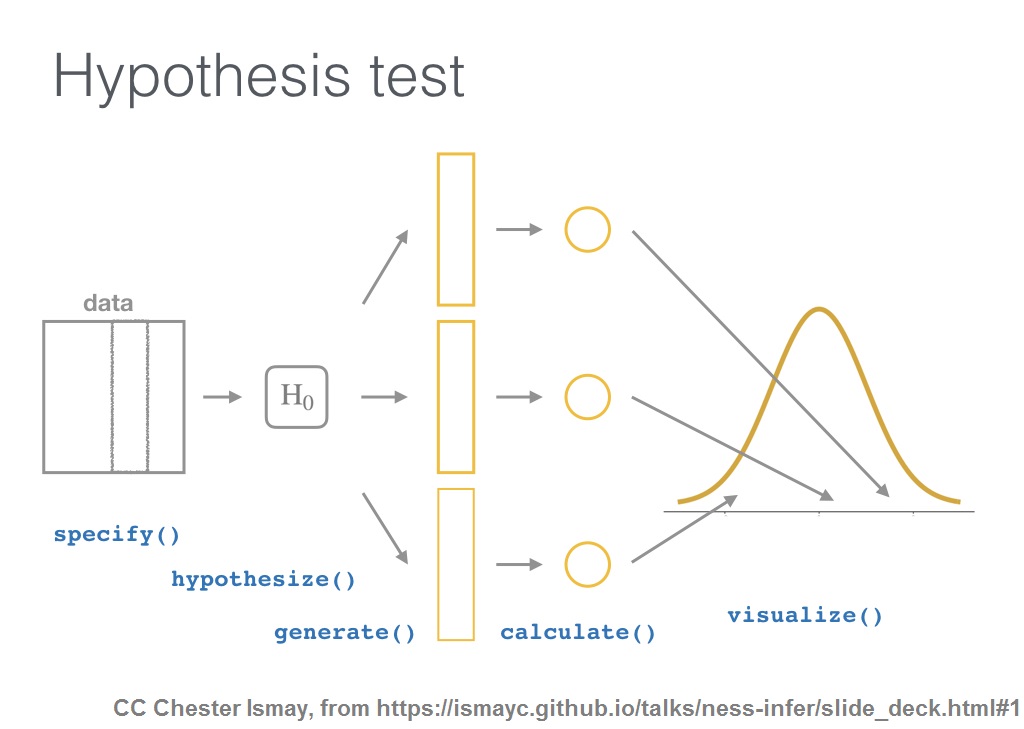
Je montre dans la suite de ce document 3 exemples d’utilisation du package:

• un exemple de t-test (basé sur la distribution théorique de la statistique T sous hypothèse d’indépendance)
• un exemple de test du χ² (basé sur la distribution théorique de la statistique du χ² sous hypothèse d’indépendance)
• un exemple de test du χ² (basé sur une distribution de la statistique du χ² sous hypothèse d’indépendance calculée par des permutations du jeu de données)

Exemple 1: t-test

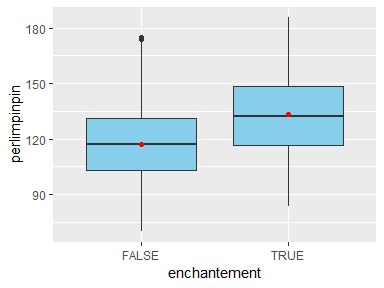
Je vais ici utiliser les données broceliande de mon grimoire Stat pour illustrer la réalisation d’un t-test à l’aide du package infer. Imaginons par exemple que je souhaite tester l’effet de l’enchantement sur la quantité de poudre de perlimpinpin produite par mes arbres:

datasets_path="http://perso.ens-lyon.fr/lise.vaudor/grimoireStat/datasets/"
broceliande=readr::read_delim(paste0(datasets_path,'broceliande.csv'),
                              delim=';')
ggplot(broceliande, aes(x=enchantement, y=perlimpinpin))+
  geom_boxplot(fill="skyblue")+
  geom_point(data= broceliande %>% 
               group_by(enchantement) %>% 
               summarise(perlimpinpin=mean(perlimpinpin)),
             color="red")

La fonction de infer pour réaliser le t-test est t_test():

montest1 <- broceliande %>% 
  t_test(perlimpinpin ~ enchantement,
         order=c(TRUE, FALSE))

t_obs=montest1 %>% 
  select(statistic)

L’argument order me permet de dire dans quel sens j’effectue la comparaison de moyenne (ici je considère la moyenne des arbres enchantés (enchantement est TRUE) moins la moyenne des arbres non-enchantés (enchantement est FALSE).

Je peux décomposer le processus et produire une visualisation montrant l’emplacement de la statistique observée par rapport à la distribution théorique attendue sous hypothèse d’indépendance via les verbes du package:

broceliande %>%
  specify(perlimpinpin ~ enchantement) %>%
  hypothesize(null = 'independence') %>% 
  calculate(stat = 't') %>% 
  visualize(method = 'theoretical',
            obs_stat=t_obs,
            direction = 'two_sided')

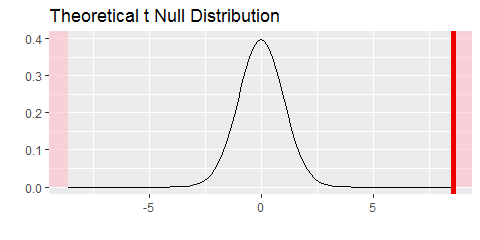
Dans ce cas, je me contente de considérer la distribution théorique sous hypothèse nulle car les conditions permettant de supposer que la statistique T suit cette distribution sont respectées. De ce fait, je ne me sers pas du verbe generate()… Je vous montrerai comment utiliser ce verbe dans mon troisième exemple.

Exemple 2: test du Chi-2

Intéressons-nous maintenant au jeu de données fantaisie, et au lien entre sexe et activite.

fantaisie=readr::read_delim(paste0(datasets_path,'chateauxEtBoulots.csv'),
                            delim=';')

fantaisie %>% 
  janitor::tabyl(sexe,activite)

##      sexe chevalerie enchantements magie_noire royaute
##   feminin          0            13          14       9
##  masculin         18             3           8       7

Le package janitor permet de transformer ce tableau d’effectifs pour afficher à la fois les pourcentages (ici par colonne) et les effectifs, ce qui en facilite l’interprétation.

fantaisie %>% 
  janitor::tabyl(sexe,activite) %>% 
  janitor::adorn_percentages("col") %>% 
  janitor::adorn_pct_formatting(digits=2) %>% 
  janitor::adorn_ns()

##      sexe   chevalerie enchantements magie_noire    royaute
##   feminin   0.00%  (0)   81.25% (13) 63.64% (14) 56.25% (9)
##  masculin 100.00% (18)   18.75%  (3) 36.36%  (8) 43.75% (7)

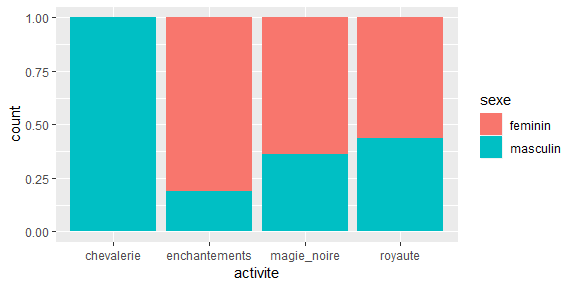
ggplot(fantaisie,aes(x=activite))+
  geom_bar(aes(fill=sexe),position="fill")

La fonction de infer pour réaliser un test du χ² est chisq_test()

montest2 <- fantaisie %>% 
  chisq_test(formula=activite~sexe)
print(montest2)

## # A tibble: 1 x 3
##   statistic chisq_df    p_value
##       <dbl>    <int>      <dbl>
## 1      26.1        3 0.00000893

chi_obs=montest2 %>%
  pull(statistic)

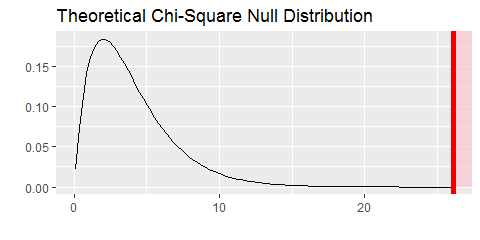
Pour visualiser la distribution théorique de la statistique et l’emplacement de la statistique observée, la logique est exactement la même que dans le cas du t-test (sauf qu’on adapte la nature de la statistique calculée!):

fantaisie %>%
  specify(tenue~sexe) %>% 
  hypothesize(null='independence') %>%
  calculate(stat='Chisq') %>% 
  visualize(method = 'theoretical',
            obs_stat=chi_obs,
            direction = 'greater')

Exemple 3: test du Chi-2 en cas de non-respect des conditions d’application du test classique

Un test du χ² classique (c’est-à-dire reposant sur la distribution théorique du χ²) est construit en supposant que les effectifs croisés sont ‘suffisants’. Ainsi, quand certaines cases du tableau de contingence comprennent trop peu d’individus, appliquer un test du χ² peut causer un ‘warning’ stipulant que l’approximation du χ² peut être incorrecte.

Considérons par exemple un sous-jeu de données de fantaisie rassemblant uniquement les individus de noble extraction, et intéressons-nous au lien entre leur sexe et leur couleur de tenue:

fantaisie_princiere=filter(fantaisie, activite=='royaute')

fantaisie_princiere %>% 
  janitor::tabyl(sexe,tenue) %>% 
  janitor::adorn_percentages("col") %>% 
  janitor::adorn_pct_formatting(digits=2) %>% 
  janitor::adorn_ns()

##      sexe      bleue      noire        rose      verte
##   feminin 75.00% (3) 25.00% (1) 100.00% (2) 50.00% (3)
##  masculin 25.00% (1) 75.00% (3)   0.00% (0) 50.00% (3)

Je réalise un test du χ² « classique »:

montest3 <- fantaisie_princiere %>%
  chisq_test(tenue~sexe) 

## Warning in stats::chisq.test(table(df), ...): Chi-squared approximation may be incorrect

montest3

## # A tibble: 1 x 3
##   statistic chisq_df p_value
##       <dbl>    <int>   <dbl>
## 1      3.81        3   0.283

Ici j’ai un warning car, de fait, certains niveaux croisés sexe*tenue comprennent très peu d’individus! Dans ce cas le recours à des permutations pour calculer la distribution de la statistique sous hypothèse d’indépendance s’avère très utile:

sim_princiere <- fantaisie_princiere %>%
  specify(tenue~sexe) %>% 
  hypothesize(null='independence') %>%
  generate(reps=1000, type='permute') %>% 
  calculate(stat='Chisq') 

Ici la p-value correspond à la proportion des cas (parmi les 1000 permutations) où la valeur de statistique observée sur données permutées a été supérieure à la statistique observée sur nos vraies données:

sim_princiere %>%
  get_pvalue(obs_stat = montest3$statistic,
             direction = "greater")

## # A tibble: 1 x 1
##   p_value
##     <dbl>
## 1   0.297

La distribution de la statistique du χ² pour ces permutations est montrée par l’histogramme.

sim_princiere%>% 
  visualize(obs_stat=montest3$statistic,
            direction='greater')

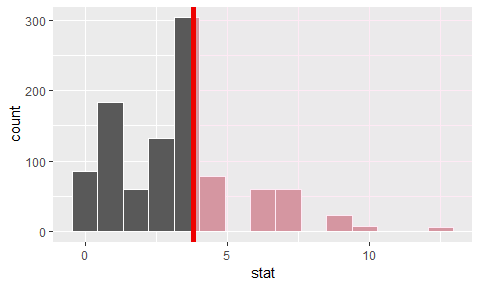
De fait, ici, on obtient une valeur de p-value extrêmement proche de celle que l’on avait obtenue en considérant la distribution théorique du χ²…