Chapitre 5 Résumer l’information par des métriques

Avant de réaliser quelques graphiques pour montrer le contenu lexical de nos textes il faudra la plupart du temps quelques calculs basiques sur nos données (par exemple agréger les données pour obtenir les fréquences d’occurrence des termes).

Pour réaliser ces quelques transformations on peut généralement utiliser les fonctions de dplyr.

5.1 Corpus MinisterEco

Dans la suite de cet ouvrage, nous considérerons un nouveau vrai corpus de textes correspondant à l’ensemble des communiqués de presse du Ministère de la Transition écologique et de la Cohésion des territoires mis en ligne ici.

Considérons les tables suivantes, qui résultent d’un travail de récupération (par web scraping), nettoyage, tokenisation, lemmatisation de ce corpus :

Ici, on repart du tableau tib_lemmes.

On pourrait être amené à

• calculer la fréquence des mots
• calculer la fréquence des mots pour différentes parties du corpus
• ne garder que les \(n\) mots les plus fréquents
• etc.

5.2 Fréquences d’occurrence

Le descripteur le plus basique que l’on puisse fournir concernant les lemmes est leur fréquence. On la calcule très simplement à l’aide des fonctions de dplyr:

freq_lemmes <- tib_lemmes %>%
  group_by(lemma) %>% 
  summarise(freq=n()) %>% 
  arrange(desc(freq)) %>% 
  na.omit()
head(freq_lemmes)

## # A tibble: 6 × 2
##   lemma       freq
##   <chr>      <int>
## 1 ministre    5046
## 2 écologique  3972
## 3 projet      3834
## 4 mettre      3138
## 5 presse      3044
## 6 permettre   2891

Bon. La version ci-dessus est la “version longue”, faite pour remobiliser les verbes de base de dplyr. Full disclosure: il existe une version raccourcie:

freq_lemmes=tib_lemmes %>% 
  count(lemma, sort=TRUE)
head(freq_lemmes)

## # A tibble: 6 × 2
##   lemma          n
##   <chr>      <int>
## 1 ministre    5046
## 2 écologique  3972
## 3 projet      3834
## 4 mettre      3138
## 5 presse      3044
## 6 permettre   2891

5.3 Table lexicale

Si l’on veut caractériser les fréquences de termes non pas dans l’absolu (dans le corpus entier) mais selon une partition du corpus on peut calculer la table lexicale:

tib_lex=table(tib_lemmes$lemma,tib_lemmes$ministre)
dim(tib_lex)

## [1] 8111    4

head(tib_lex)

##              
##               Barbara Pompili Élisabeth Borne François de Rugy Nicolas Hulot
##   aa                        0               1                0             0
##   abaissant                 1               0                0             0
##   abaissement               0               0                1             0
##   abaisser                  3               2                1             1
##   abandon                   7               5                3             3
##   abandonner                3               1               11             3

Ici la table lexicale porte sur l’ensemble des lemmes elle a donc pour dimension 8453 lignes (le nombre de lemme distincts) x 4 colonnes (le nombre de ministres).

La table lexicale ci-dessus permet ainsi de visualiser les effectifs croisés lemma * ministre. Cependant, pour toute analyse ultérieure de ces effectifs mieux vaut s’en tenir à une mise en forme “tidy” longue:

tib_lex_long=tib_lemmes %>% 
  group_by(lemma,ministre) %>% 
  summarise(n=n())
head(tib_lex_long)

## # A tibble: 6 × 3
## # Groups:   lemma [4]
##   lemma       ministre             n
##   <chr>       <chr>            <int>
## 1 aa          Élisabeth Borne      1
## 2 abaissant   Barbara Pompili      1
## 3 abaissement François de Rugy     1
## 4 abaisser    Barbara Pompili      3
## 5 abaisser    Élisabeth Borne      2
## 6 abaisser    François de Rugy     1

5.4 Co-occurrences, corrélations

Si l’on s’intéresse non plus seulement à la fréquence individuelle des termes mais qu’on cherche à caractériser les termes qui sont souvent employés ensemble (au sein d’un même document par exemple) on peut utiliser les fonctions du package widyr.

Considérons une paire de mots: motA et motB. - mot:T (pour TRUE) correspond à l’apparition du mot - mot:F (pour FALSE) correspond à la non-apparition du mot - \(N_{A=x,B=y}\) correspond à un effectif croisé des cas où motA:x (T ou F) et motB:y (T ou F)

	motA:T	motA:F	Total
motB:T	\(N_{TT}\)	\(N_{TF}\)	\(N_{T.}\)
motB:F	\(N_{FT}\)	\(N_{FF}\)	\(N_{F.}\)
Total	\(N_{.T}\)	\(N_{.F}\)	N

La fréquence de cooccurrence d’une paire mots correspond ainsi au nombre de fois où ces deux mots apparaissent dans une même entité (ci-dessous, le “doc”). En se référant au tableau ci-dessus, il s’agirait de \(N_{TT}\)

Pour calculer les cooccurences et corrélations (un processus assez calculatoire) je vais d’abord filtrer tib_lemmes pour ne garder que les mots ayant une fréquence d’occurrence haute…

tib_lemmes_light <- tib_lemmes %>%
  group_by(lemma) %>% 
  mutate(n=n()) %>% 
  filter(n>1000) %>% 
  ungroup()
head(tib_lemmes_light)

## # A tibble: 6 × 10
##   doc   word       lemma   type  lien  titre date       month      minis…¹     n
##   <chr> <chr>      <chr>   <chr> <chr> <chr> <date>     <date>     <chr>   <int>
## 1 doc1  ministres  minist… nom   http… PFUE… 2022-01-14 2022-01-01 Barbar…  5046
## 2 doc1  cadre      cadre   nom   http… PFUE… 2022-01-14 2022-01-01 Barbar…  1619
## 3 doc1  française  frança… adj   http… PFUE… 2022-01-14 2022-01-01 Barbar…  1223
## 4 doc1  européenne europé… adj   http… PFUE… 2022-01-14 2022-01-01 Barbar…  1449
## 5 doc1  presse     presse  nom   http… PFUE… 2022-01-14 2022-01-01 Barbar…  3044
## 6 doc1  ministère  minist… nom   http… PFUE… 2022-01-14 2022-01-01 Barbar…  1173
## # … with abbreviated variable name ¹​ministre

On utilise le package widyr (Robinson and Silge 2022) pour calculer les effectifs croisés:

library(widyr)
mots_cooc <- tib_lemmes_light %>% 
  pairwise_count(lemma,feature=doc,sort=TRUE)

head(mots_cooc)

## # A tibble: 6 × 3
##   item1      item2          n
##   <chr>      <chr>      <dbl>
## 1 écologique ministre    1416
## 2 ministre   écologique  1416
## 3 solidaire  écologique  1162
## 4 écologique solidaire   1162
## 5 solidaire  ministre    1035
## 6 ministre   solidaire   1035

La corrélation, quant à elle, correspond à :

\[Cor=\frac{N_{TT}N_{FF}-N_{TF}N_{FT}}{\sqrt{N_{T.}N_{F.}N_{.F}N_{.T}}}\]

mots_cors <- tib_lemmes_light %>% 
  pairwise_cor(lemma,doc,sort=TRUE)
head(mots_cors)

## # A tibble: 6 × 3
##   item1       item2       correlation
##   <chr>       <chr>             <dbl>
## 1 accréditer  presse            0.729
## 2 presse      accréditer        0.729
## 3 solidaire   écologique        0.643
## 4 écologique  solidaire         0.643
## 5 énergétique énergie           0.452
## 6 énergie     énergétique       0.452

Pour la suite on va joindre les tableaux mots_cooc et mot_cors

mots_cooc <- left_join(mots_cooc,
                       mots_cors,
                       by=c("item1","item2"))

5.5 TF-IDF

Le \(TF-IDF\) (pour “term frequency-inverse document frequency”) est une métrique qui reflète l’importance relative d’un mot dans un document.

• TF{d,w} est la fréquence (ou nombre d’occurrences) du terme \(w\) dans le document \(d\). Elle mesure l’importance du terme dans le document.
• IDF{d,w} est la fréquence inverse de document. Elle mesure l’importance du terme dans le corpus. Elle se calcule comme suit, où \(D\) est le nombre total de documents et \(\{d_j: w_i \in d_j\}\) est le nombre de documents qui contiennent le terme \(w_i\):

\[ IDF_{w}=log\left(\frac{D}{\{d_j: w_i \in d_j\}}\right)\] Le \(TF-IDF\) se calcule comme le produit \(TF*IDF\). La multiplication par \(IDF\) sert notamment à minimiser la valeur de \(TF-IDF\) pour les termes les plus fréquents, qu’on suppose peu discriminants.

tib_tfidf <- tib_lemmes %>% 
  count(doc,lemma) %>% 
  bind_tf_idf(lemma,doc,n) %>% 
  arrange(desc(tf_idf))

head(tib_tfidf, n=15)

## # A tibble: 15 × 6
##    doc     lemma           n    tf   idf tf_idf
##    <chr>   <chr>       <int> <dbl> <dbl>  <dbl>
##  1 doc2162 ficher          1 0.5    5.19  2.59 
##  2 doc2162 télécharger     1 0.5    4.63  2.31 
##  3 doc2574 télécharger     1 0.5    4.63  2.31 
##  4 doc2574 consulter       1 0.5    3.32  1.66 
##  5 doc2237 député          1 0.5    3.16  1.58 
##  6 doc2561 stand          11 0.282  4.38  1.23 
##  7 doc324  décryptage      1 0.167  7.27  1.21 
##  8 doc929  actif           1 0.333  3.35  1.12 
##  9 doc2558 joint           1 0.2    5.48  1.10 
## 10 doc2237 rapport         1 0.5    2.12  1.06 
## 11 doc929  perspective     1 0.333  2.98  0.995
## 12 doc2704 salon           2 0.222  4.18  0.928
## 13 doc2710 pack            1 0.125  7.27  0.909
## 14 doc1455 froid           1 0.2    4.53  0.905
## 15 doc2558 pièce           1 0.2    4.53  0.905

5.6 Spécificités

Le package textometry (Lafon, Pierre 1980) comprend une fonction qui permet de calculer des scores de spécificité (TXM Team 2013). Le but de ce score est (comme pour le TF-IDF) d’identifier les termes spécifiques à une partie du corpus.

Le modèle probabiliste associé à cet indice est expliqué [ici] (https://txm.sourceforge.net/doc/manual/0.7.9/fr/manual59.xhtml). On peut expliquer ce modèle à travers l’image de boules et d’urnes (oui oui, comme quand on fait des probabilités au lycée…).

Considérons ainsi que les mots dans des parties d’un texte sont assimilables à des boules dans des urnes. On s’interroge quant à la spécificité d’un mot particulier -boule rose- dans une partie du corpus -urne A-, autrement dit on se demande si le nombre de boules roses dans l’urne A ci-dessous pourrait être due à une distribution au hasard ou si au contraire cette fréquence relativement élevée démontre que les boules roses sont “spécifiques” de cette urne.

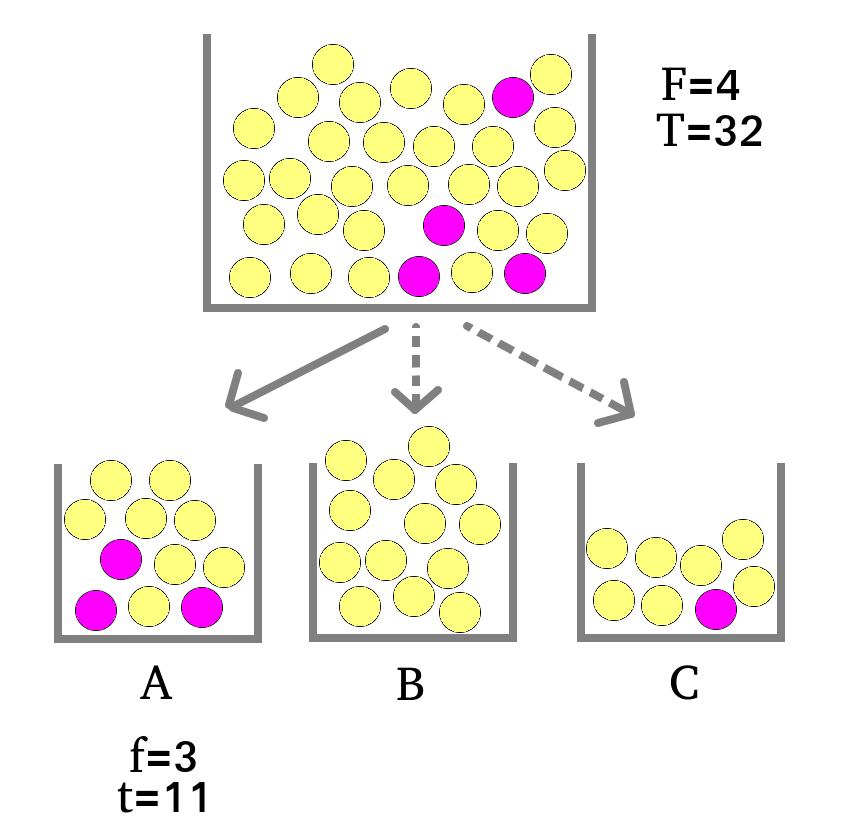
Pour calculer les chances d’observer cette fréquence simplement par hasard, on utilise la loi de probabilité hypergéométrique. Cette loi quantifie en effet la probabilité d’effectuer un tirage sans remise de \(f\) boules roses dans une urne/partie comprenant \(t\) boules en tout, en tirant dans un nombre total de boules de \(T\) boules dont \(F\) boules roses.

Dans l’exemple ci-dessus on a:

• \(f=3\) le nombre de boules roses dans A
• \(t=11\) le nombre de boules dans A
• \(F=4\) le nombre total de boules roses
• \(T=32\) le nombre total de boules

La probabilité dans ce contexte de tirer 11 boules et d’obtenir 3 boules roses ou plus est de:

#pr(X>=3)=1-pr(X<2)
1-phyper(q=2,m=4,n=32-4,k=11)

## [1] 0.1055339

On observe donc une fréquence (3) qui n’est pas complètement improbable (\(pr(X>2)\approx11\)%) sous hypothèse d’une distribution au hasard des boules. En effet, par convention, on tend à considérer un événement très improbable si sa probabilité est inférieure à 5% voire 1%.

\[-log10(pr(X \geq f))\] On obtient ainsi l’ordre de grandeur négatif de la probabilité:

• \(-log10(0.01)=2\)
• \(-log10(0.001)=3\)
• \(-log10(0.00001)=5\)
• \(-log10(1e-100)=100\)
• etc.

Autrement dit, plus la fréquence est forte et improbable sous hypothèse de distribution au hasard, plus le score est élevé, et un score \(\geq\) 2 correspond à une probabilité \(\leq\) 1%. C’est ainsi usuellement cette valeur seuil qu’on utilise pour considérer le score de spécificité comme étant significatif.

Les spécificités peuvent évidemment être calculées à la volée pour l’ensemble des termes (et non terme par terme comme on l’a fait ci-dessus à des fins pédagogiques). On utilise pour cela la fonction specificities() du package textometry.

Pour plus de compatibilité avec le tidyverse on peut utiliser la fonction tidy_specificities() qui utilise la fonction du package textometry et reformatte la sortie de cette fonction pour renvoyer un résultat tabulaire conforme à la logique “tidyverse”.

tib_spec <- mixr::tidy_specificities(tib_lemmes,lemma, ministre)
head(tib_spec)

## # A tibble: 6 × 4
##   lemma         ministre         spec     n
##   <chr>         <chr>           <dbl> <int>
## 1 logement      Barbara Pompili 190.    819
## 2 délégué       Barbara Pompili 147.    470
## 3 heure         Nicolas Hulot    89.8   367
## 4 relancer      Barbara Pompili  88.8   377
## 5 barbara       Barbara Pompili  74.8   180
## 6 distanciation Barbara Pompili  61.2   193

References

Lafon, Pierre. 1980. “Sur La Variabilité de La Fréquence Des Formes Dans Un Corpus.” Mots 1 (1): 127–65. https://doi.org/10.3406/mots.1980.1008.

Robinson, David, and Julia Silge. 2022. Widyr: Widen, Process, Then Re-Tidy Data. https://CRAN.R-project.org/package=widyr.

TXM Team. 2013. TXM Manual. Lyon, France: ICAR Laboratory, Lyon University & CNRS. https://txm.gitpages.huma-num.fr/textometrie?lang=en.