Research

The physical phenomenon I am interested in is the large-scale dynamics of the atmosphere and ocean, and its role in climate. The theoretical idea underlying my work in this field is the possibility to predict, in a probabilistic sense, systems which are unpredictable in a deterministic sense. Below are several examples of ways in which these two threads haven been woven together in my work.

Rare events in climate

Rare events account for most of the damage due to weather and climate hazards, and they are among the most important impacts of climate change. Yet, many aspects of such events remain poorly understood, in large part due to lack of proper tools to overcome the difficulties specific to these events. A large part of my work on this topic aims at developing such tools, in order to be able to estimate the statistical properties of such events and to develop prediction capabilities.

These methodological developments rely on theory, numerical algorithms designed to sample rare events more efficiently in climate models, and statistical models, including machine learning approaches. The methods have been often tested in low-dimensional toy models, and recently I have worked on applications for heat waves, turbulence and renewable energy.

Abrupt climate change and bifurcations of the large-scale circulation

A fascinating problem in climate dynamics is the possibility for the Earth system to undergo abrupt transitions, occurring on timescales which do not correspond to known external forcings. Events of this kind are documented in paleoclimate proxies, and the possibility that they might happen in the near future is perhaps one of the blind spots of climate change projections. I am particularly interested in abrupt transitions related to bifurcations of the atmospheric and oceanic circulation. A paradigmatic example is the AMOC, but other potential tipping points are worthy of study.

An example related to the tropical atmospheric circulation is equatorial superrotation: it consists in the appearance of a westerly jet at the Equator, carrying more angular momentum than solid-body rotation at the surface. Superrotation is believed to be very general: it is observed on planetary atmospheres such as Venus, Jupiter, Saturn or Titan, as well as tidally-locked exoplanets like HD189733b or HD209458b. It may also have played a part in past climates on Earth, or might occur in a warm future climate. Recently, I have studied the nature of the transition to superrotation: is it smooth or abrupt? In the second case, once we reach the tipping point, superrotation subsists even if we reverse the perturbation which made the conventional circulation unstable (hysteresis phenomenon). Besides, spontaneous transitions between the two states may be possible, even before the tipping point is reached, due to atmospheric macroturbulence, thereby providing a mechanism for noise-driven abrupt climate change.

2D and geophysical turbulence

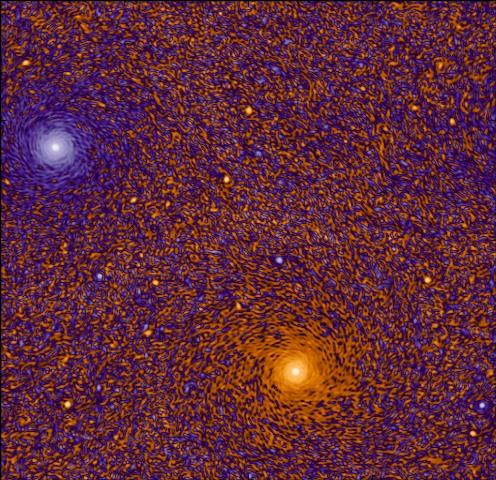
The behavior of fluid flow confined to a two-dimensional surface is of interest for at least two reasons.

At a fundamental level, such flows have a radically different behavior from their 3D counterpart, because they spontaneously organize into coherent structures, such as large scale vortices or jets. This is at variance with 3D turbulence, which is essentially a terribly efficient dissipation mechanism, sucking energy out of any background mean-flow. From a physical point of view, the crucial point is that vortex tubes can be stretched in a 3D flow, while this mechanism is forbidden in 2D. This property is reflected in the mathematical structure of the equations, which admit additional conservation laws (in the absence of forcing and dissipation) in 2D. These invariants account for the inverse cascade and for the existence of quasi-stationary states. Many classical methods of theoretical physics, which fail in 3D turbulence, provide insightful approaches to characterize the statistics of 2D turbulent fields. For instance, the system has non-trivial statistical equilibrium states, and perturbative methods allow to close the hierarchy of moments in a self-consistent way.

In addition to the theoretical motivations, these flows are worth studying because they provide, under minor modifications, a surprisingly good model for flows encountered in nature, such as planetary atmospheres or oceans. Indeed, the combination of geometrical confinement, rotation and density stratification makes geophysical flows akin to 2D flows. Although imperfect, this analogy has spurred major developments in geophysical fluid dynamics, such as geostrophic turbulence, and continues doing so.

A 2018 article in Quanta magazine, reprinted on Wired.com, puts this line of research in the spotlight.

Wave/vortex interactions in rotating-stratified flows

Both the atmosphere and the ocean are fully turbulent flows spanning a very broad range of length scales. The ocean for instance supports a thermohaline circulation at the planetary scale, on the order of ten thousand kilometers, western boundary currents such as the Gulf Stream and the Kuroshio, stretching over thousands of kilometers and surrounded by mesoscale rings of about 100 km diameter, as well as overturning and internal mixing occurring at scales as small as the centimeter. A fundamental question in geophysical fluid dynamics is to understand the energy pathway across this range of scales: how are large-scale circulations maintained? How do coherent structures such as mesoscale rings form? How are small-scale mixing and dissipation fed and how should we represent them in atmosphere and ocean models?

A major difficulty is that different processes dominate at different scales. This is at variance with more idealized turbulent flows, such as 3D homogeneous isotropic turbulence, for which the Kolmogorov theory predicts that large vortices break up into smaller vortices, and so on and so forth, down to the dissipation scale. In geophysical turbulence, the large scales of the flow are dominated by a balance between the Coriolis and the buoyancy forces and the pressure gradient. The behavior of these so-called 'geostrophic' vortices is very similar to that of a fluid on a two-dimensional surface: they tend to merge to form large-scale coherent structures. On the other hand, at very small scales, neither the Coriolis force nor the buoyancy force is felt any longer, and we expect the Kolmogorov theory of 3D turbulence to apply. In between, there exists a grey zone where the balanced motion coexists with much faster oscillatory motion referred to as inertia-gravity waves. The non-linearity of the equations leads not only to coupling between vortices of different size, as in geostrophic turbulence, but also between waves of different wavelength, and to interactions between vortices and waves.

My work on this topic aims at disentangling the role of vortices and waves in the energy transfer across the scales, using theoretical arguments and high-resolution numerical simulations. An important goal is to understand if, under certain circumstances, the range of scales can be divided into well-defined sub-ranges with universal energy spectrum and energy fluxes, like in the Kolmogorov theory.

See a slightly longer version of this text in the 2014 NCAR-ASP Annual Report