Poster Gallery
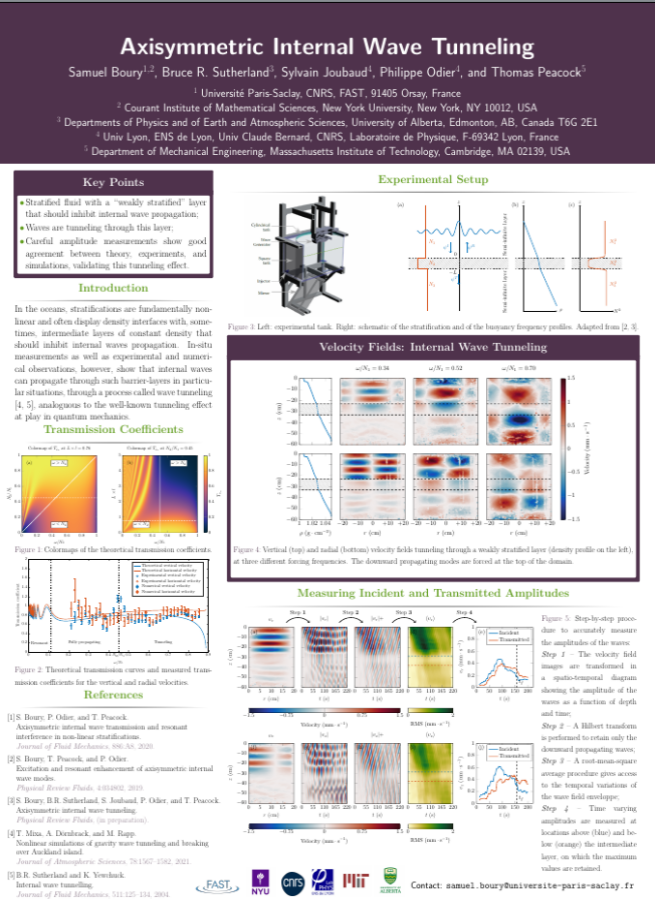
Axisymmetric Internal Wave Tunneling - RNL (2024)
S. Boury, B.R. Sutherland, S. Joubaud, P. Odier, and T. Peacock
Idealized linear stratifications, with constant density gradients, or piece-wise stratifications, linear by parts, are particularly interesting to understand and model the propagation of internal gravity wave through a column of stratified fluid. In the oceans, stratifications are fundamentally non-linear and often display density interfaces with, sometimes, layers of constant density that should inhibit internal waves propagation. In-situ measurements as well as experimental and numerical observations show that internal waves can propagate through such barrier-layers in particular situations, through a process called wave tunneling analoguous to the well-known tunneling effect at play in quantum mechanics. Combining experimental and numerical measurements, we show quantitatively that internal gravity waves can efficiently tunnel through constant density layers and still conserve their structure. We propose a simple three-layer model allowing for the computation of transmission coefficients for the velocity fields, and we test it on a case study. We notably show that there exists a smooth transition between the fully propagating and the tunneling regimes.
Wave Scattering and Irreversible Wave Capturing by Two-Dimensional Turbulent Flow - RNL (2023)
S. Boury, O. Bühler, and J. Shatah
Coupled wave-flow systems are prone to a wide variety of phenomena. Recently, several studies have shown that, in presence of a weak and stationary random mean flow, dispersive waves whose dispersion relation is a power law in k, may exhibit a "scattering" behaviour. In agreement with theoretical surveys, said scattering lies on the dispersion relation map in the phase space: the wave vector is rotating while its magnitude remains constant (and, consequently, so does the frequency). This process has been proposed for internal waves as well but, due to the particular nature of their dispersion relation, such result does not reflect the capability of the group velocity to evolve without changing the frequency, potentially breaking the fundamental assumption of a weak mean flow compared to the group velocity. In this work, we explore the elementary set of conditions that allows to obtain a scattering only in wave number orientation or both in wave number orientation and magnitude. We show that two regimes coexist with a non-trivial transition from one to the other. We demonstrate that there is a range of dispersive systems for which the frequency stays constant with a scattering only observed in wave number angle. However, for other systems the assumption that the group velocity is larger than the mean flow can break, yielding to a drift in frequency. This scattering is associated to an irreversible wave capturing process by the turbulent flow, the rays being trapped in large scale features. We also show that the existence of these regimes is robust by testing different turbulent flows and that the transition between them is modified when the mean flow becomes time-dependent.
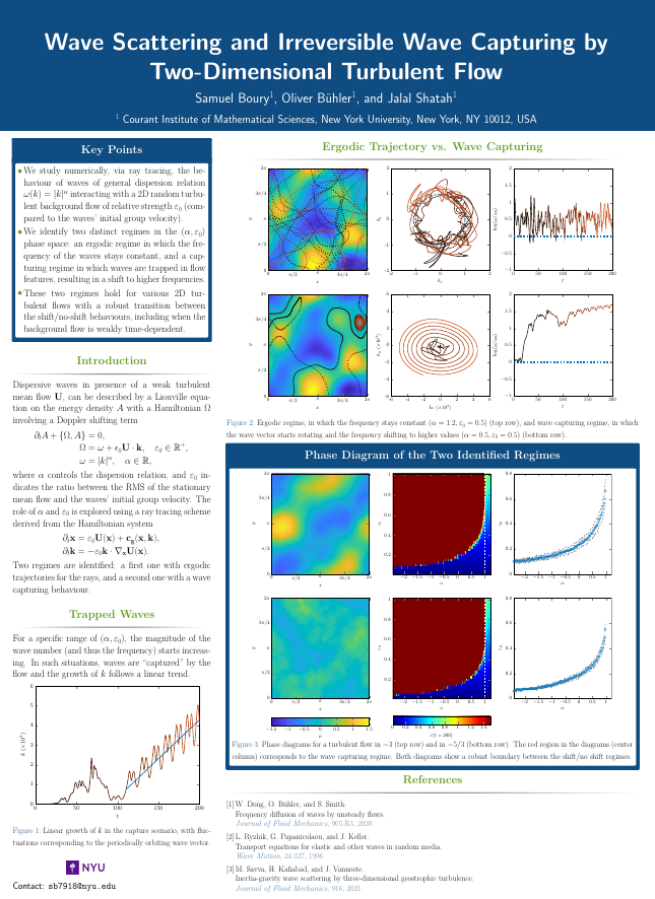
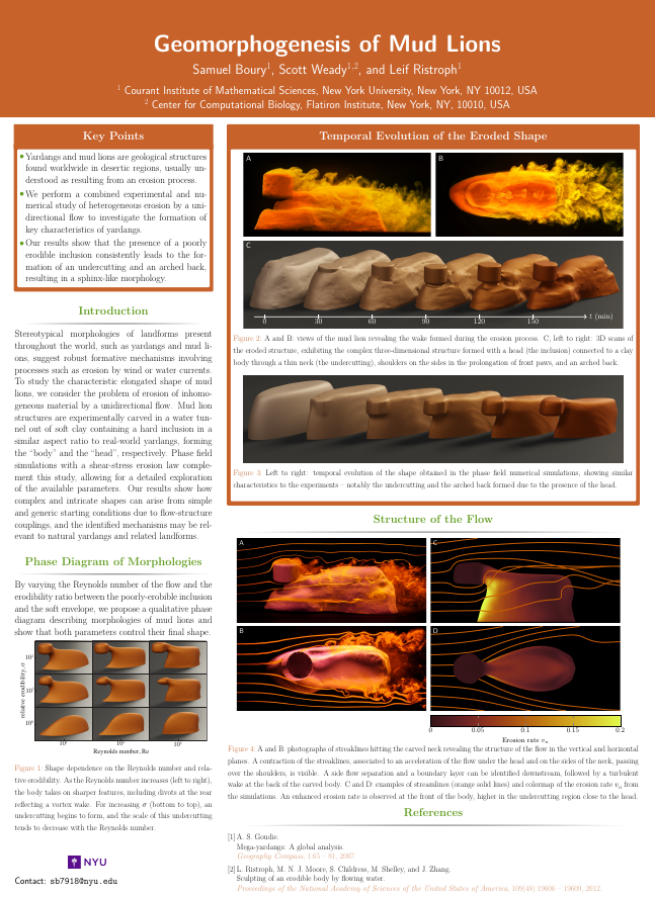
Geomorphogenesis of Mud Lions - AGU Fall Meeting (2022)
S. Boury, S. Weady, and L. Ristroph
Found in desert areas throughout the world, yardangs and mud lions constitute geological structures that exist in a wide variety of shape and sizes, but with a common overall morphology. Although recent studies have delved into their worldwide distribution and geological properties, their exact formation mechanism remains unexplained to this date. Based on field observations, however, it has been proposed that eolian erosion may play a central role in the carving of such structures. Through a combined use of laboratory experiments, conducted in a water tunnel, and of direct numerical simulations, using a phase-field model, we reproduce qualitatively the formation process of mud lions and propose a phase diagram describing their appearance. Mud lion structures are carved out of soft clay containing a hard inclusion in a similar aspect ratio to real-world yardangs, forming the “body” and the “head”, respectively. Our study demonstrates that both the Reynolds number of the flow driving the erosion process and the erodibility ratio between the solid, rocky inclusion and the soft, erodible envelope, drive the final morphology of the mud lion.
Sculpting the Sphinx - APS DFD, Gallery of Fluid Motion (2022)
S. Boury, S. Weady, and L. Ristroph
There is evidence that the Great Sphinx was a natural landform before its surface features were chiseled by the ancient Egyptians. Is this controversial theory plausible? We carried out experiments on the fluid mechanical erosion of clay. Based on accounts of the nonuniform composition of the Sphinx, we tested the effect of hard inclusions within hillocks of softer clay. The flow of a water tunnel mimics the prevailing winds of Giza, and three-dimensional optical scanning records the history and evolution of the shape as it erodes. A featureless mound transforms to a majestic lion in repose. The cylindrical head is the only inclusion, and its “wind shadow” shields the body. Dye added to the clay helps to visualize the turbulent wake that carves the back of the lion. Releasing dye upstream reveals compressed streaklines under the head, and this accelerated flow digs the neck and reveals the forelimbs and paws. These results show what ancient peoples may have encountered in the deserts of Egypt and why they envisioned a fantastic creature. Winner of Milton van Dyke poster award.
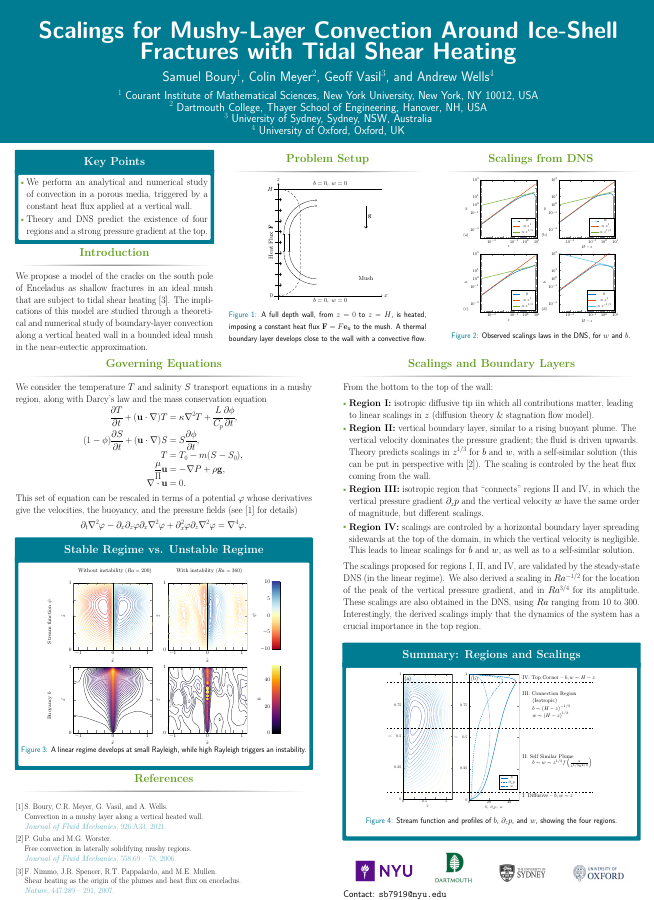
Scalings for Mushy-Layer Convection Around Ice-Shell Fractures with Tidal Shear Heating - AGU Fall Meeting (2021)
S. Boury, C.R. Meyer, G. Vasil, and A. Wells
We propose a model of the cracks on the south pole of Enceladus as shallow fractures in an ideal mush that are subject to tidal shear heating. In order to study the implications of this model on ice melting, we perform a theoretical and numerical study of boundary-layer convection along a vertical heated wall in a bounded ideal mushy region. The mush is comprised of a porous and reactive binary alloy with a mixture of saline liquid in a solid matrix, and is studied in the near-eutectic approximation. We demonstrate the existence of four different regions close to the crack with different dynamical balances in each, and study their behavior asymptotically. Starting from the bottom, the four regions are (i) an isotropic corner region; (ii) a buoyancy dominated vertical boundary layer; (iii) an isotropic connection region; and (iv) a horizontal boundary layer at the top boundary with strong gradients of pressure and buoyancy. The scalings obtained from direct numerical simulations run in Python with Dedalus are consistent with the theoretical predictions. Close to the heated wall, the convection in the mushy layer is similar to a rising buoyant plume abruptly stopped at the top, leading to increased pressure and temperature in the upper region. We discuss the impact as an eUcient melting mechanism that could be a relevant model for the impact of shear heating along the cracks of Enceladus.
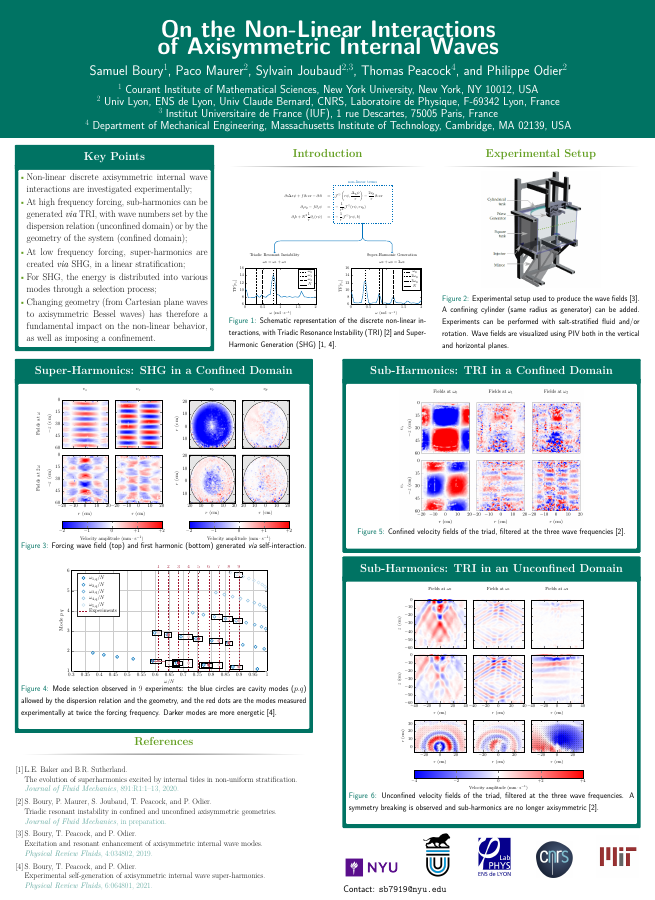
On the Non-Linear Interactions of Axisymmetric Internal Waves - AGU Fall Meeting (2021)
S. Boury, T. Peacock, P. Odier, S. Joubaud, and P. Maurer
Geophysical stratified fluids, such as the oceans, are suitable media for the propagation of inertia-gravity waves. Well-known for their intriguing properties, these internal waves are a key ingredient of the oceanic mixing, taking part in energy transfers from scale to scale through non-linear interactions. As of today, however, a vast majority of studies focuses on a plane wave formalism and are often restricted to two-dimensional geometries, disregarding many potential three-dimensional effects. Shifting geometry from a 2D Cartesian framework to a 3D axisymmetric domain, and therefore from plane waves based on exponential functions to cylindrical waves based on Bessel functions with radially decreasing amplitudes, offers an interesting perspective on the study of these waves. This innovative focus on internal waves actually brings up numerous differences regarding their non-linear interactions. A significant difference, for example, is that the non-linear self-interaction terms (expressed through Jacobians) are non-zero for pure axisymmetric wave fields, contrary to Cartesian plane waves. Thanks to a versatile cylindrical experimental apparatus and an axisymmetric wave generator, we are able to shed light on these peculiar wave-wave interactions. Supported by theoretical studies, our experimental observations show that, in some cases, the self-interaction of the wave can lead to the generation of super-harmonics (SHG), but in other cases non-linear effects can lead to the excitation of sub-harmonics via Triadic Resonant Interaction (TRI). In both cases, the presence of physical boundaries, or confinement, plays a role in the selection of the wave field structure: while resonances set the wave numbers in unconfined domains, symmetry and boundary conditions prevail in confined setups.
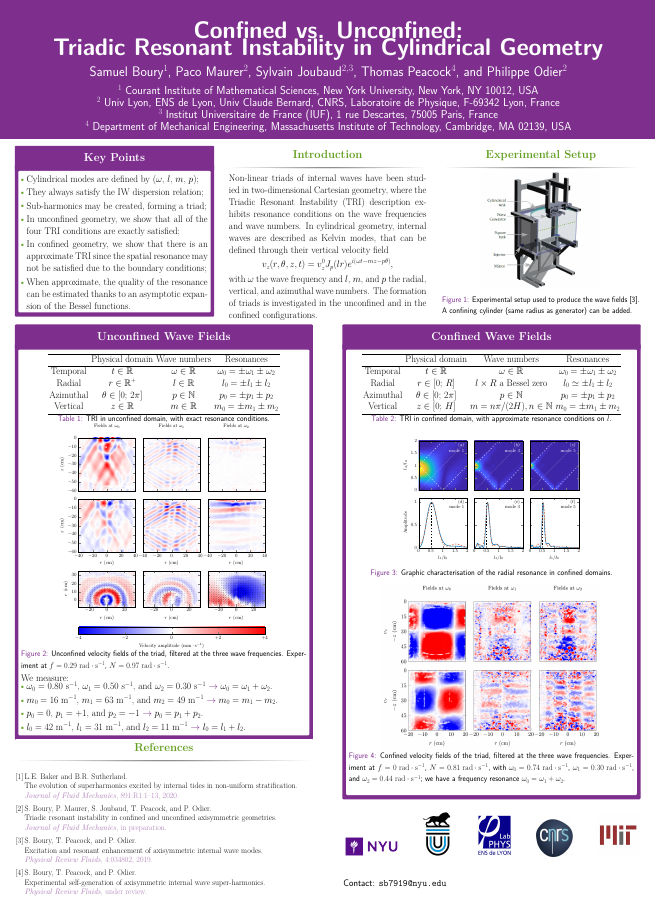
Confined vs. Unconfined: Triadic Resonant Instability in Cylindrical Geometry - RNL (2021)
S. Boury, P. Maurer, S. Joubaud, T. Peacock, and P. Odier
The various non-linear mechanisms through which inertia-gravity waves can be excited at different frequencies and different wave numbers trigger an on-going interest since they are associated to energy transfers from scales to scales and may have a significant role in mixing processes, for example in the oceans. Among these non-linear interactions is the spontaneous generation of sub-harmonics forming resonant a triad with the primary wave field, called Triadic Resonant Interaction (TRI). Numerous experimental, numerical, and theoretical studies have been conducted to investigate TRI and sub-harmonics in 2D Cartesian geometry, using plane wave formalism. The triads constituted of the forced wave and the two spontaneously excited sub-harmonics are then found to satisfy a linear resonance condition, both on the frequencies and on the wave numbers. With axisymmetric internal waves in cylindrical geometry, however, the description of the wave field in terms of Bessel functions yields more complicated equations and it is not obvious that the same TRI conditions are satisfied. While evidence of TRI in such geometries have been reported recently, no clear theory has been derived to characterise the corresponding resonance conditions. In an unconfined 3D configuration, we derive the relevant resonance conditions cylindrical wave fields satisfy and we show that they are similar to the TRI ones for Cartesian plane waves, although the radial resonance is only approximate. We also show that, when the waves are fully confined, boundary condition prevail, leading to a triad of waves that are non-necessarily spatially resonant. Using an apparatus that has been proven capable of generating axisymmetric internal wave fields, we present experimental observations of axisymmetric internal wave sub-harmonics generated in unconfined and confined domains, agreeing well with the proposed theory.
Whither the Chukchi Slope Current? - OSM (2020)
S. Boury, P. Odier, R.S. Pickart, P. Lin, M. Li, E.C. Fine, J.A. MacKinnon, and T. Peacock
From the Pacific Ocean through the Bering Strait, the pathways by which water ultimately inflows to the Arctic Ocean via the Chukchi Shelf are of great interest for improving current understanding of the evolving state of the Arctic Ocean, as the fate of warm waters can influence melting processes. In this study, through the combined use of shipboard ADCP data and five SOLO floats deployed as Lagrangian tracers, we delve further into the trajectory and the fate of the newly discovered Chukchi Slope Current (CSC), that accounts for a large part of the inflow off the Shelf through Barrow Canyon. We show that the CSC is a persistent current carrying hot and fresh water, that follows closely the bathymetry of the Chukchi Shelf, consistent with previous studies. Our data set demonstrate that it goes far North beyond the Northwind Ridge until ice-covered regions. Through its journey, the CSC experiences either atmospheric events (wind driven stresses, that can reinforce, weaken or reverse the current) or oceanographic disruption (eddy-current interaction, providing cold water to the current and supporting lateral mixing) that impacts its volume transport and strongly supports mixing of its heat content with cold Arctic waters.
Whither the Chukchi Slope Current? - ENS students meeting (2019)
S. Boury, T. Peacock, P. Odier, J.A. MacKinnon, and R.S. Pickart
Recent measurements and modeling indicate that roughly half of the Pacific-origin water exiting the Chukchi Sea shelf through Barrow Canyon forms a westward-flowing current known as the Chukchi Slope Current (CSC), yet the trajectory and fate of this current is presently unknown. In this study, through the combined use of shipboard velocity data and information from five profiling floats deployed as quasi-Lagrangian particles, we delve further into the trajectory and the fate of the CSC. During the period of observation, from early September to early October 2018, the CSC progressed far to the north into the Chukchi Borderland. The northward excursion is believed to result from the current negotiating Hanna Canyon on the Chukchi slope, consistent with potential vorticity dynamics. The volume transport of the CSC, calculated using a set of shipboard transects, decreased from approximately 2 Sv to near zero over a period of 4 days. This variation can be explained by a concomitant change in the wind stress curl over the Chukchi shelf from positive to negative. After turning northward, the CSC was disrupted and four of the five floats veered offshore, with one of the floats permanently leaving the current. It is hypothesized that the observed disruption was due to an anticyclonic eddy interacting with the CSC, which has been observed previously. These results demonstrate that, at times, the CSC can get entrained into the Beaufort Gyre.
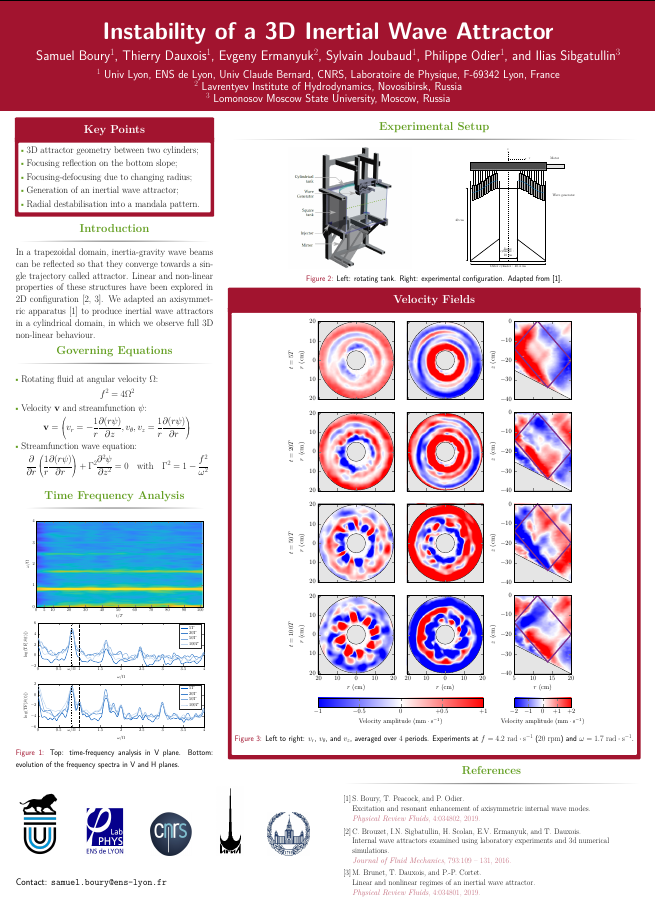
Instability of a 3D Inertial Wave Attractor - RNL (2019)
S. Boury, T. Dauxois, E. Ermanyuk, S. Joubaud, P. Odier, and I. Sibgatullin
For a few decades now, numerous studies have been devoted to the intriguing properties of inertia-gravity wave reflection. Since the angle of propagation of these waves is set by the ratio of their frequency to the buoyancy or rotation frequency, the reflection on a wall does not follow the usual Snell-Descartes law. In particular, in a confined trapezoidal geometry, when one of the walls is neither horizontal nor vertical, the wave beam experiences a focusing effect and eventually, whatever the initial source of the waves, ends on a definite trajectory called attractor. Experimental and numerical studies have shown evidence of this structure for internal gravity waves and for internal inertial waves in 2D geometry . Due to the local energy focusing, non-linear triadic cascades occur in the branches of the attractor, leading to energy transfer between scales, which has been observed experimentally. More recently, geometric and 3D aspects of internal wave attractors have been explored using numerical simulations with inertial waves. Direct numerical simulations pictured an axisymmetric inertial wave attractor, in a trapezoidal cylindrical domain, in which focusing and defocusing effects are caused by the reflection on the inclined wall, as well as by the radially expanding geometry itself. Wave instability occurs while forcing the attractor, leading to a destabilised flow and a symmetry breakdown. Using an experimental apparatus that has shown relevance for axisymmetric wave generation, we produce an inertial wave attractor in a cylindrical domain and we explore its properties.
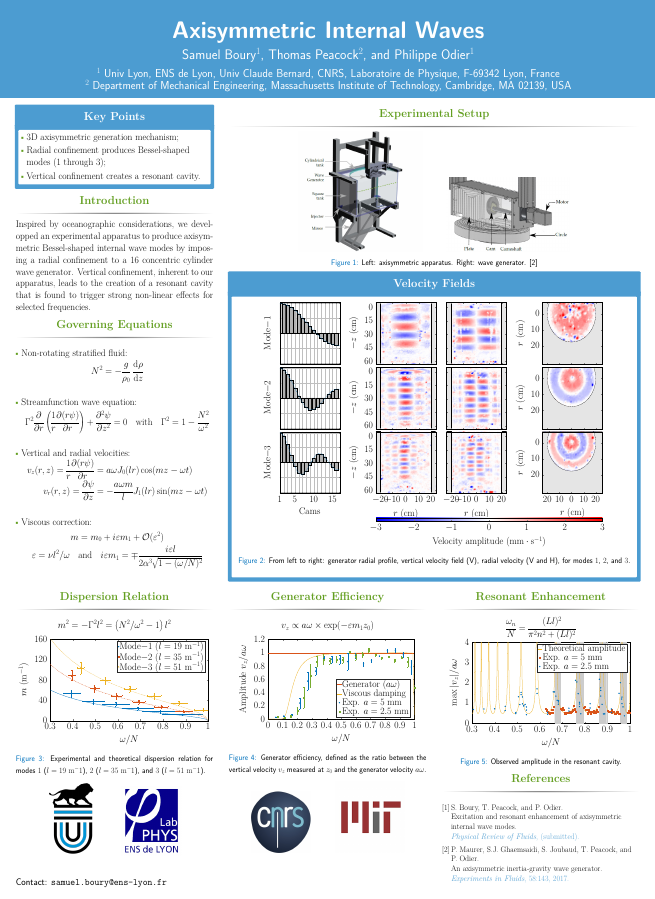
Axisymmetric Internal Waves - Houches (2019)
S. Boury, T. Peacock, and P. Odier
To date, axisymmetric internal wave fields, which have relevance to atmospheric internal wave fields generated by storm cells and oceanic near-inertial wave fields produced by surface perturbations, have been experimentally realized using an oscillating sphere or torus as the source. Here we use a wave generator configuration capable of exciting axisymmetric internal wave fields of arbitrary radial form to generate axisymmetric internal wave modes. After establishing the theoretical background for axisymmetric mode propagation, taking into account lateral and vertical confinement, and also accounting for the effects of weak viscosity, we study modes of different order. We characterize the efficiency of the wave generator through careful measurement of the wave amplitude based upon group velocity arguments, and then consider the effect of vertical confinement to induce resonance, identifying a series of experimental resonant peaks that agree well with theoretical predictions. In the vicinity of resonance, the wave fields undergo a transition to nonlinear behavior that is initiated on the central axis of the domain and proceeds to erode the wave field throughout the domain.