Tsunamis et vagues solitaires
L'expérience et les résultats présentés sur cette page font partie du travail du laboratoire junior "Géophysique et fluides planétaires." Ils ont été publiés en ligne en 2016 (Brouzet et al. Fabriquons des tsunamis ! Culture sciences physiques, 2016 [4]) et dans le Bulletin de l'Union des Physiciens en 2020 (Boury et al. Vagues solitaires : tsunamis en laboratoire. Bulletin de l'Union des Physiciens, à paraître [2]). Je remercie chaleureusement toutes les personnes ayant été amenées à participer à ce projet : C. Brouzet, M. Lasbleis, P. Maurer, L. Menou, R. Menu, H. Piot-Durand, J. Thibaut et V. de Zotti. Cette page a été créée à l'occasion des TIPE (Travaux d'Initiative Personnelle Encadrés) 2019-2020, dont le thème est "l'océan". Merci de respecter le droit d'auteur et de citer les différentes références.
Résumé
Longtemps inexpliqués, les tsunamis sont aujourd'hui des phénomènes océaniques relativement bien compris, notamment depuis la découverte des solitons, ou ondes solitaires, hydrodynamiques par John Scott Russel au milieu du XIXème siècle. Imprévisibles et potentiellement dévastatrices lorsqu'elles arrivent sur les côtes, ces vagues géantes font courir des risques importants aux populations installées sur le littoral : les comprendre et s'en protéger est un enjeu important dans un monde où plus de la moitié de la population réside sur les côtes. Le texte suivant présente un dispositif expérimental simple permettant de reproduire qualitativement le phénomène de tsunami et d'en étudier quantitativement différents aspects comme la vitesse de propagation ou le déferlement. Un modèle théorique, basé sur l'équation non linéaire de Korteweg-de Vries, est également proposé.
1. Introduction
Des vagues géantes se forment parfois et déferlent sur les côtes : ce sont des tsunamis, terme japonais désignant des « vagues du port », fréquemment observées dans l'archipel. Décrite comme une grande vague arrivant seule sur le littoral, parfois suivie de répliques plus petites, sa hauteur de plusieurs mètres (ou dizaines de mètres) et sa vitesse importante la rendent extrêmement dangereuse et dévastatrice. Ce type de vague appartient à la catégorie des ondes solitaires, et sont créées dans l'océan par des événements très énergétiques et souvent soudains : par un séisme, provoquant brusquement un déplacement d'eau sous-marin, ou par la chute d'objets très massifs dans l'eau comme une météorite ou des blocs de glace dans les fjords.
L'étude et la compréhension des tsunamis est d'autant plus importante aujourd'hui du fait de la densification de l'habitat sur les côtes et de l'installation d'équipements et d'infrastructures potentiellement sensibles, dont l'endommagement aurait des effets néfastes pour l'homme et l'environnement : par exemple, des industries chimiques ou des centrales nucléaires (l'accident nucléaire de Fukushima est justement une conséquence du tsunami de 2011 provoqué par un séisme ayant eu lieu au large du Japon). À terme, une meilleure connaissance des tsunamis permettrait d'en améliorer la prévention, la détection et d'en limiter les dégâts.
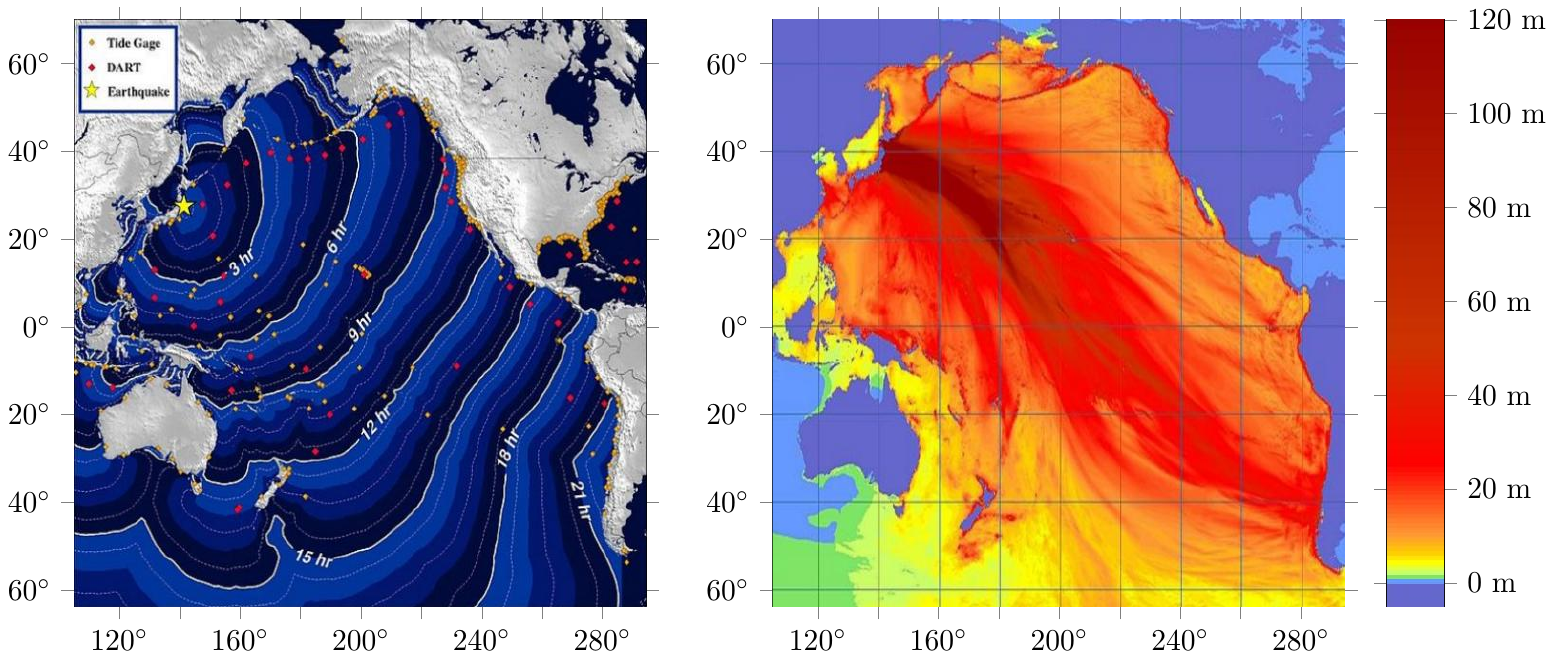
Figure 1 – Temps de propagation (gauche) et amplitude (droite) de la vague du tsunami généré lors du séisme de Sendai (Japon), le 11 mars 2011. Ce tsunami est notamment à l’origine de la catastrophe nucléaire de Fukushima. Source : Wikipedia et NOAA.
Pour modéliser le phénomène des tsunamis, différentes étapes doivent être considérées : une première phase de génération de l'onde, plutôt localisée en haute mer, suivie d'une phase de propagation en haute mer et d'une derniére phase de déferlement située, elle, près des côtes. Les parties suivantes détaillent une étude expérimentale ainsi que des considérations théoriques permettant d'approcher la physique des tsunamis.
2. L'expérience : protocole et dispositif expérimental
Les expériences ont été réalisées dans une cuve en plexiglas de longueur 200 cm, de hauteur 40 cm et de largeur 20 cm. Sa faible largeur comparée à sa longueur permet de considérer, en première approximation, un océan à deux dimensions (hauteur et longueur) dans lequel l'onde de surface ne se propage que selon une direction (celle de la longueur). La cuve est remplie d'eau jusqu'à une hauteur h, qui peut donc être ajustée d'une expérience à l'autre, et a été colorée à l'aide d'un colorant alimentaire bleu pour permettre des mesures précises des déplacements de la surface libre. L'expérience est présentée figure 2.
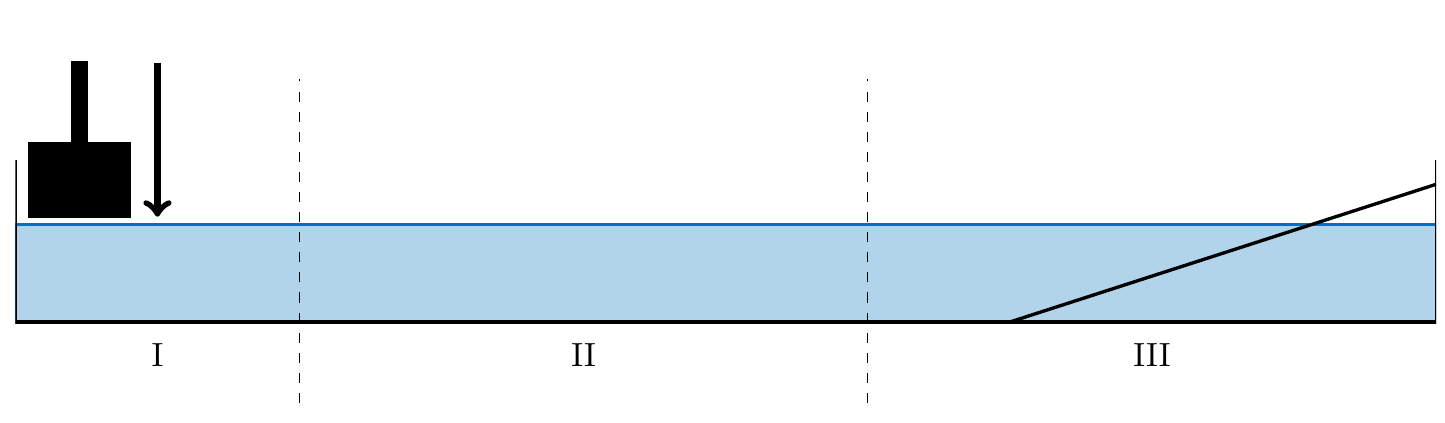
Figure 2 – Schéma du dispositif expérimental, avec les régions de génération (I), de propagation (II) et d'arrivée de l'onde (III).
L'expérience peut être divisée en plusieurs régions :
-
La génération de l'onde, près du bord gauche de la cuve (région I). La création de l'onde est assurée par un déplacement brusque d'un grand volume d'eau, obtenu grâce à un marteau (un bloc de plexiglas) lâché au niveau de la surface libre, sans vitesse initiale. L'énergie injectée dans le fluide est supposée être la même dans chaque réalisation de l'expérience. Ce mécanisme est similaire à celui proposé dans Remoissenet [9] où un volume d'eau est relâché à une extrémité de la cuve.
-
La propagation de l'onde, dans la partie centrale de l'expérience (région II). Cette phase constitue le régime stationnaire de l'onde. Les effets de bords y sont négligés et la hauteur d'eau au repos h y est constante.
-
L'arrivée sur la pente et le déferlement de l'onde, à l'extrémité droite de la cuve (région III). L'onde arrive sur une plaque de plexiglas amovible, partiellement immergée, d'inclinaison variable : la pente ainsi créée simule un littoral, où la hauteur d'eau diminue progressivement.
Une caméra est installée parallèlement à la face principale de la cuve pour visualiser l'onde.
Les trois prochaines sections portent sur l'étude de ces différents domaines.
3. Génération de l'onde
Dans cette expérience, la génération de l'onde est assurée par un déplacement d'eau brusque créé par un marteau lâché au niveau de la surface de l'eau, sans vitesse initiale. En plongeant, ce marteau provoque le déplacement d'un volume d'eau (égal au volume occupé par le marteau lui-même) tout en injectant de l'énergie dans le système. Cette énergie est égale à la différence d'énergie potentielle du marteau et peut être reliée à l'énergie de l'onde. Des mécanismes similaires, comme la libération brutale d'un volume d'eau [9] peuvent aussi générer de telles ondes, mais ne permettent pas de reproduire l'expérience indéfiniment avec la même hauteur d'eau initiale.
Le dispositif assure qu'une seule onde est créée et puisse se propager dans la cuve.
4. Propagation de l'onde
Dans l'expérience, la vague générée se propage d'une extrémité de la cuve à l'autre, et consiste en une déformation de la surface libre. Pour un fluide supposé parfait et incompressible, ayant une masse volumique ρ et un coefficient de tension de surface γ, soumis à un champ de pesanteur g, sa dynamique est donnée par la contribution de différents termes :
-
La force de pesanteur, agissant à grande échelle, visant à rétablir l'équilibre hydrostatique;
-
La force liée à la tension de surface, à petite échelle, qui tend à privilégier des interfaces ayant la plus petite superficie, correspondant ici à une interface horizontale plane;
Ensemble, ces contributions gouvernent la physique des ondes gravito-capillaires. En partant des équations de Navier-Stokes, la relation de dispersion suivante, reliant la pulsation de l'onde ω à son vecteur d'onde k, peut être établie [7, 9] :
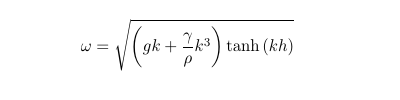
Ici, les longueurs d'ondes considérées sont suffisamment grandes pour que la partie capillaire soit négligeable devant la partie gravité de l'onde. La relation de dispersion peut donc être simplifiée et permet d'obtenir la vitesse de la vague en faisant le rapport de la pulsation sur le nombre d'onde :
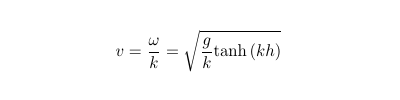
Un développement limité de la tangente hyperbolique permet de discuter un peu plus cette expression. À l'ordre le plus bas en kh, la célérité de l'onde, notée c par la suite, est ainsi :
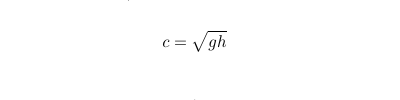
Cette expression de la vitesse est valide dans un modèle en eau profonde, lorsque la perturbation de la surface engendrée par la vague de hauteur η est petite devant la hauteur d'eau au repos h, ce qui n'est pas le cas dans l'expérience comme discuté ci-après. Une correction prenant en compte l'influence de la hauteur de la vague est donnée par [9] :
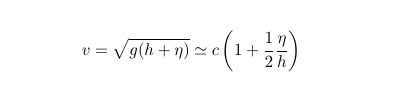
De façon plus générale, la relation de dispersion complète, tenant compte des termes non linéaires et de la dispersivité, est liée à l'équation de Korteveg-de Vries :
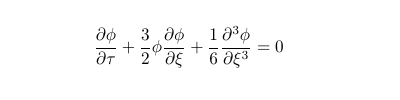
exprimée en fonction de variables sans dimensions, où φ est l'amplitude de la vague, τ le temps et ξ la variable d'espace dans le référentiel de l'onde. Comme détaillé par Brouzet et al. [4], cette équation comporte différents termes dont les contributions peuvent être expliquées comme suit :
-
Un terme d'évolution temporelle, la dérivée temporelle de φ;
-
Un terme correspondant à une propagation dispersive, la dérivée troisième de φ par rapport à la coordonnée d'espace ξ, qui a tendance à aplatir la vague et donc à limiter la croissance de l'amplitude;
-
Un terme non linéaire, le produit de φ et sa dérivée spatiale, favorisant un resserrement de la vague et une augmentation de son amplitude.
L'équation est intégrable et admet une solution exacte en sinus hyperbolique dépendant des variables adimensionnées ξ et τ et s'écrivant
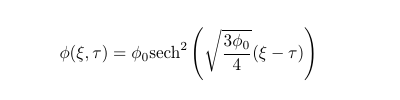
Cette solution décrit de manière satisfaisante le phénomène observé dans l'expérience, comme le montre la figure 3. Il s'agit d'une onde solitaire de type soliton se propageant selon les abscisses positives. Une seconde solution existe également, décrivant des ondes périodiques appelées ondes cnoïdales plus adaptées dans un modèle en eau peu profonde.
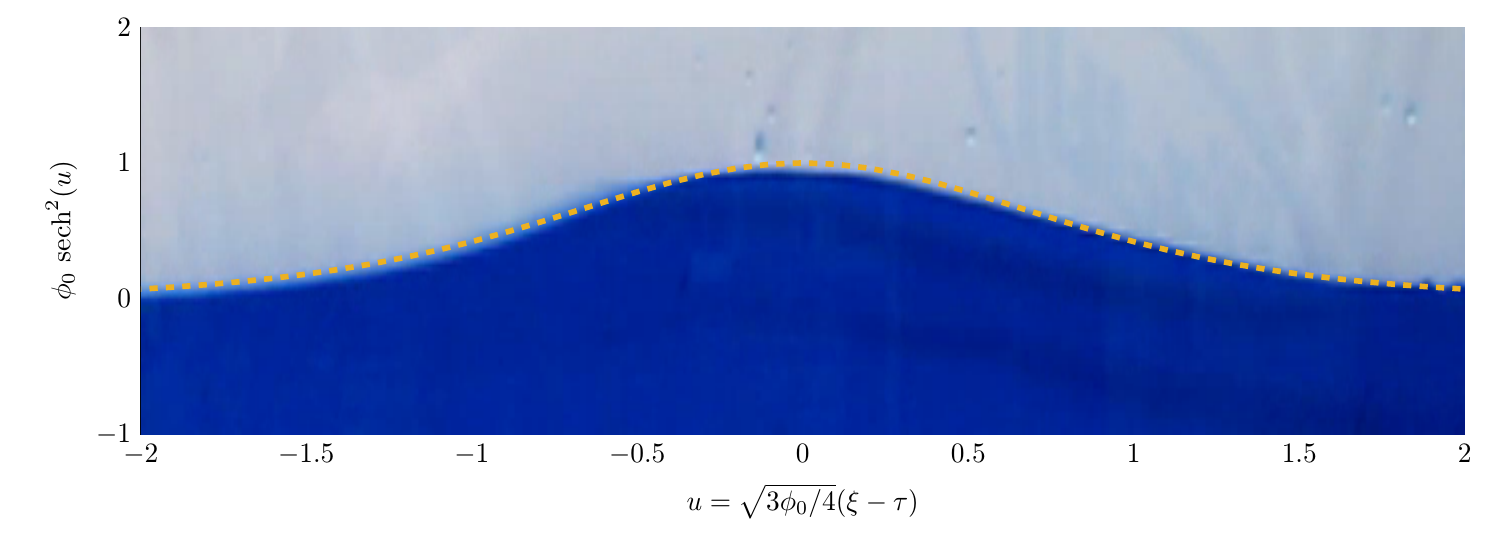
Figure 3 – Modèle théorique, solution des équations de Korteweg-de Vries (courbe jaune en pointillés) superposé à une vague solitaire créée expérimentalement et se propageant librement dans la cuve (hauteur d'eau au repos 8cm).
Pour caractériser davantage la vague formée, d'autres mesures quantitatives peuvent être effectuées comme, par exemple, la hauteur de la vague η (figure 4, gauche) et sa vitesse v (figure 4, droite) en fonction de la hauteur d'eau au repos h. Ces mesures sont très reproductibles, malgré une certaine dispersion probablement liée au mécanisme de génération de l'onde.
Pour des hauteurs d'eau h relativement petites (inférieures à 6 cm), la hauteur de la vague augmente. Elle arrive à saturation à η = 4 cm pour de plus grandes hauteurs d'eau au repos, et reste dès lors constante (voir figure 4 gauche). En parallèle, l'étalement longitudinal de la vague (non présenté ici), initialement constant, croît pour des hauteurs d'eau au repos supérieures à 6 cm. La hauteur de la vague η est non négligeable par rapport à la hauteur d'eau h, leur rapport variant de 50% à 25%. Alors que dans un modèle en eau profonde il est possible de négliger η devant h, ce n'est pas le cas ici, et la hauteur pertinente qu'il faut considérer pour cette étude est ainsi h+η.
La vitesse de la vague, notée v, est mesurée en regardant le déplacement du sommet de la vague sur des images successives. Compte tenu de la remarque précédente, l'étude de la vitesse de l'onde ne se fait pas en fonction de h mais de h+η. La figure 4 droite montre l'évolution du carré de la vitesse en fonction de cette hauteur caractéristique h+η. Une régression affine donne alors un très bon accord avec les points expérimentaux, conformément à la vitesse théoriquement prédite indiquée dans les développements précédents.
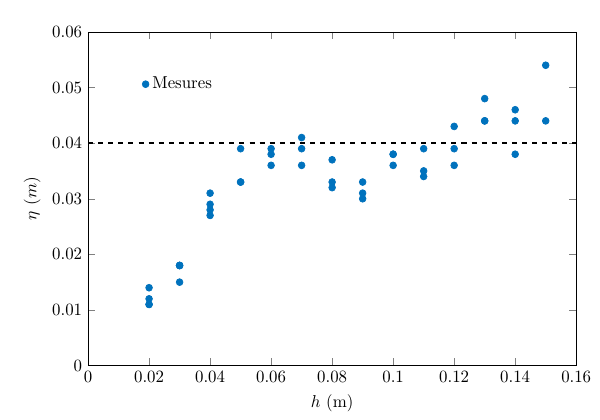
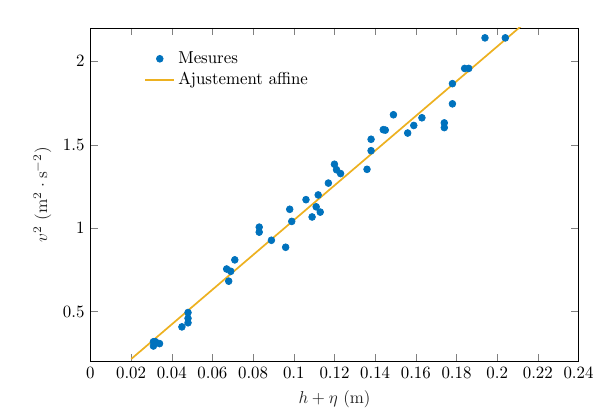
Figure 4 – Gauche : évolution de la hauteur de la vague η (en m) en fonction de la hauteur d'eau au repos h (en m). Droite : carré de la vitesse de la vague v (en m/s) en fonction de la hauteur d'eau au sommet de la vague h+η (en m), et ajustement affine.
5. Arrivée sur la côte et déferlement
Les tsunamis sont essentiellement connus pour les vagues dévastatrices qu'ils provoquent en arrivant sur les côtes. Ce phénomène est étudié dans l'expérience proposée grâce au plan incliné partiellement immergé présent à l'extrémité droite de la cuve.
Les déferlements ne sont pas systématiquement observés : comme le montre la figure 5, certaines vagues déferlent (à gauche), quand d'autres se contentent de glisser le long de la pente (à droite). Les observations expérimentales montrent que la vague ne forme un rouleau et ne déferle que si l'angle d'inclinaison de la pente avec l'horizontale est suffisamment faible. De fait, pour ces conditions expérimentales, les déferlements n'ont pu être observés que pour un angle d'inclinaison inférieur à 8°.


Figure 5 – Gauche : exemple d'un cas avec déferlement, lorsque l'inclinaison de la pente n'est pas trop grande. Droite : exemple d'un cas sans déferlement, lorsque l'inclinaison de la pente est trop importante.
Airy [1] a proposé une explication simple du mécanisme de déferlement. Dans l'équation de Korteweg-de Vries, le terme non linéaire a une contribution en l'inverse de h, qui peut devenir très importante lorsque la hauteur d'eau au repos est peu profonde. Ce terme agit comme un amplificateur : sa contribution tend à diminuer l'étendue longitudinale de la vague tout en la faisant croître verticalement, et cet effet devient d'autant plus important que l'amplitude de la vague est grande. Lorsque la vague monte sur la pente, la hauteur h diminue et la contribution des termes non linéaires devient encore plus importante, conduisant à l'augmentation de l'amplitude η de la vague.
De façon qualitative, la déstabilisation peut s'expliquer à partir de l'expression de la vitesse de la vague :
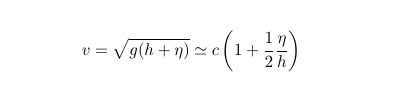
suggérant une variation de la vitesse de la vague avec sa hauteur. Le sommet, pour lequel η est plus grand, avance ainsi plus vite que le reste de la vague et notamment que sa base. Elle devient asymétrique et tend à basculer en avant pour, à terme, si l'amplitude est suffisamment importante, se casser et déferler [1, 9].
6. Conclusion
L'expérience proposée ici permet de modéliser simplement une vague solitaire, de type tsunami, avec sa génération, sa propagation et son éventuel déferlement sur les côtes. Différentes caractéristiques des tsunamis, en lien avec la physique des ondes, peuvent ainsi être mises en évidence : déplacement d'énergie et non de matière, longueur d'onde, célérité... De plus, le dispositif présenté montre qu'en arrivant sur le littoral (en pente plus ou moins douce) la hauteur de la vague augmente et peut mener à un phénomène de déferlement, potentiellement très dangereux.
L'influence de nombreux paramètres pourrait être explorée plus en détail, comme la notion d'onde cnoïdale pour le déplacement en surface, les aspects énergétiques (notamment lors de la génération de l'onde, jusqu'à son déferlement) ou l'étalement longitudinal de la vague. En utilisant deux marteaux pour générer une onde à chaque extrémité il est également possible d'étudier l'interaction de deux ondes se propageant selon la même direction mais en sens opposé. Enfin, l'introduction d'objets au fond du canal ou sur les parois (rétrécissement ou élargissement) permettrait de quantifier l'impact de la géométrie sur l'onde dans l'expérience.
Aujourd'hui, des modèles analogues permettent de mieux comprendre et d'anticiper les tsunamis. Si le phénomène de génération en lui-même (le plus souvent un séisme) ne peut être prédit, la détection de ces vagues a pu être améliorée grâce à des systèmes de balises et de bouées, permettant d'alerter les populations présentes sur les côtes. L'évacuation, si l'alerte a pu être donnée à temps, ou la présence d'abris en hauteur facilement accessibles, peuvent alors sauver des milliers de vies.
Bibliographie
| # | Référence | |
|---|---|---|
| [1] | G.B. Airy. Tides and Waves. Fellowes, 1845. | |
| [2] | S. Boury, H. Piot-Durand, L. Menou, R. Menu et J. Thibaut. Vagues solitaires : tsunamis en laboratoire. Bulletin de l'Union des Physiciens, 2020. | |
| [3] | G. Bouyrie. Arpenteur du web: physique des vagues. Bulletin de l'Union des Physiciens, 2015. | |
| [4] | C. Brouzet, P. Maurer et V. de Zotti. Fabriquons des tsunamis ! Culture sciences physiques, 2016. | |
| [5] | T. Dauxois et M. Peyrard. Physics of Solitons. Cambridge University Press, 2006. | |
| [6] | A. P. French. Vibrations and Waves. CBS Publishers and Editors, 2003. | |
| [7] | É. Guyon, J.-P. Hulin et L. Petit. Hydrodynamique physique, 3e éd. EDP sciences, 2012. | |
| [8] | A. Leroux. Mise en évidence de nouveaux types de vagues de très grandes amplitudes (thèse). 2013. | |
| [9] | M. Remoissenet. Waves Called Solitons. Springer, 1999. | |
Page adaptée de Boury et al., Vagues solitaires : tsunamis en laboratoire, article paru dans le Bulletin de l'Union des Physiciens [2].
CONTACT INFO
Email: sbry.phy@gmail.com
Office: Université Paris Cité Laboratory Matière et Systèmes Complexes (MSC) -- UMR 7057Bâtiment Condorcet -- Office 841A10 Rue Alice Domon et Léonie Duquet75013 Paris (France)
