Chapitre 3 Décrire le lien entre deux variables
3.1 Lien entre deux variables quantitatives
3.1.1 Description graphique
3.1.1.1 Nuage de points
On s’intéresse ici au jeu de données broceliande et au lien entre l’âge et la hauteur des arbres.
La représentation classique pour deux variables quantitatives et continues est une représentation par un nuage de points:
ggplot(broceliande, aes(x=age,y=hauteur))+
geom_point(col="khaki2")+
scale_x_log10()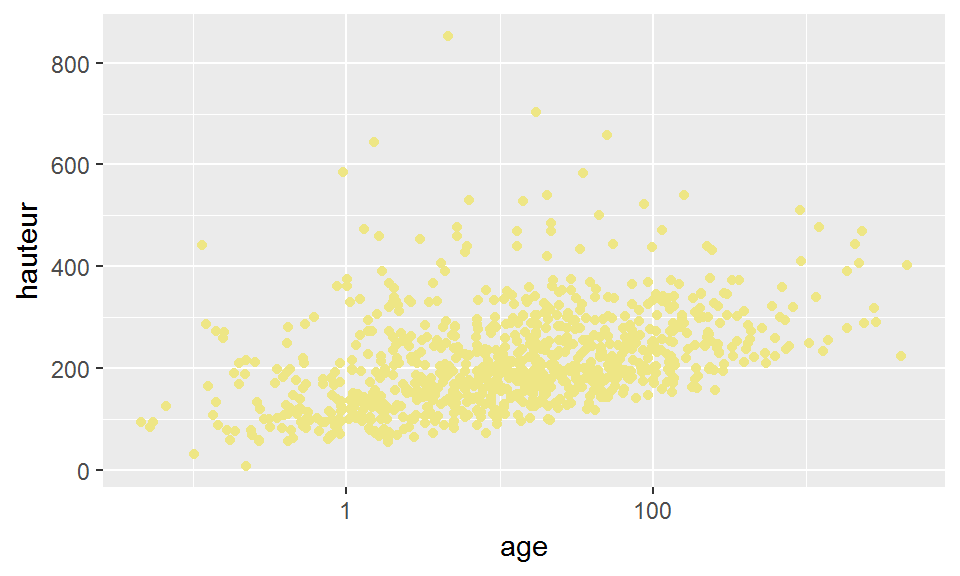
3.1.1.2 Droite/courbe de régression
Il est possible d’ajouter une droite ou une courbe pour décrire l’allure de la relation:
ggplot(broceliande, aes(x=age,y=hauteur))+
geom_point(col="khaki2")+
geom_smooth(span=0.25,col="khaki4")+
scale_x_log10()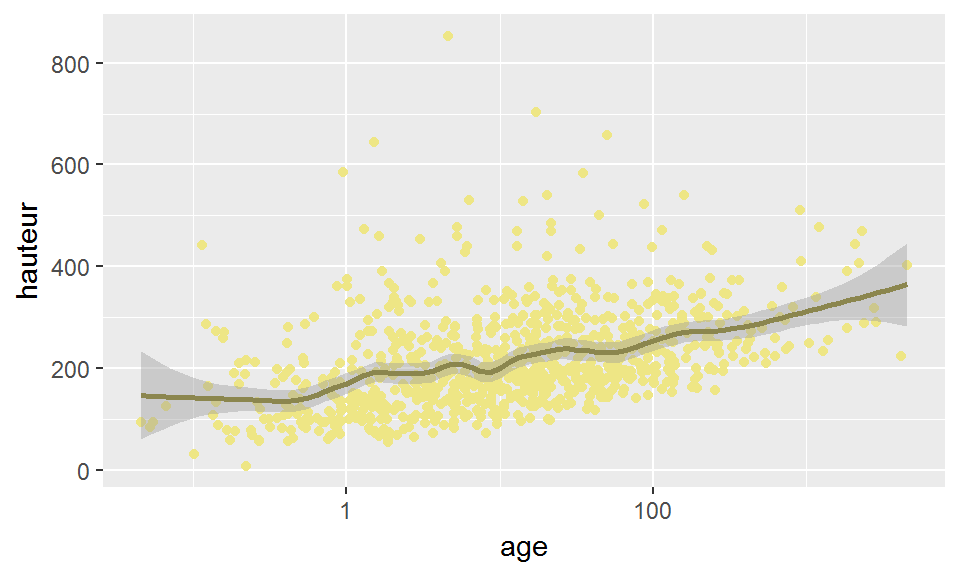
Par défaut, la courbe ajoutée par geom_smooth() est calculée par des méthodes non-paramétriques. Ici, par une régression loess.
Il est également possible de contraindre geom_smooth() à afficher une droite de régression linéaire:
ggplot(broceliande, aes(x=age, y=hauteur))+
geom_point(col="khaki2")+
geom_smooth(method="lm", col="khaki4")+
scale_x_log10()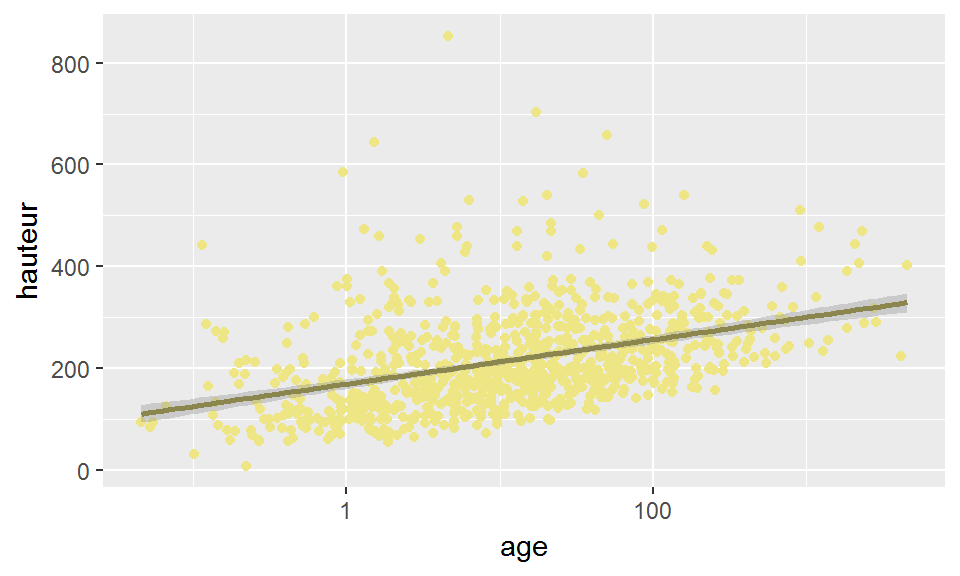
3.1.1.3 Variables quantitatives à valeurs discrètes
Lorsque les variables quantitatives sont à valeurs discrètes, et en fonction de leur distribution, il peut devenir nécessaire de “ruser” pour que la visualisation permette de se rendre compte qu’un point (x,y) correspond à \(n>1\) individus.
Par exemple, examinons le nombre de lutins vs le nombre de touffes de gui dans chaque arbre de notre jeu de données brocéliande.
Si l’on se contente d’un geom_point(), alors voilà ce qu’on observe:
ggplot(broceliande, aes(x=gui, y=lutins), col="orange")+
geom_point()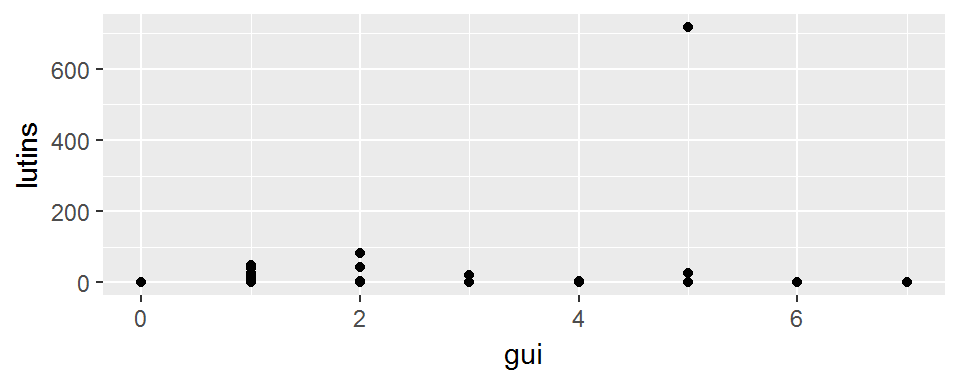
On n’a ici aucune idée de l’effectif réel observé pour chaque paire (x,y)…
On peut remédier à ce problème à l’aide d’un geom_jitter():
ggplot(broceliande, aes(x=gui, y=lutins))+
geom_jitter(col="orange")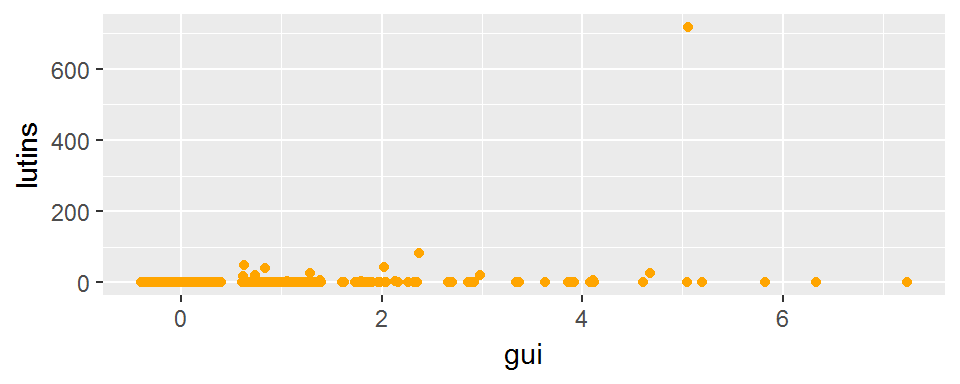
Il est également possible d’arranger le jeu de données pour donner un “poids” différent à chaque point en fonction de l’effectif:
broceliande_t=broceliande %>%
group_by(gui,lutins) %>%
summarise(n=n())
ggplot(broceliande_t, aes(x=gui,y=lutins))+
geom_point(aes(size=n), col="orange")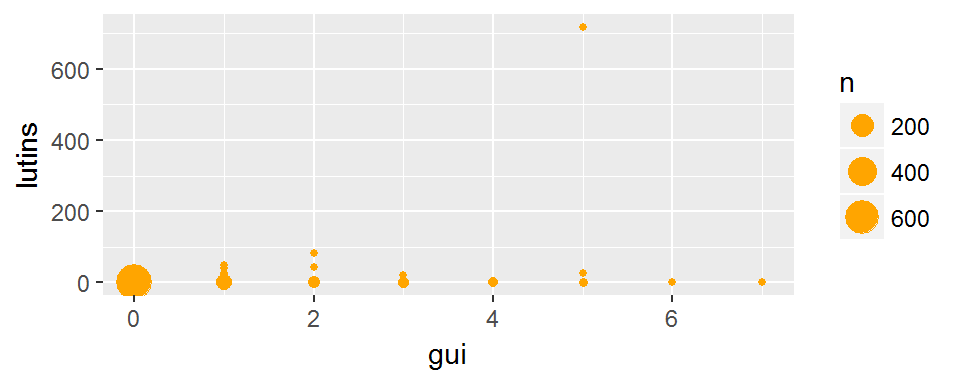
3.1.2 Description par le coefficient de corrélation
\[{Cor}(X,Y)= E\left[\frac{X-E(X)}{\sigma_X}\frac{Y-E(Y)}{\sigma_Y}\right]\]
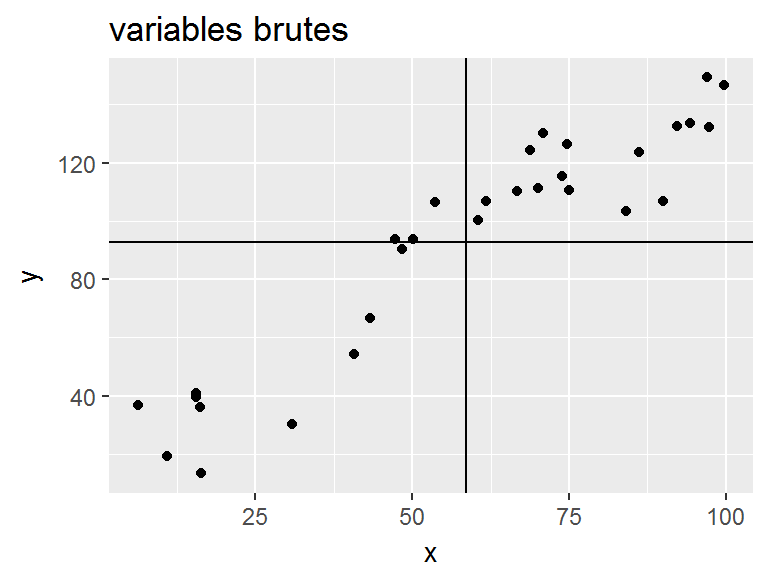
|
Ici les valeurs de \(X\) et \(Y\) |
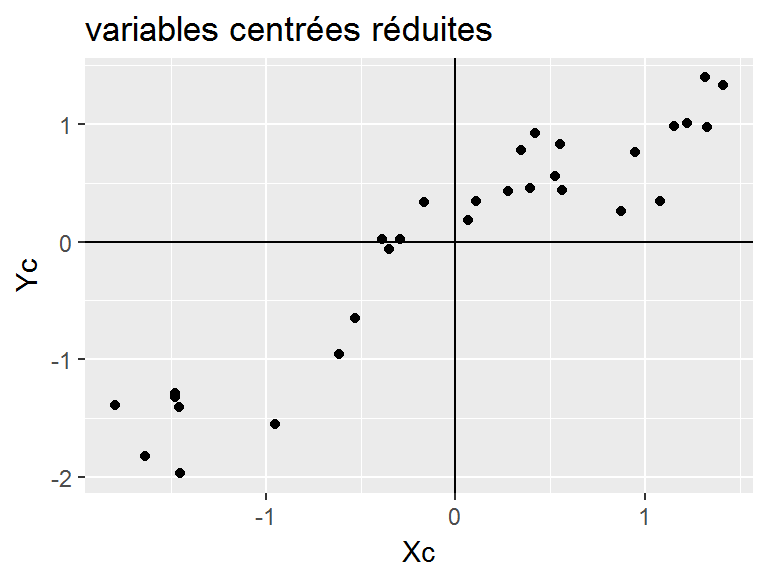
|
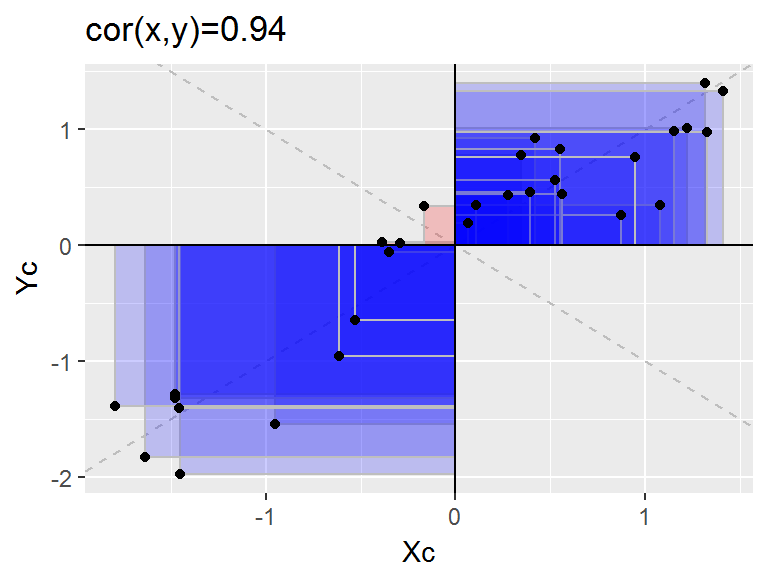
Ici les valeurs centrées réduites de \(X\) et \(Y\) soit en abscisse \(Xc=\frac{X-E(x)}{\sigma_X}\) et en ordonnée \(Yc=\frac{X-E(x)}{\sigma_X}\) |
|
Le coefficient de corrélation correspond à l’espérance du produit \(Xc.Yc\), soit la moyenne des “aires” (positives en bleu, négatives en rouge) |
3.1.2.1 Interprétation
Le coefficient de corrélation prend ses valeurs entre -1 et 1…
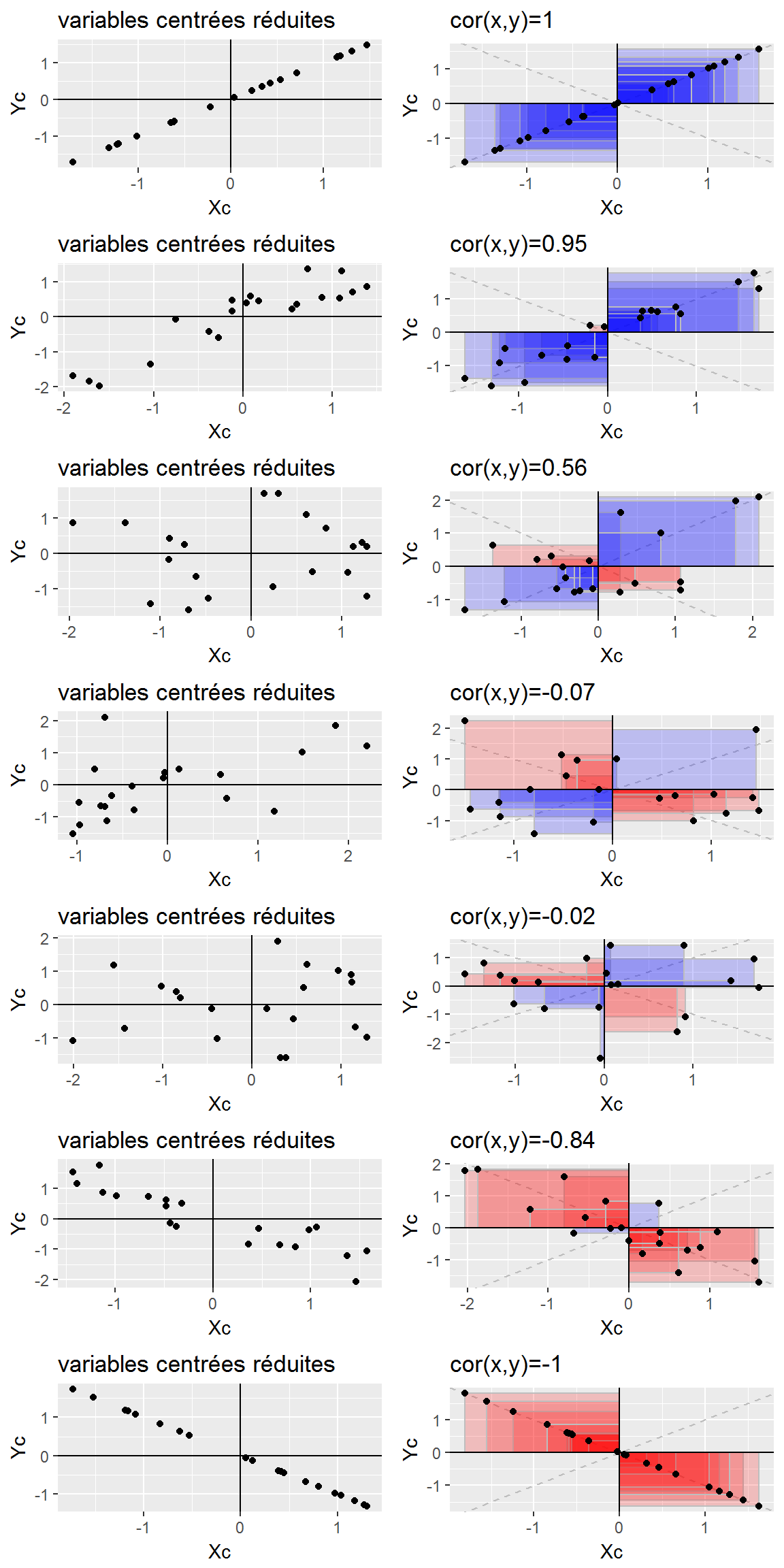
3.1.2.2 Calcul avec R
Pour calculer un coefficient de corrélation avec R, on utilise (tout simplement) la fonction cor():
cor(broceliande$age,broceliande$hauteur)## [1] 0.2246481cor(broceliande$hauteur,broceliande$largeur)## [1] 0.88091393.2 Lien entre une variable catégorielle et une variable quantitative
3.2.1 Description graphique
Le type de graphique sans doute le plus souvent employé pour montrer la relation entre une variable catégorielle et une variable quantitative est la boîte à moustaches ou boxplot.
Intéressons-nous par exemple au lien entre enchantement et perlimpinpin dans le jeu de données brocéliande:
ggplot(broceliande, aes(x=enchantement, y=perlimpinpin))+
geom_boxplot(fill="lightblue")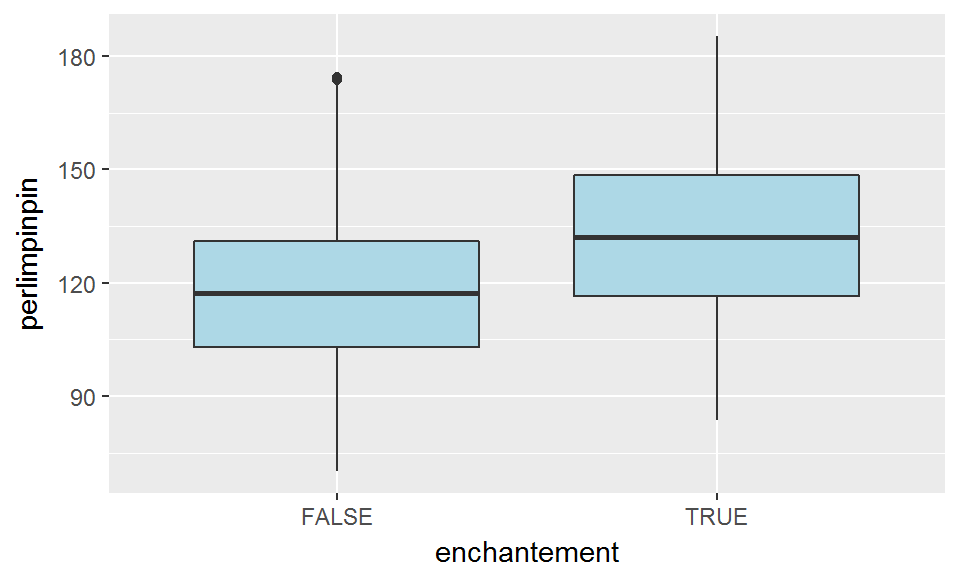
Si la variable quantitative est à valeurs discrètes et/ou a une très lourde queue de distribution, alors il peut arriver que représenter la distribution par une boîte à moustaches soit peu pertinent. Par exemple, représenter la relation entre espece et lutins ne semble pas être une très bonne idée (et une transformation des données n’y changerait rien…):
ggplot(broceliande, aes(x=espece, y=lutins))+
geom_boxplot(col="orange")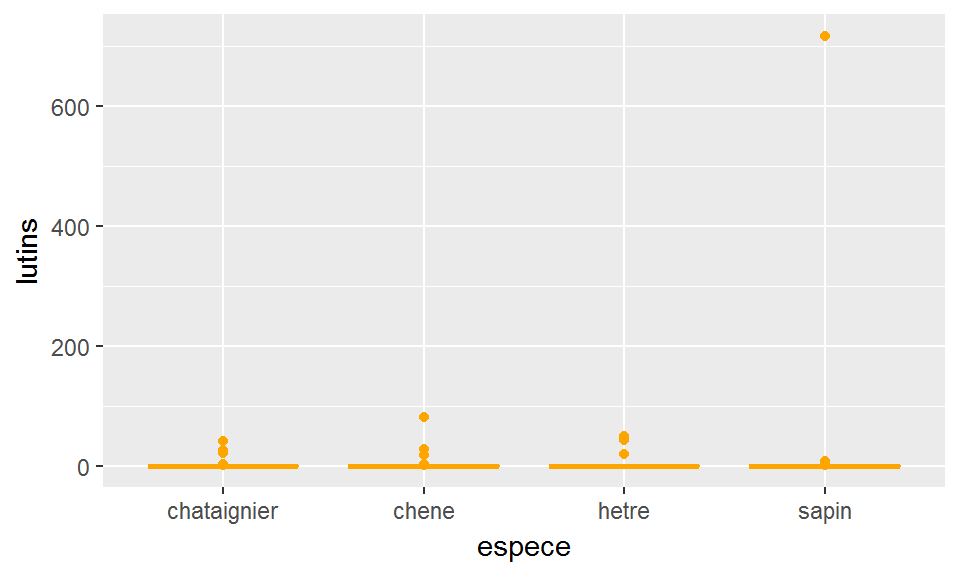
ggplot(broceliande,aes(x=lutins))+
geom_histogram(fill="orange",bins=10)+
facet_grid(espece~.)+
scale_y_sqrt()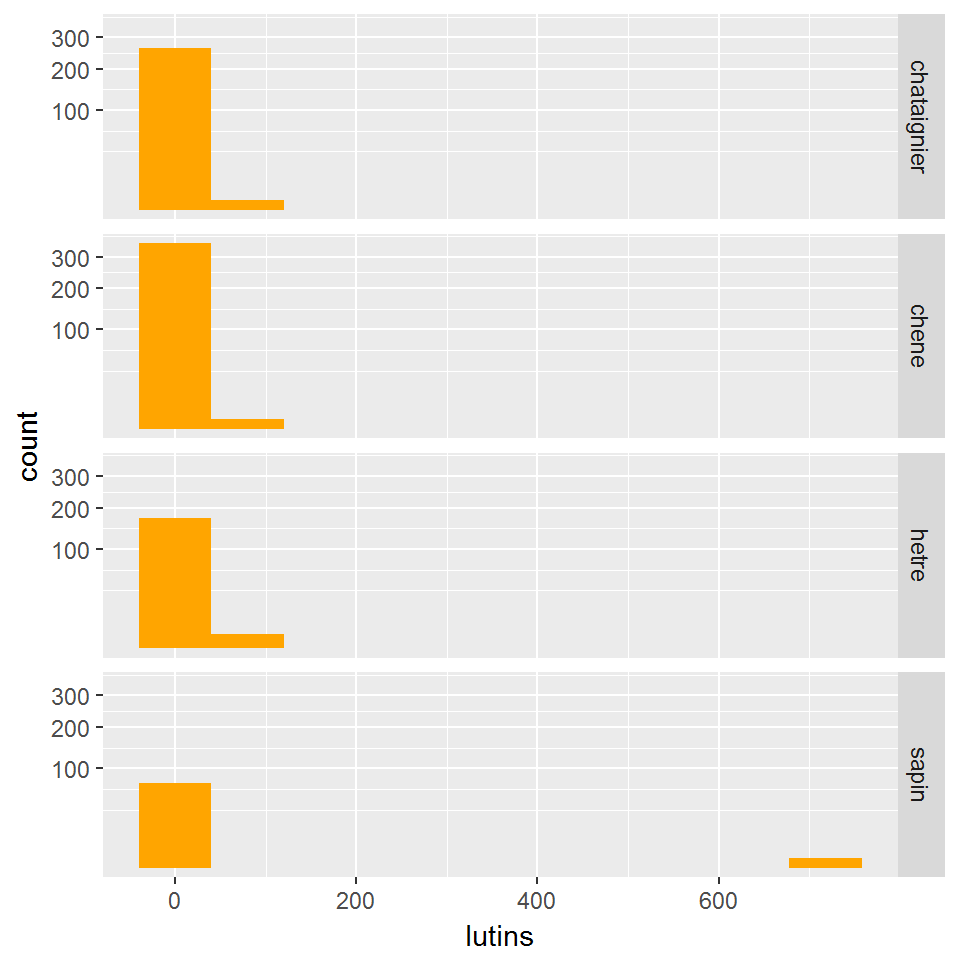
3.2.2 Description par une métrique
Pour décrire le lien entre une variable catégorielle et une variable quantitative, on peut calculer certaines caractéristiques de la variable quantitative (par exemple sa moyenne) par groupe (défini par les modalités de la variable catégorielle). Pour cela, la fonction summarise() du package dplyr est tout indiquée:
broceliande %>%
group_by(espece) %>%
summarise(moy_largeur=mean(largeur),
max_largeur=max(largeur),
min_largeur=min(largeur),
sd_largeur=sd(largeur))## # A tibble: 4 x 5
## espece moy_largeur max_largeur min_largeur sd_largeur
## <fct> <dbl> <dbl> <dbl> <dbl>
## 1 chataignier 215 713 28.8 107
## 2 chene 259 793 9.09 124
## 3 hetre 211 680 42.1 106
## 4 sapin 171 416 49.2 84.0Considérez le jeu de données potions et calculez les coefficients de corrélation entre
p_conjurationetp_destructionp_alterationetp_destruction
Au vu de ces résultats (et sans prendre en compte tous les paramètres complexes qui président à l’élaboration d’une potion magique), semble-t-il a priori plus facile de concevoir une potion qui fasse apparaître un dragon cracheur de feu (conjuration + destruction) ou une potion qui vous transforme en dragon cracheur de feu (alteration + destruction) ?
3.3 Lien entre deux variables catégorielles

|
On reprend ici le jeu de données chateauxEtBoulots et on va s’intéresser ici, plus particulièrement, au lien entre l’activité des personnages et leur sexe.
|
3.3.1 Description graphique
On peut produire des barplots qui dépendent d’une des variables en x, et de l’autre par la couleur de remplissage par exemple.
ggplot(chateauxEtBoulots,aes(x=activite))+
geom_bar(aes(fill=sexe))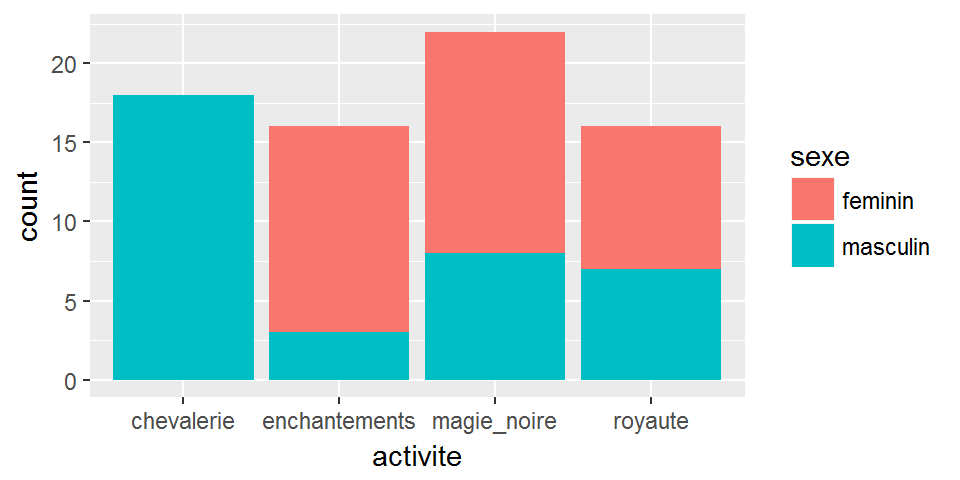
Plusieurs positionnements pour les modalités du facteur sont possibles. Le postionnement “fill” permet une meilleure visualisation des proportions de sexe dans chaque modalité de activite.
ggplot(chateauxEtBoulots,aes(x=activite))+
geom_bar(aes(fill=sexe),position="fill")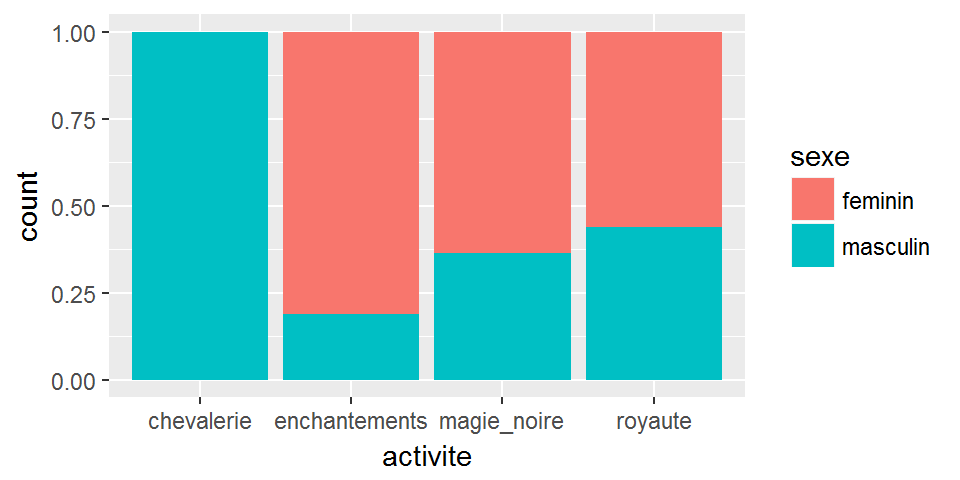
3.3.2 Tableau de contingences
L’établissement d’un lien entre deux variables catégorielles passe en premier lieu par le calcul du tableau de contingences qui donne les effectifs observés pour toutes les associations possibles de modalités.
table(chateauxEtBoulots$activite,chateauxEtBoulots$sexe)##
## feminin masculin
## chevalerie 0 18
## enchantements 13 3
## magie_noire 14 8
## royaute 9 7La lecture de ce tableau suggère que la chevalerie est associée aux hommes (pas une seule “chevalière” dans notre jeu de données), tandis que la magie semble plutôt associée aux femmes (plus de fées et sorcières que d’enchanteurs et de mages noirs). Princes et princesses semblent en revanche être autant représentés les uns que les autres.
L’usage du package janitor permet une petite mise en forme de cette table:
library(janitor)
chateauxEtBoulots %>%
tabyl(activite,sexe) %>%
adorn_totals("row") %>% # Rajoute la ligne "Total"
adorn_totals("col") %>% # Rajoute la colonne "Total"
adorn_percentages(denominator="all") %>% # Transforme les effectifs en pourcentages
adorn_pct_formatting(digits=1) # Limite le nombre de digits affichés ## activite feminin masculin Total
## chevalerie 0.0% 25.0% 25.0%
## enchantements 18.1% 4.2% 22.2%
## magie_noire 19.4% 11.1% 30.6%
## royaute 12.5% 9.7% 22.2%
## Total 50.0% 50.0% 100.0%Considérez le tableau chateauxEtBoulots et les variables tenue et region. La couleur rose semble particulièrement peu en vogue dans une des trois régions de Fantaisie. Laquelle est-ce?