Chapitre 5 Modéliser le lien entre deux variables

Maintenant que nous avons abordé la logique “générale” du test d’hypothèse, intéressons-nous plus particulièrement à deux modèles (ceux de la régression linéaire et de l’ANOVA -ou analyse de variance-).

Un modèle est un outil qui peut être utile pour simplifier une problématique et formaliser une question. Dans le cas des modèles statistiques que nous allons aborder dans ce chapitre, la formalisation de cette question permet d’appliquer et interpréter un test d’hypothèse selon la même logique que celle expliquée auparavant dans la section 4.

Un modèle décrivant une variable \(Y\) en fonction d’une autre variable \(X\) s’accompagne typiquement des questions suivantes:

En termes d’effet: quel est l’effet de \(X\) sur \(Y\) ?
En termes de significativité: Est-ce que l’effet observé de \(X\) sur \(Y\) est significatif, ou au contraire pourrait-il simplement s’expliquer par le hasard d’échantillonnage? C’est à cette question que le test d’hypothèse est censé apporter une réponse.
En termes de prédiction et de qualité d’ajustement: Serait-on en mesure de prédire la valeur de \(Y\), connaissant celle de \(X\), avec précision? \(Y\) est-elle “étroitement” liée à \(X\) ou juste “vaguement”?). Autrement dit, la variabilité résiduelle des observations par rapport au modèle proposé est-elle forte?

Réaliser une régression linéaire ou une ANOVA va nous permettre de répondre à ces questions, en nous fournissant notamment les éléments de réponse suivants:

l’effet (signe de l’effet et taille d’effet), indicateur du sens et de l’ampleur de l’influence de la variable explicative sur la variable réponse. Dans notre exemple, \(Y\) augmente quand \(X\) augmente: l’effet de \(X\) sur \(Y\) est positif
la p-value, indicatrice de la significativité de l’effet
le R\(^2\), ou coefficient de détermination, indicateur de la qualité prédictive et de la qualité d’ajustement du modèle

5.1 La régression linéaire: lien entre deux variables quantitatives

5.1.1 Modèle

Un modèle de régression linéaire peut être écrit comme suit:

\[Y=\alpha X+\beta+E(0,\sigma^2)\]

où

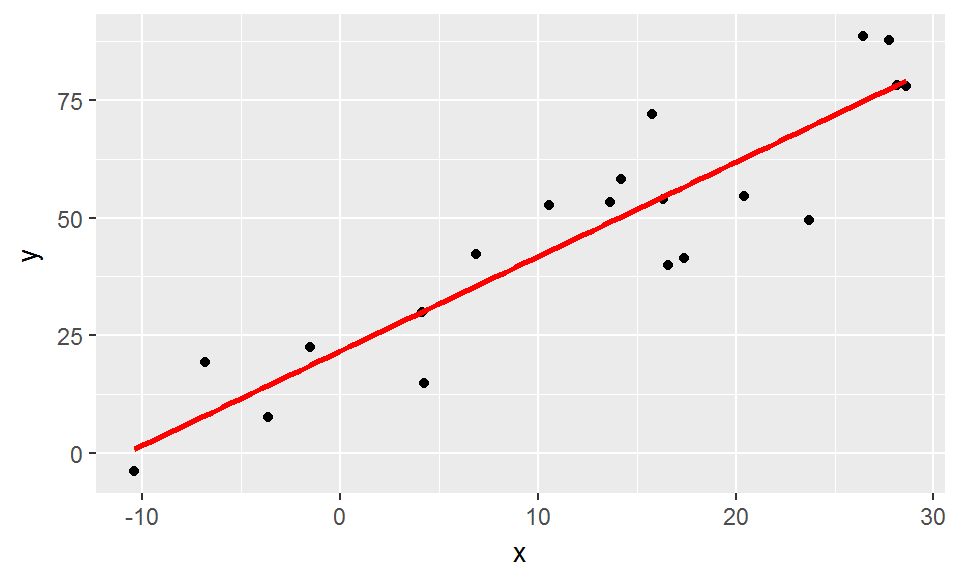
\(\alpha\) correspond à la pente de régression (ici \(\approx\) 2)
\(\beta\) correspond à l’ordonnée à l’origine (ici \(\approx\) 20)
\(E(0,\sigma^2)\) correspond à une erreur dont on considèrera (pour le moment) qu’elle suit une loi normale de moyenne nulle et de variance \(\sigma^2\) Cette erreur rend compte des écarts entre les points et le modèle (la droite) (ici \(\sigma\approx\) 10, c’est-à-dire que 95% de écarts sont dans l’intervalle \(\approx\)[-20,20]).

Ce modèle est un modèle linéaire car la variable \(Y\) s’écrit comme une “combinaison linéaire” de la variable \(X\).

5.1.2 La régression linéaire, en théorie

5.1.2.1 Ajustement

	On considère deux variables quantitatives \(X\) et \(Y\)
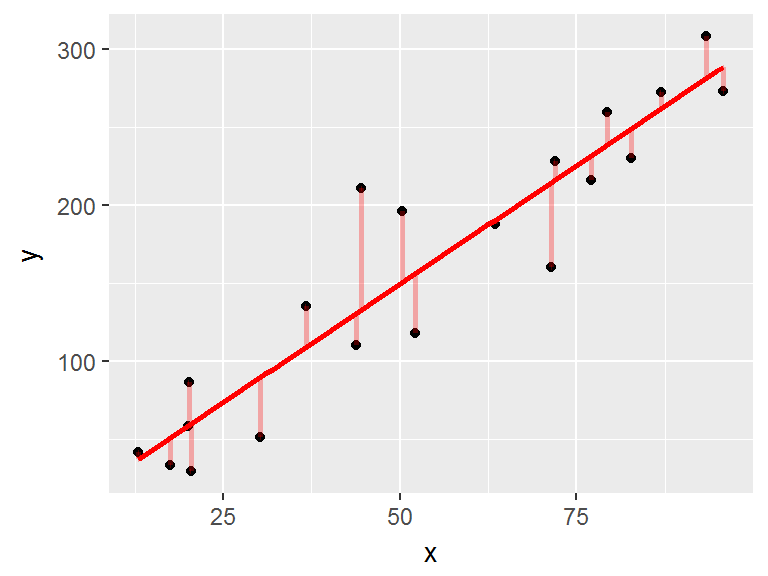
	La droite de régression est celle qui minimise la somme des carrés des résidus (SCR): les résidus sont les écarts (en rouge) entre les points et la droite de régression

5.1.2.2 R2

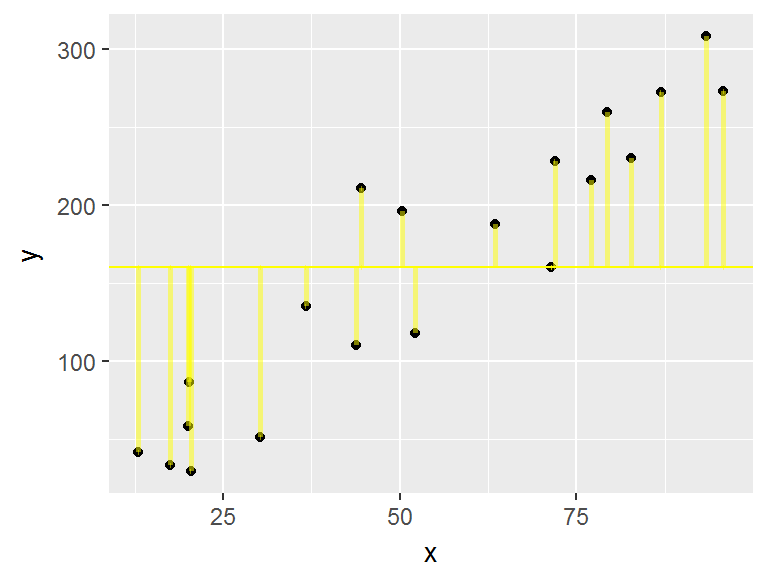
le \(R^2\) correspond à la part de variabilité de \(Y\) qui est expliquée par le modèle.

\[R^2=\frac{SCT-SCR}{SCT}=1-\frac{SCR}{SCT}\] où

SCR est la somme des carrés des résidus, c’est à dire la somme des distances des points au modèle (ici représentées en rouge) au carré
SCT est la somme des carrés totale i.e. la somme des distances à la moyenne de Y (ici représentées en jaune), au carré

Le \(R^2\) varie entre 0 et 1.

Ici, il vaut 0.93.

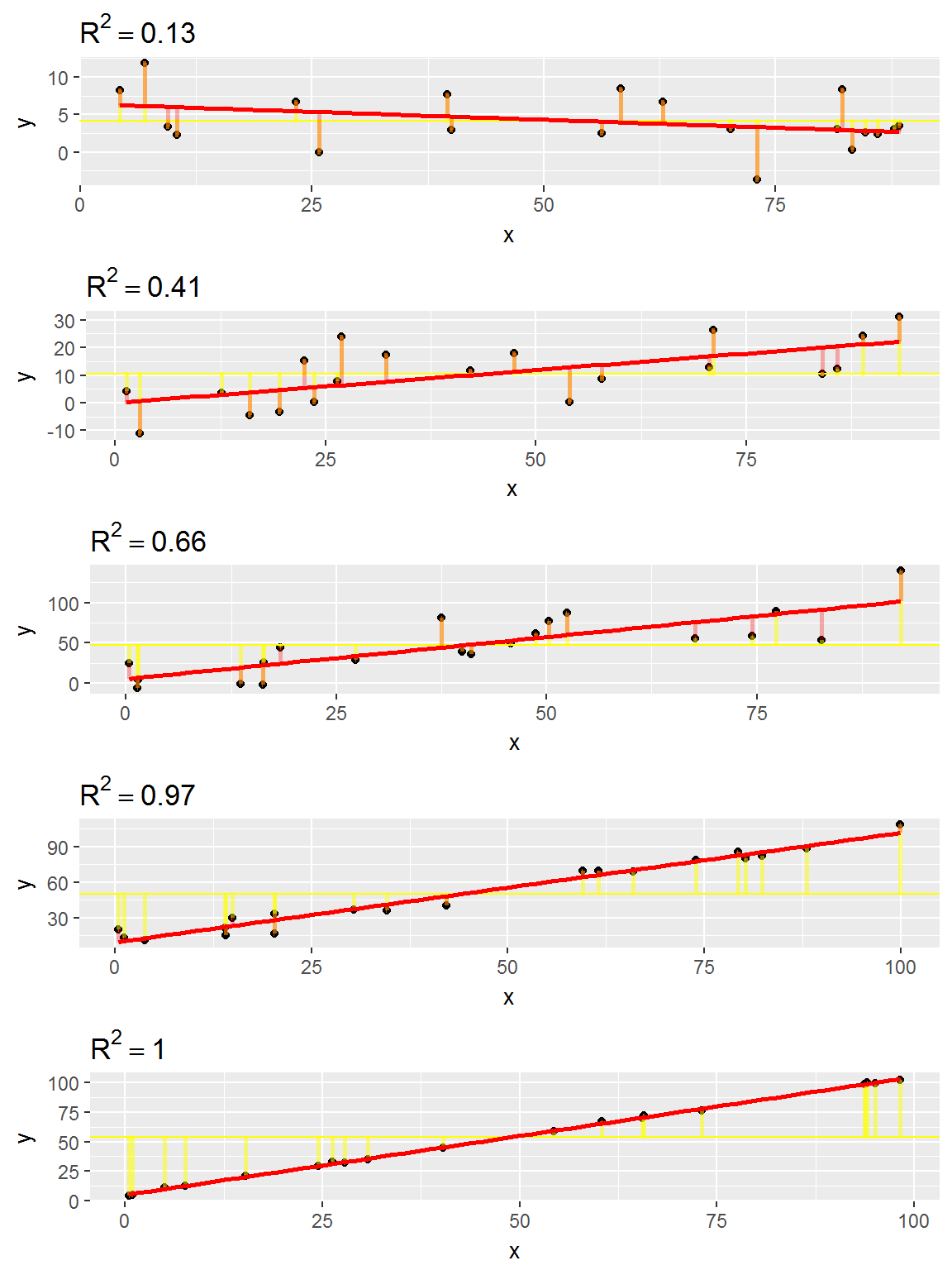
Plus le \(R^2\) est proche de 1, plus la part de variabilité de \(Y\) expliquée par le modèle (donc, ici, expliquée par \(X\)) est importante.

Le \(R^2\) constitue une mesure de la qualité prédictive d’un modèle: à partir d’une valeur de \(X\), est-on capable de prédire la valeur de \(Y\) sans trop se tromper? Si le \(R^2\) est proche de 1, alors vraisemblablement, c’est le cas…

5.1.2.3 Test(s) associé au modèle

Les tests d’hypothèse associés à un modèle de régression portent sur la valeur des coefficients (notamment valeur de la pente \(\alpha\)).

On s’intéresse ainsi à:

l’hypothèse \(\alpha=0\), qui si elle est vérifiée correspond à une situation où \(X\) n’a pas d’effet sur \(Y\)
plus rarement (parce que la valeur de \(Y\) pour \(X=0\) a rarement d’intérêt), on peut s’intéresser à l’hypothèse \(\beta=0\)

Le test de Student réalisé dans le cadre d’une régression linéaire correspond ainsi à un test d’une hypothèse nulle du type H\(_0=\){le paramètre estimé est nul}.

Une p-value faible (conventionnellement, inférieure à 5%) entraîne un rejet de l’hypothèse nulle, auquel cas on conclut que \(X\) a un effet significatif sur \(Y\).

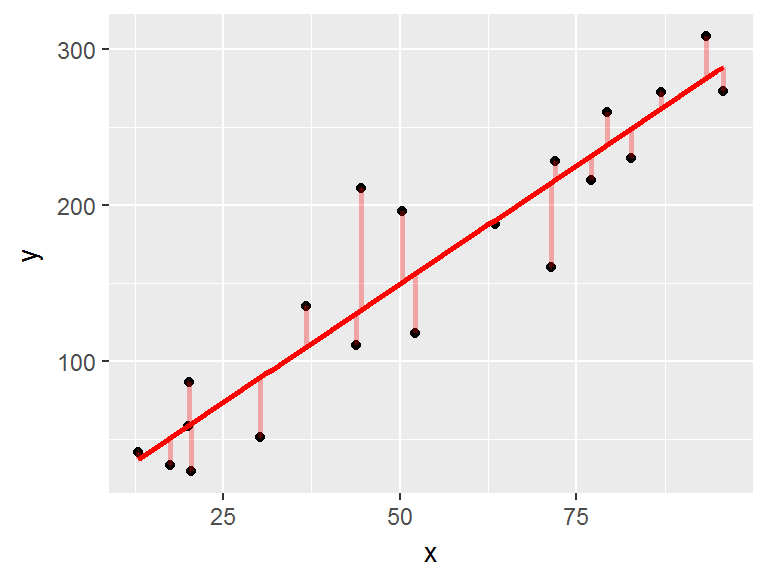
Exemples de relations entre deux variables X et Y (toutes deux quantitatives). On a fait varier ici 3 éléments: la taille d’effet, la variabilité résiduelle, et la taille d’échantillon.

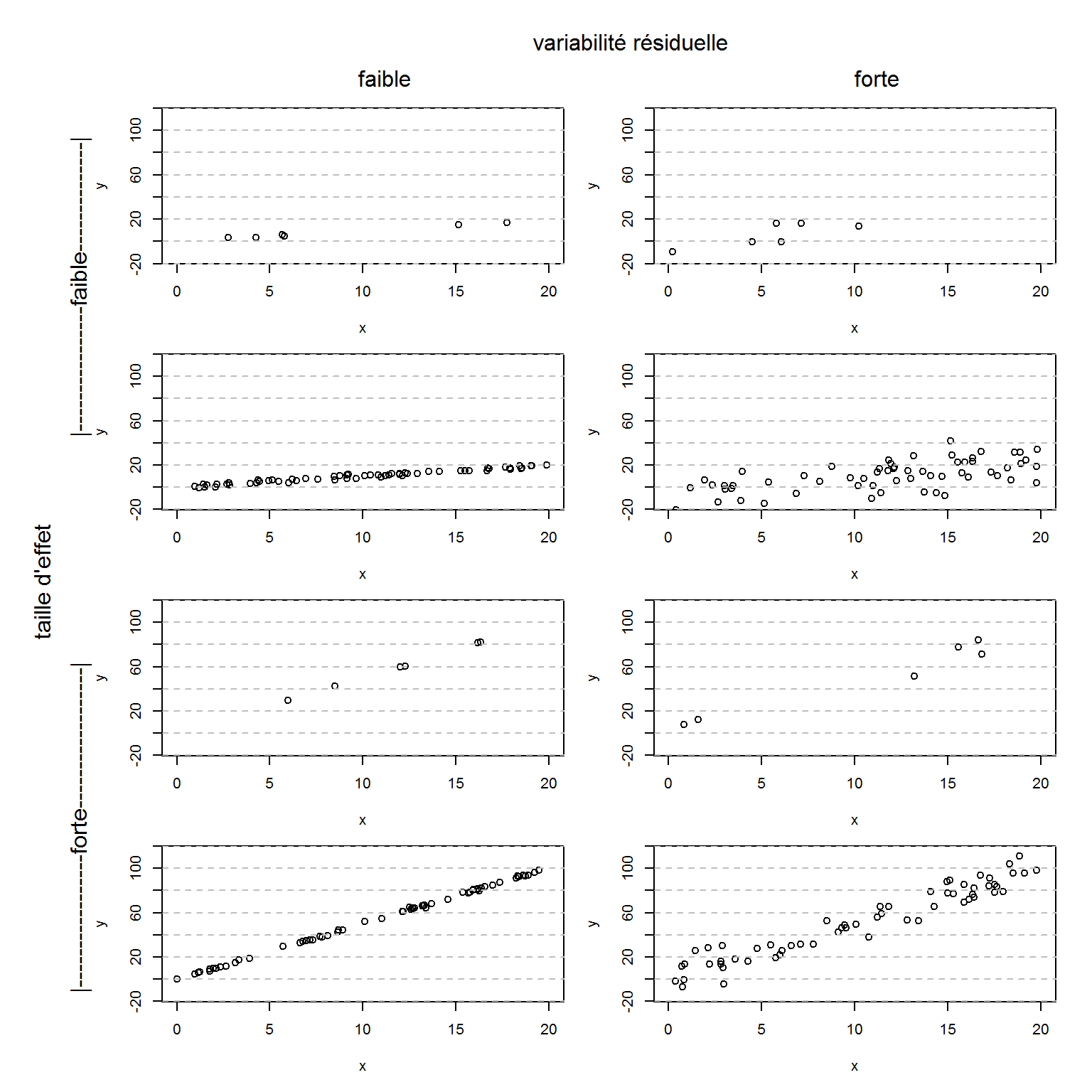
5.1.3 La régression linéaire, en pratique

Considérons le jeu de données brocéliande et intéressons-nous au lien entre hauteur et perlimpinpin:

ggplot(broceliande, aes(x=hauteur, y=perlimpinpin))+
  geom_point(col="lightblue")+
  geom_smooth(method="lm")

Ici on a un nombre de données important ET une allure des résidus qui se rapproche des conditions d’application du test d’hypothèse (normalité, homoscedasticité).

Pour réaliser le modèle de régression linéaire, on utilise la fonction lm() (comme linear model). Les variables hauteur et perlimpinpin correspondant à des vecteurs numériques, le type de modèle linéaire ajusté est une régression linéaire.

mylm=lm(perlimpinpin~hauteur, data=broceliande)
mylm

## 
## Call:
## lm(formula = perlimpinpin ~ hauteur, data = broceliande)
## 
## Coefficients:
## (Intercept)      hauteur  
##   109.26873      0.05083

L’affichage de l’objet mylm montre notamment les valeurs estimées de \(\alpha\) et \(\beta\):

\(\hat\alpha\)= 0.0508296

\(\hat\beta\)= 109.2687323

Pour voir d’autres éléments (comme les résultats des tests d’hypothèse et le \(R^2\)) on peut utiliser la fonction summary()

mysummary=summary(lm(perlimpinpin~hauteur, data=broceliande))
mysummary

## 
## Call:
## lm(formula = perlimpinpin ~ hauteur, data = broceliande)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -48.860 -14.941  -0.297  14.114  66.766 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 1.093e+02  1.744e+00  62.650  < 2e-16 ***
## hauteur     5.083e-02  7.355e-03   6.911 9.34e-12 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 21.16 on 862 degrees of freedom
## Multiple R-squared:  0.0525, Adjusted R-squared:  0.0514 
## F-statistic: 47.77 on 1 and 862 DF,  p-value: 9.336e-12

Les éléments renvoyés par summary(reg) correspondent bien à

l’évaluation de l’effet (estimation du paramètre \(\alpha\)),
la significativité de l’effet (p-value) évaluée à travers un test de Student,
la qualité d’ajustement décrite par le R\(^2\).

Dans notre cas, on a:

une valeur de pente estimée à 0.051, c’est-à-dire que la hauteur de l’arbre a un léger effet positif sur la quantité de perlimpinpin qu’on y trouve
un effet significatif au seuil de 5% (p-value=0, c’est-à-dire que l’effet positif observé n’est pas simplement lié à l’aléa d’échantillonnage mais est bien le reflet d’un effet réel
un R\(^2\) de 0.053, c’est-à-dire que la qualité d’ajustement est très faible (on ne peut pas prédire précisément la quantité de poudre de perlimpinpin dans un arbre en se basant sur sa hauteur)

Pour récupérer chacun de ces éléments, on peut procéder comme suit:

mylm$coeff # estimation des paramètres

##  (Intercept)      hauteur 
## 109.26873234   0.05082956

mylm$coeff[2] # estimation du paramètre de pente

##    hauteur 
## 0.05082956

summary(mylm)$coeff[2,4] # p-value associée à l'hypothèse pente=0

## [1] 9.335863e-12

summary(mylm)$r.squared # valeur du R2

## [1] 0.05250411

Considérez le jeu de données potions et examinez la relation entre

la variable i_givreboises et la variable p_invisibilite.
la variable i_ectoplasme et la variable p_invisibilite
la variable i_larmes_crocodile et la variable p_invisibilite

Dans chacun de ces cas, que pouvez-vous dire sur - le signe et la taille de l’effet? - la significativité de l’effet? - la performance de prédiction?

5.2 L’ANOVA: lien entre une variable catégorielle et une variable quantitative

5.2.1 Modèle

Un modèle d’ANOVA à 1 facteur (facteur \(X\) à \(J\) modalités \(m_1\), \(m_2\), …., \(m_J\)) peut être écrit comme suit:

\[ Y=\nu_1I_{X=m_1}+ \nu_2I_{X=m_2}+...+ \nu_JI_{X=m_J}+E(0,\sigma^2) \] où

\(I_{X=m_i}\) est la variable indicatrice de l’événement \(X=m_i\) (cette variable vaut 1 dans le cas où \(X=m_i\), 0 autrement)
\(\nu_i\) correspond à la valeur attendue pour \(Y\) pour \(X=m_i\)
\(E(0,\sigma^2)\) correspond à une erreur dont on considèrera (pour le moment) qu’elle suit une loi normale de moyenne nulle et de variance \(\sigma^2\) Cette erreur rend compte des écarts entre les points et le modèle (la droite) (ici \(\sigma\approx\) 10, c’est-à-dire que 95% de écarts sont dans l’intervalle \(\approx\)[-20,20]).

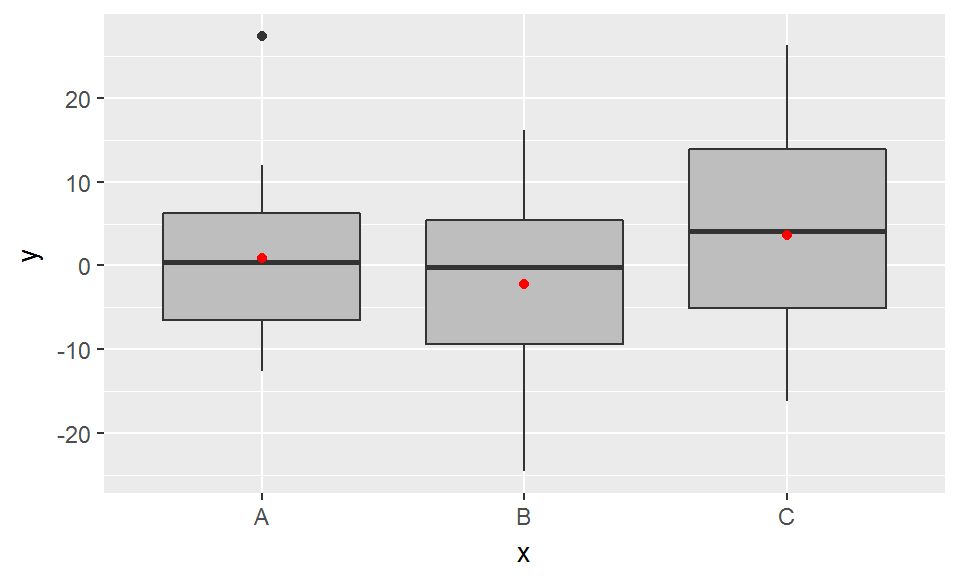
Là où le t-test permettait de tester des différences de moyennes entre deux groupes seulement, l’ANOVA permet de considérer un nombre de groupes J>2.

5.2.2 L’ANOVA, en théorie

5.2.2.1 Ajustement

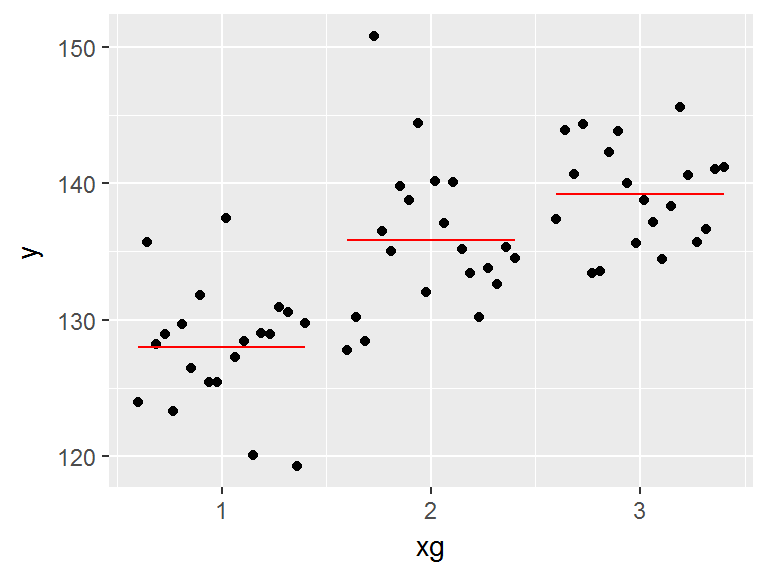
	On considère deux variables: \(X\) (catégorielle) et \(Y\) (quantitative)
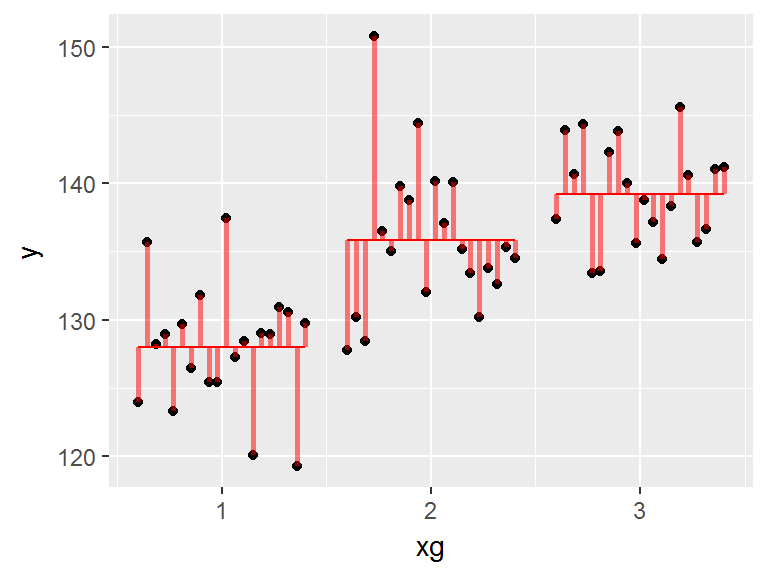
	Le modèle est celui qui minimise la somme des carrés des résidus (SCR): les résidus sont les écarts (en rouge) entre les points et le modèle

5.2.2.2 R2

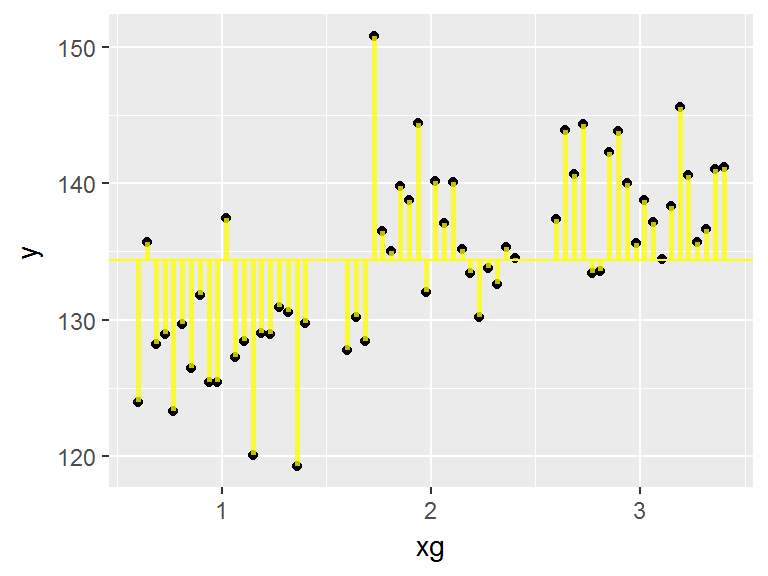
le \(R^2\) correspond à la part de variabilité de \(Y\) qui est expliquée par le modèle.

\[R^2=\frac{SCT-SCR}{SCT}=1-\frac{SCR}{SCT}\] où

SCR est la somme des carrés des résidus, c’est à dire la somme des distances des points au modèle (ici représentées en rouge) au carré
SCT est la somme des carrés totale i.e. la somme des distances à la moyenne de Y (ici représentées en jaune), au carré

Le \(R^2\) varie entre 0 et 1.

Ici, il vaut 0.59.

Plus le \(R^2\) est proche de 1, plus la part de variabilité de \(Y\) expliquée par le modèle (donc, ici, expliquée par \(X\)) est importante.

5.2.2.3 Test associé à une ANOVA

Le test associé à une ANOVA est un test de Fisher (ou test F).

Le test F permet de répondre à la question “la variable \(X\) a-t-elle un effet sur \(Y\)?”

Soit l’hypothèse H\(_0\), selon laquelle “la variable \(X\) n’a pas d’effet sur \(Y\)”. Sous cette hypothèse Y est distribué autour d’une valeur moyenne globale.

Soit la statistique F:

\[ \frac{\left(\frac{SC_0-SC_1}{ddl_0-ddl_1}\right)}{\left(\frac{SC_1}{ddl_1}\right)} \]

où

SC\(_0\)=somme des carrés des écarts au modèle 0 = SCT
SC\(_1\)=somme des carrés des écarts au modèle 1 = SCR
ddl\(_0\)=nombre de degrés de liberté du modèle 0
ddl\(_1\)=nombre de degrés de liberté du modèle 1

Supposons que l’hypothèse H\(_0\) est vraie.

Dans ce cas, \(F\) suit une distribution F avec (ddl\(_0\)-ddl\(_1\), ddl\(_0\)) degrés de liberté, et on peut calculer la probabilité d’observer la valeur obtenue pour la statistique F (i.e. la p-value).

Si cette p-value est faible, cela signifie que ce qu’on observe est peu vraisemblable sous l’hypothèse que l’on a faite au départ, l’on rejette donc cette hypothèse.

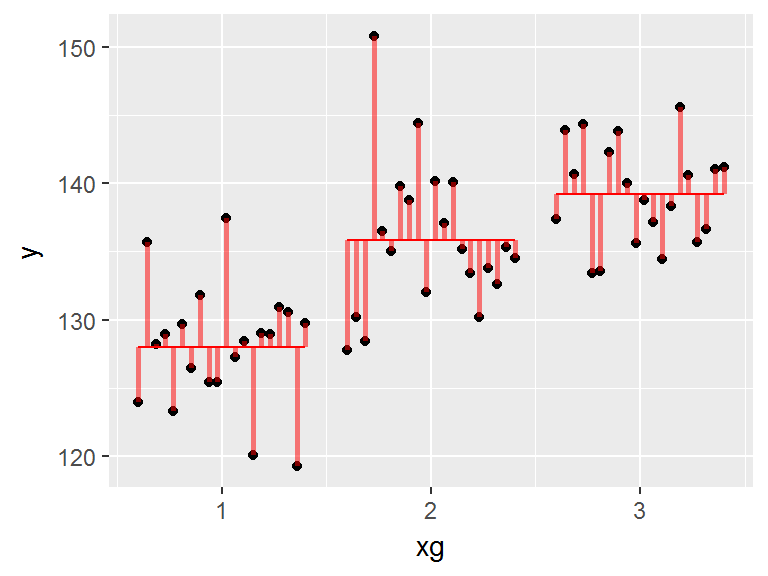
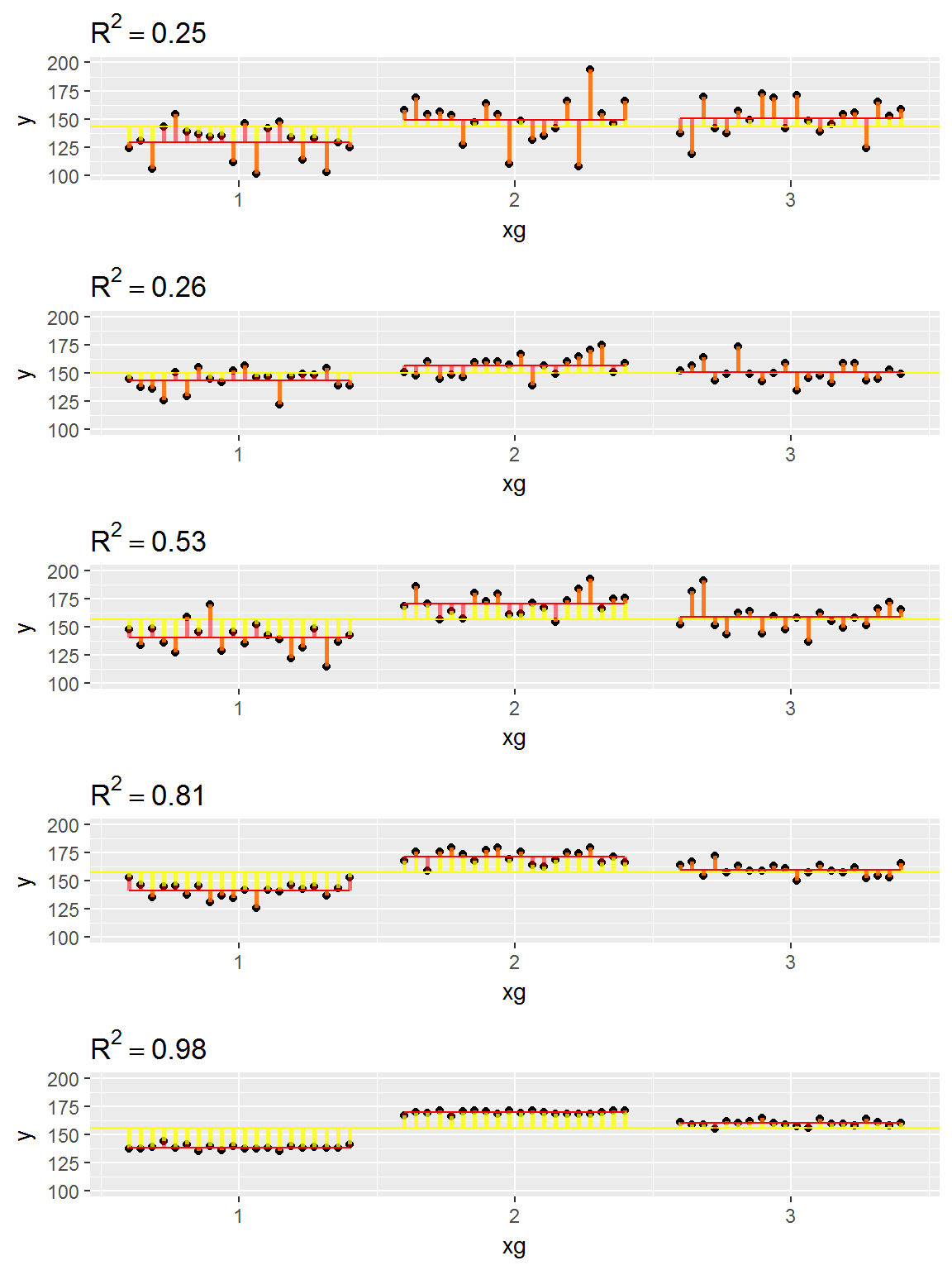
Exemples de relations entre les variables X (qualitative) et Y (quantitative). On a fait varier ici 3 éléments: la taille d’effet, la variabilité résiduelle, et la taille d’échantillon.

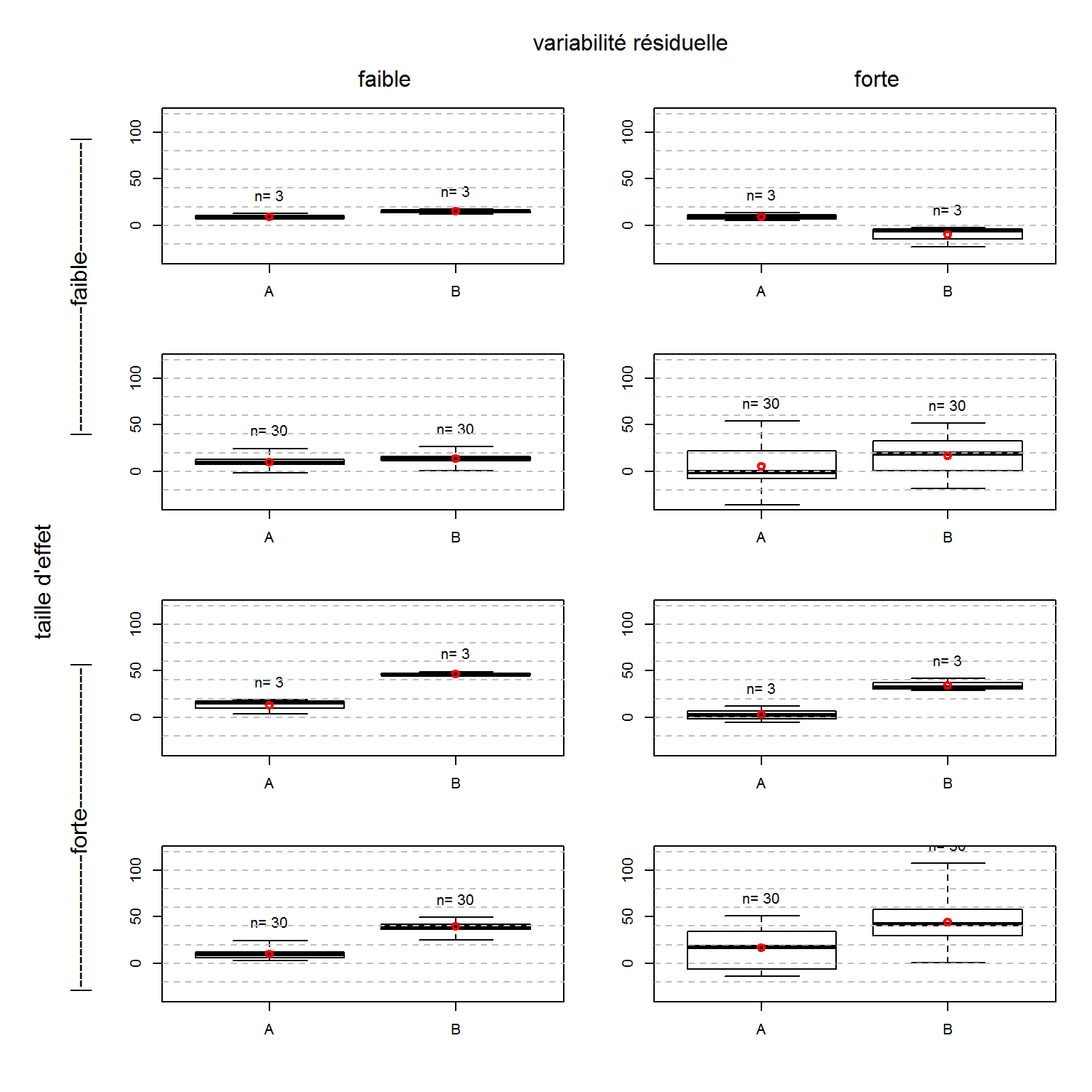
5.2.3 L’ANOVA, en pratique

On s’intéresse par exemple aux données de la table broceliande, et on analyse l’influence de \(X\)=espece sur \(Y\)=perlimpinpin. On cherche ainsi à identifier s’il existe des différences de moyenne de \(Y\) en fonction des groupes définis par \(X\).

5.2.3.1 Représentation et ajustement du modèle

broc_esp_perl_resume=broceliande %>% 
  group_by(espece) %>% 
  summarise(moy_perlimpinpin=mean(perlimpinpin))
ggplot(broceliande, aes(x=espece, y=perlimpinpin))+
         geom_boxplot(col="lightblue")+
  geom_point(data=broc_esp_perl_resume, aes(y=moy_perlimpinpin), col="blue")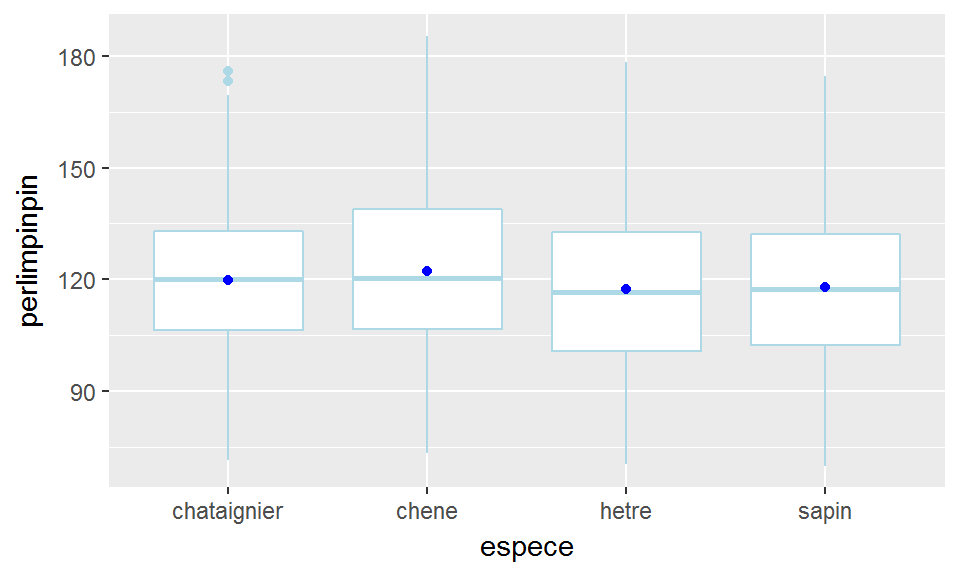

Pour réaliser une ANOVA, on va commencer par ajuster un modèle linéaire (comme dans le cas d’une régression linéaire).

mylm_rel=lm(perlimpinpin~espece, data=broceliande)
mylm_rel

## 
## Call:
## lm(formula = perlimpinpin ~ espece, data = broceliande)
## 
## Coefficients:
## (Intercept)  especechene  especehetre  especesapin  
##     119.891        2.468       -2.412       -1.868

mylm_abs=lm(perlimpinpin~espece+0, data=broceliande)
mylm_abs

## 
## Call:
## lm(formula = perlimpinpin ~ espece + 0, data = broceliande)
## 
## Coefficients:
## especechataignier        especechene        especehetre  
##             119.9              122.4              117.5  
##       especesapin  
##             118.0

Examinez la différence entre les deux modèles: en utilisant la première formule les moyennes sont évaluées relativement à un niveau de référence (en l’occurence, le premier): les éléments renvoyés par lm1 répondent donc à la question “les moyennes par groupe sont-elles significativement différentes de celle du premier groupe?”. Dans le deuxième cas, les moyennes par groupe sont évaluées de manière absolue. C’est plutôt dans cette deuxième conception qu’on se place ici (car les chataigniers ne constituent pas une sorte de groupe “témoin”):

summary(mylm_abs)

## 
## Call:
## lm(formula = perlimpinpin ~ espece + 0, data = broceliande)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -49.07 -15.39  -0.65  14.34  63.05 
## 
## Coefficients:
##                   Estimate Std. Error t value Pr(>|t|)    
## especechataignier  119.891      1.332   90.04   <2e-16 ***
## especechene        122.359      1.157  105.76   <2e-16 ***
## especehetre        117.479      1.643   71.49   <2e-16 ***
## especesapin        118.023      2.520   46.84   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 21.68 on 860 degrees of freedom
## Multiple R-squared:  0.9687, Adjusted R-squared:  0.9685 
## F-statistic:  6649 on 4 and 860 DF,  p-value: < 2.2e-16

Ici, l’affichage de summary(mylm_abs) montre les paramètres du modèle et les tests d’hypothèse associés. Ils correspondent ici à des tests de Student qui vérifient si les valeurs attendues par groupes sont différentes de la valeur pour le groupe de référence (dans le premier cas, mylm_rel) ou des tests qui vérifient si les valeurs attendues par groupe sont différentes de 0 (dans le premier cas, mylm_abs). Dans un cas comme dans l’autre, ce n’est pas typiquement ce qu’on cherche à faire pour comprendre s’il existe bel et bien un effet de \(X\) sur \(Y\)…

5.2.3.2 Tests d’hypothèse

Classiquement, on va plutôt se poser les questions suivantes:

“le facteur (dans son ensemble) a-t-il un effet sur la réponse?”
“les moyennes par groupe sont-elles significativement différentes deux à deux?” (i.e. dans ce cas on ne considère pas qu’il y a un seul groupe de référence)

Pour répondre à la première question, on peut appeler la fonction “anova” (appliquée à un objet de type “modèle linéaire”) ou la fonction “aov” (remarquez que les deux lignes de commande suivantes renvoient exactement les mêmes résultats):

anova(lm(perlimpinpin~espece, data=broceliande))
summary(aov(perlimpinpin~espece, data=broceliande))

anova(lm(perlimpinpin~espece, data=broceliande))

## Analysis of Variance Table
## 
## Response: perlimpinpin
##            Df Sum Sq Mean Sq F value Pr(>F)  
## espece      3   3299 1099.66  2.3404  0.072 .
## Residuals 860 404075  469.85                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Pour répondre à la deuxième question, on peut appeler la fonction “TukeyHSD” (appliquée à un objet de type “aov”):

diff_2_a_2=TukeyHSD(aov(perlimpinpin~espece, data=broceliande))
diff_2_a_2

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = perlimpinpin ~ espece, data = broceliande)
## 
## $espece
##                         diff        lwr       upr     p adj
## chene-chataignier  2.4680952  -2.072516 7.0087066 0.5001838
## hetre-chataignier -2.4124870  -7.856701 3.0317268 0.6644258
## sapin-chataignier -1.8678514  -9.203889 5.4681859 0.9136588
## hetre-chene       -4.8805822 -10.053695 0.2925305 0.0725491
## sapin-chene       -4.3359465 -11.473108 2.8012149 0.4000079
## sapin-hetre        0.5446357  -7.198838 8.2881094 0.9978928

plot(diff_2_a_2)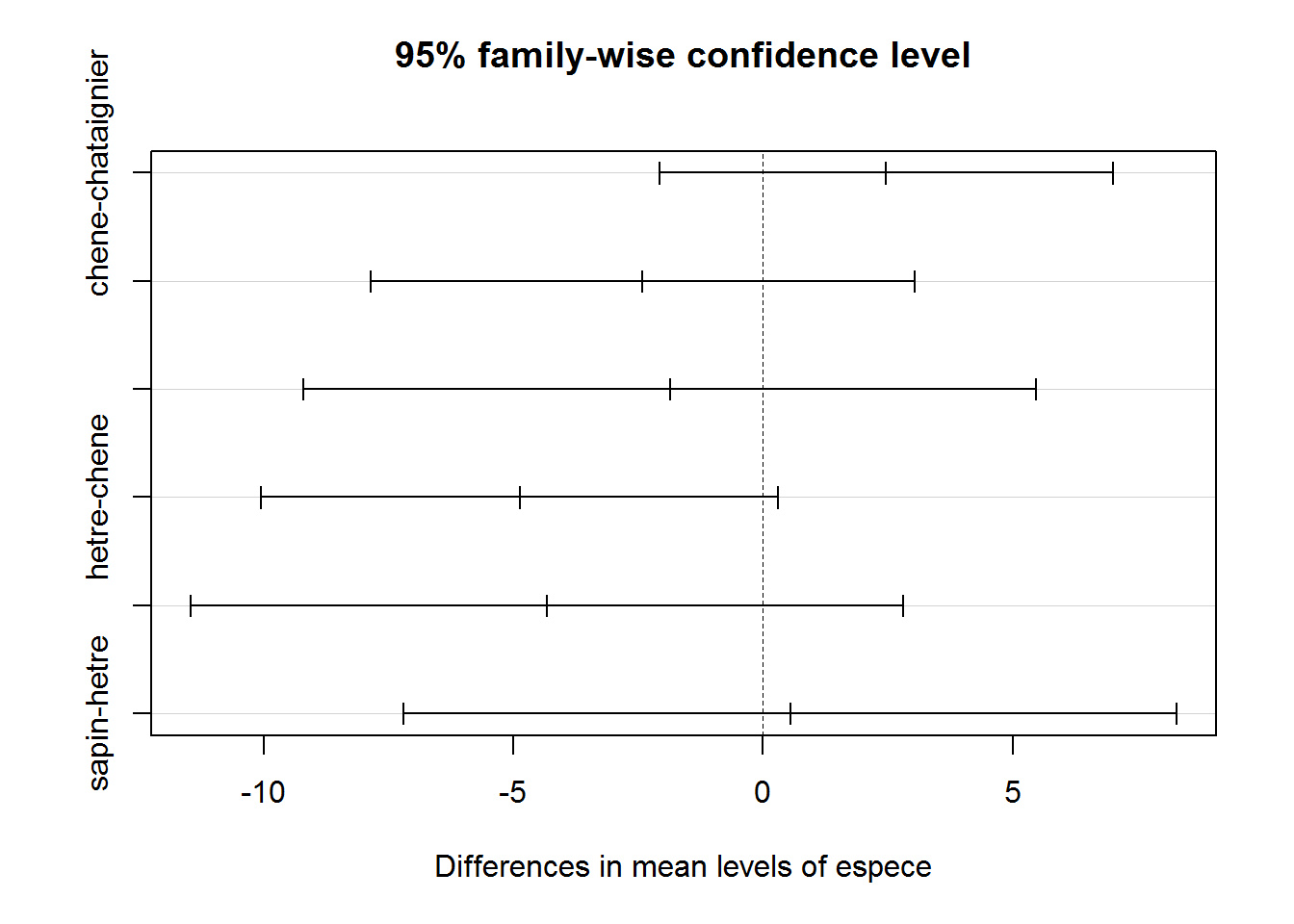

La première ligne de commande ci-dessus renvoie la p-value associée au test de Tukey HSD (HSD pour “Honestly Significant Difference”).

L’hypothèse testée, pour 2 catégories, est “La différence de moyenne entre les deux catégories est nulle”. Ainsi, la commande plot(diff_2_a_2) affiche une estimation de la différence de moyenne entre deux groupes, ainsi qu’une estimation d’un intervalle de confiance à 95% pour cette différence.

Comme pour un t-test, une p-value proche de zéro nous amène à rejeter l’hypothèse selon laquelle il n’y a pas d’effet (i.e. l’hypothèse selon laquelle il n’y a pas de différence de moyenne significative entre les groupes).

Considérez le jeu de données potions et examinez la relation entre la variable m_preparation et la variable p_destruction: est-ce que le mode de préparation de la potion semble lié à ses propriétés destructrices?…

Que pouvez-vous dire sur

le signe et la taille de l’effet?
la significativité de l’effet?
la performance de prédiction?

5.2.3.3 Et au fait, elles sont vérifiées les hypothèses du modèle linéaire?

C’est bien le moment de se poser la question, me direz-vous…

Eh bien, en l’occurence, oui, c’est bien le moment de se poser la question. En effet, ces hypothèses sont que les résidus du modèle sont distribuées de manière gaussienne, et qu’ils sont homoscédastiques. Or, les résidus “n’existent pas” tant qu’on a pas défini et calculé les paramètres du modèle… Il faut donc ajuster le modèle (moyennant quelques lignes de code) avant de se demander s’il est valide…

Examinons donc les résidus du modèle. Globalement, si les résidus sont, grosso modo, gaussiens, l’hypothèse d’homoscédasticité en revanche n’est pas respectée. Néanmoins, compte tenu du nombre de points de mesure, et de la grandeur d’effet de l’espece sur la concentration en poudre de perlimpinpin (qui apparaît clairement sur le graphe), un modèle linéaire peut, a priori, être utilisé sans trop d’inquiétudes…