Chapter 4 Etablir le lien entre deux variables: tests d’hypothèse
Avant de me lancer sur les modèles statistiques, je vais tenter d’expliquer le principe des tests d’hypothèse.
L’objectif des tests d’hypothèse est de déterminer si un effet observé à l’échelle de l’échantillon résulte d’un effet réel à l’échelle de la population, autrement dit, il s’agit de déterminer si l’effet observé est significatif et non pas simplement lié à l’aléa d’échantillonnage.
4.1 Tests d’hypothèse paramétriques: exemple du t-test
Bien qu’il existe une multitude de tests d’hypothèses (test de Student, test du Chi-2, test de Mann-Whitney, etc. en fonction du type de données et de la problématique considérés), la logique et les “mécanismes d’interprétation” sont toujours les mêmes…
Je vais donc décrire en détail les idées sous-jacente à un test statistique, en développant l’exemple d’un test particulier, le t-test.
Le t-test (ou test de Student) est conçu pour tester des différences de moyennes entre deux groupes.
Par exemple, on cherche à savoir si la quantité de poudre de perlimpinpin dans un arbre est liée à la présence d’un enchantement (comme la figure vue en section 3.2.1 le suggérait):
ggplot(broceliande, aes(x=enchantement, y=perlimpinpin))+
geom_boxplot(fill="lightblue")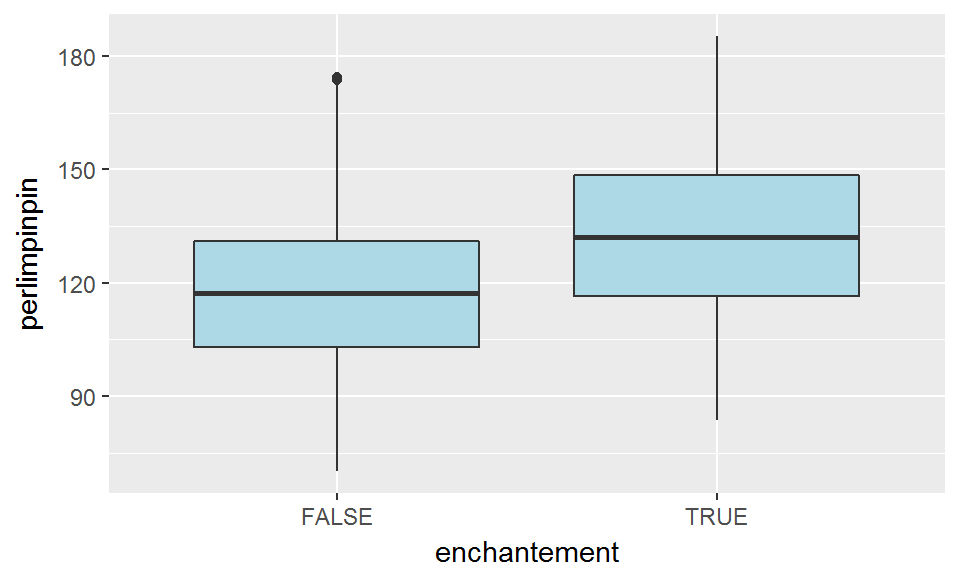
4.1.1 Le t-test en théorie
Je “conceptualise” mon problème par le modèle suivant:
\(perlimpinpin\) a une distribution \(\mathcal{N}(\mu_e,\sigma_e)\) pour les arbres enchantés, et \(\mathcal{N}(\mu_f,\sigma_f)\) pour les autres.
Je définis mon hypothèse:
\(H_0:\{\mu_e=\mu_f\}\)
Selon cette hypothèse, il n’y a pas de différence réelle de moyenne entre les deux groupes (même si, de facto, il y a une différence observée).
Autrement dit, l’hypothèse que je cherche à tester statistiquement est celle selon laquelle “la quantité de perlimpinpin moyenne n’est pas différente selon les groupes” … alors que mon hypothèse au sens “scientifique” était plutôt l’hypothèse inverse puisque j’ai en réalité l’intention de prouver que l’enchantement a un effet significatif sur la quantité de perlimpinpin!… Il faut donc faire attention à ne pas se mélanger les pinceaux…
Considérons la statistique suivante:
\[ T=\frac{\bar X_e-\bar X_f}{\sqrt{\frac{s_e^2}{n_e}+\frac{s_f^2}{n_f}}}=\frac{\bar X_e-\bar X_f}{\sqrt{eqm_e+eqm_f}} \]
où
- \(\bar{X_e}\) et \(\bar{X_f}\) sont les estimateurs de la moyenne (par groupe)
- \(s_e\) et \(s_f\) sont les estimateurs des écarts-types (par groupe)
- \(n_e\) et \(n_f\) sont les effectifs observés (par groupe)
Cette métrique est donc d’autant plus grande (en valeur absolue) que
- l’écart entre moyennes est important,
- les tailles d’échantillons sont importantes,
- la variance au sein de chaque groupe est petite.
Si notre hypothèse \(H_0\) était vraie alors cette statistique \(T\) devrait suivre une distribution de Student avec \(\nu\) degrés de liberté.
(Il s’agit d’un résultat mathématique, que je ne démontrerai pas ici!)
Le paramètre \(\nu\) correspond à:
\[ \nu=\frac{\left(\frac{s_e^2}{n_e}+\frac{s_f^2}{n_f}\right)^2}{{(\frac{s_e^2}{n_e})}^2\frac{1}{n_e-1}+{(\frac{s_f^2}{n_f})}^2 \frac{1}{n_f-1}}=\frac{(eqm_e+eqm_f)^2}{eqm_e^2\ \frac{1}{n_e-1}+eqm_f^2\ \frac{1}{n_f-1}} \]
On peut calculer les valeurs \(t_{obs}\) (valeur de \(T\) pour les observations) et \(\nu\) “à la main”:
broc_test=broceliande %>%
group_by(enchantement) %>%
summarise(m=mean(perlimpinpin),
s2=sd(perlimpinpin)^2,
n=n()) %>%
mutate(eqm=s2/n,
w=1/(n-1)) %>%
mutate(eqmw=w*eqm^2)
valeurs_obs=broc_test %>%
summarise(t_obs=diff(m)/sqrt(sum(eqm)),
nu=sum(eqm)^2/sum(eqmw))
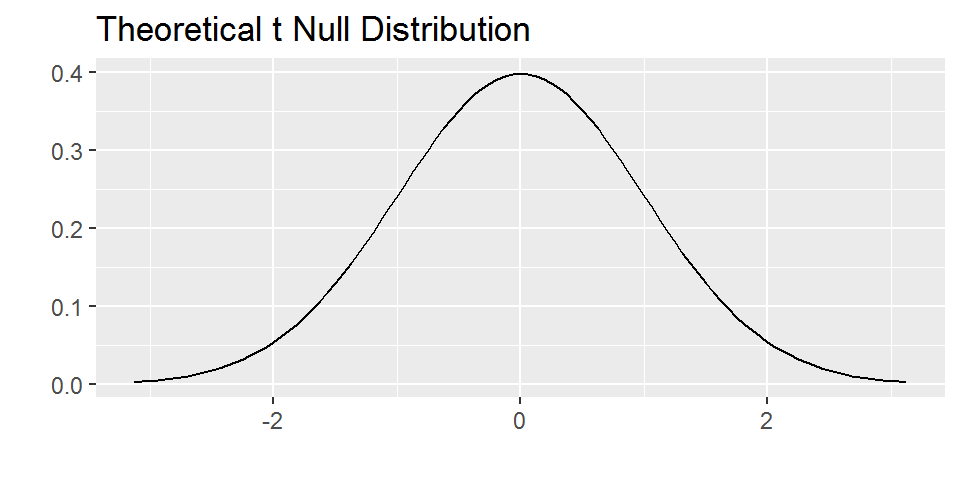
valeurs_obs## # A tibble: 1 x 2
## t_obs nu
## <dbl> <dbl>
## 1 2.01 164Voici donc la distribution de Student à \(\nu\)=164 degrés de liberté (i.e. la distribution que \(T\) doit suivre, théoriquement, si l’hypothèse \(H_0\) est vraie):
Par rapport à cette distribution théorique de \(T\) “sous hypothèse \(H_0\)”, voilà comment se situe la valeur observée de T pour notre échantillon (\(t_{obs}\)):
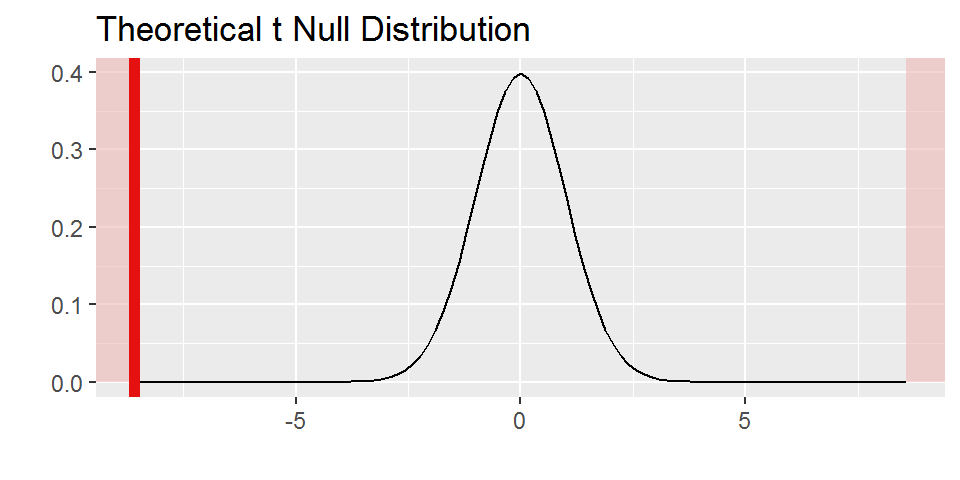
Comme on peut le voir sur ce graphique, la valeur que l’on observe pour T est plutôt “excentrée” par rapport à la distribution théorique sous hypothèse \(H_0\).
En effet, la probabilité d’observer une valeur au moins aussi excentrée (à droite ou à gauche) sous hypothèse \(H_0\), ou p-value est de:
2*(1-pt(valeurs_obs$t_obs,valeurs_obs$nu))## [1] 0.04594002C’est cette valeur de probabilité qui est représentée par la surface coloriée en rouge dans le graphique ci-dessus.
Si la p-value est particulièrement petite, cela tend à prouver que la valeur observée de \(T\) est peu probable sous hypothèse \(H_0\). Cela amène donc à remettre en question l’hypothèse (et non l’observation!!).
En dessous d’un certain seuil pour cette probabilité (par exemple, \(\alpha=5\)%), on décide de rejeter l’hypothèse \(H_0\). Dans ce cas on peut affirmer qu’il existe bien un effet significatif de enchantement sur perlimpinpin.
La valeur \(\alpha\) est souvent, par convention, 5% (il arrive aussi que l’on voie 10%, 1%, etc.). Cette valeur n’est pas un repère absolu en dessous duquel tout serait merveilleux et au dessus duquel tout serait perdu… J’y reviendrai un peu plus tard…
4.1.2 Erreurs associées à un test d’hypothèse
Cette valeur seuil \(\alpha\) abordée précédemment correspond en fait à un risque d’erreur de type I que l’on est “prêt à accepter”.
Faire une erreur de type I, ça consiste à rejeter l’hypothèse nulle alors qu’elle est vraie (c’est-à-dire, affirmer qu’une différence est significative alors que ce n’est pas le cas). Le risque d’erreur de type I est souvent noté \(\alpha\)
Faire une erreur de type II, au contraire, ça consiste à ne pas rejeter l’hypothèse nulle alors qu’elle est fausse (c’est-à-dire, ne pas conclure que la différence est significative alors qu’elle existe vraiment). Le risque d’erreur de type II est souvent noté \(\beta\).
| Cas | \(H_0\) rejetée | \(H_0\) acceptée |
|---|---|---|
| \(H_0\) vraie | erreur de type I (\(\alpha\)) | CORRECT |
| \(H_0\) fausse | CORRECT | erreur de type II (\(\beta\)) |
La puissance d’un test est égale à 1-\(\beta\) i.e. elle correspond à la probabilité de détecter un effet quand il existe (\(H_0\) est fausse et onR rejette \(H_0\)).
Quand on choisit de réaliser un test avec un risque \(\alpha\) particulièrement bas, alors le risque \(\beta\) est particulièrement élevé: alors on le fait au détriment de la puissance du test (c’est-à-dire que plus on minimise le risque de dire qu’il y a un effet alors qu’il n’y en a pas, plus on maximise le risque de “passer à côté” d’un effet qui existe).
4.1.3 Le t-test en pratique
En pratique, pour réaliser un t-test sous R, on n’a pas besoin de faire à la main toutes les étapes du calcul détaillé dans le paragraphe précédent (ouf!). Il existe évidemment des fonctions dans R pour faciliter la tâche.
La fonction de base est t.test():
mytest=t.test(perlimpinpin~enchantement, data=broceliande)
print(mytest)##
## Welch Two Sample t-test
##
## data: perlimpinpin by enchantement
## t = -2.0112, df = 164.24, p-value = 0.04594
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -7.73760812 -0.07121911
## sample estimates:
## mean in group FALSE mean in group TRUE
## 106.6673 110.5717Plusieurs informations s’affichent:
- le nom du test (t-test de Welch pour deux échantillons)
- certains éléments qui interviennent dans le calcul d’une p-value (valeur de métrique observée t, nombre de degrés de liberté df)
- la p-value elle-même
- l’hypothèse alternative (et non pas \(H_0\)) selon laquelle la différence de moyenne entre les groupes n’est pas égale à 0
- un intervalle de confiance à 95% pour cette différence de moyenne
- les moyennes estimées pour chaque groupe
On retrouve notamment la valeur \(t_{obs}\), \(\nu\) (nombre de degrés de liberté) et la p-value calculés “à la main” dans le paragraphe précédent:
mytest$p_value## NULLmytest$statistic## t
## -2.011199mytest$t_df## NULLOutre la fonction t.test de “base”, il est également possible d’utiliser le package “infer” pour réaliser un t-test “à la tidyverse”:
mytest <- broceliande %>%
t_test(formula = perlimpinpin ~ enchantement)
print(mytest)## statistic t_df p_value alternative
## 1 -2.011199 164.2365 0.04594002 two.sidedt_obs=mytest%>%
dplyr::select(statistic) %>%
dplyr::pull()
print(t_obs)## [1] -2.011199broceliande %>%
specify(perlimpinpin ~ enchantement) %>%
hypothesize(null = "independence") %>%
calculate(stat = "t") %>%
visualize(method = "theoretical",
obs_stat=t_obs,
direction = "two_sided")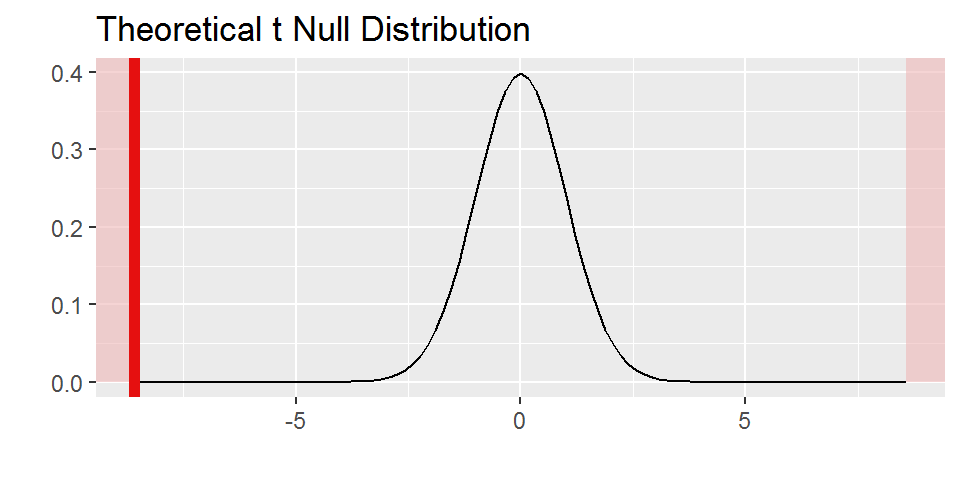
4.1.4 Les conditions d’utilisation du t-test
Revenons à la manière dont j’ai spécifié mon modèle:
\(perlimpinpin\) a une distribution \(\mathcal{N}(\mu_e,\sigma_e)\) pour les arbres enchantés, et \(\mathcal{N}(\mu_f,\sigma_f)\) pour les autres.
On a vu dans la section 4.1.1 qu’on connaissait la distribution de la statistique \(T\) sous hypothèse \(H_0\), mais aussi sous réserve que la distribution de \(perlimpinpin\) dans chaque groupe défini par \(enchantement\) soit normale.
Que se passe-t-il si ce n’est pas le cas?
Eh bien, en fait, comme dans le cas du Théorème Central Limite (voir section 2.3.2), quand bien même l’hypothèse de normalité des résidus ne serait pas respectée, la distribution de \(T\) tend bien vers une distribution de Student à \(\nu\) degrés de liberté pour des tailles d’échantillon “suffisamment grandes”.
Tout le sel de la situation consiste à estimer la valeur pour laquelle on estime que la taille d’échantillon est “suffisamment grande” (ce seuil étant d’autant plus élevé que la distribution des résidus est éloignée de la distribution normale) pour pouvoir appliquer le t-test quand bien-même l’hypothèse de normalité ne serait pas respecté…
4.1.5 Principe général d’un test d’hypothèse paramétrique
- On considère un modèle statistique décrivant nos données
- On considère une certaine hypothèse \(H_0\) concernant les paramètres du modèle
- On considère une métrique \(S\) (il s’agit d’une variable aléatoire), dont la nature dépend du test réalisé.
- On calcule sa distribution théorique en se basant sur le modèle assorti de l’hypothèse \(H_0\).
- On calcule la valeur prise par \(S\) pour les observations: on obtient ainsi la mesure \(S_{obs}\). \(S_{obs}\) est une réalisation de la variable \(S\).
- On regarde où se place \(S_{obs}\) par rapport à distribution théorique de \(S\): on calcule la probabilité que \(S\) soit au moins aussi “extrême” que \(S_{obs}\). C’est cette probabilité qui constitue la p-value.
Dans tous les cas, lorsque l’on réalise un test statistique, il faut être très attentif aux éléments suivants:
- Les hypothèses du modèle sous-jacent au test (par exemple, pour le t-test, la variable d’intérêt doit être de distribution gaussienne. En revanche, le fait que vous utilisiez le t-test de Welch et non de Student vous permet de supposer que la variance est différente dans les deux groupes)
- La nature de l’hypothèse \(H_0\) (Si vous vous trompez sur la nature de cette hypothèse, alors vous vous tromperez dans la manière dont vous interprétez les résultats du test!)
4.2 Tests non-paramétriques: exemple du test U de Mann-Whitney
4.2.1 A quoi sert-il?
Le test U de Mann-Whitney (aussi appelé test de la somme des rangs de Wilcoxon ou plus simplement test de Wilcoxon) sert à tester l’hypothèse selon laquelle la distribution des données est la même pour deux groupes.
La p-value associée à ce test va ainsi répondre à la question suivante:
Si les données pour les deux groupes étaient issues d’une même population, quelle serait la probabilité que l’on observe par hasard une différence de rangs(ou localisations) entre les deux groupes aussi forte que celle observée sur les données?
Le test U de Mann-Whitney est souvent utilisé comme solution alternative à l’utilisation d’un t-test dans le cas où les données ne sont pas distribuées selon une loi normale et/ou dans le cas où les données sont peu nombreuses.
Il s’agit en effet d’un test non-paramétrique, qui ne repose ni sur une hypothèse de distribution gaussienne des données par groupe, ni sur une propriété asymptotique.
4.2.2 Un exemple
Considérons une sous-partie du jeu de données brocéliande: ici, on va s’intéresser uniquement aux chênes enchantés, et étudier le lien entre feerie(groupe A: pas de fée, groupe B: au moins une fée) et âge:
chenes_enchantes=broceliande %>%
filter(espece=="chene",enchantement) %>%
mutate(feerie=factor(fees>=1, labels=c("A","B"))) %>%
select(feerie,age)
ggplot(chenes_enchantes, aes(x=feerie, y=age))+
geom_boxplot(fill=c("grey","aquamarine"))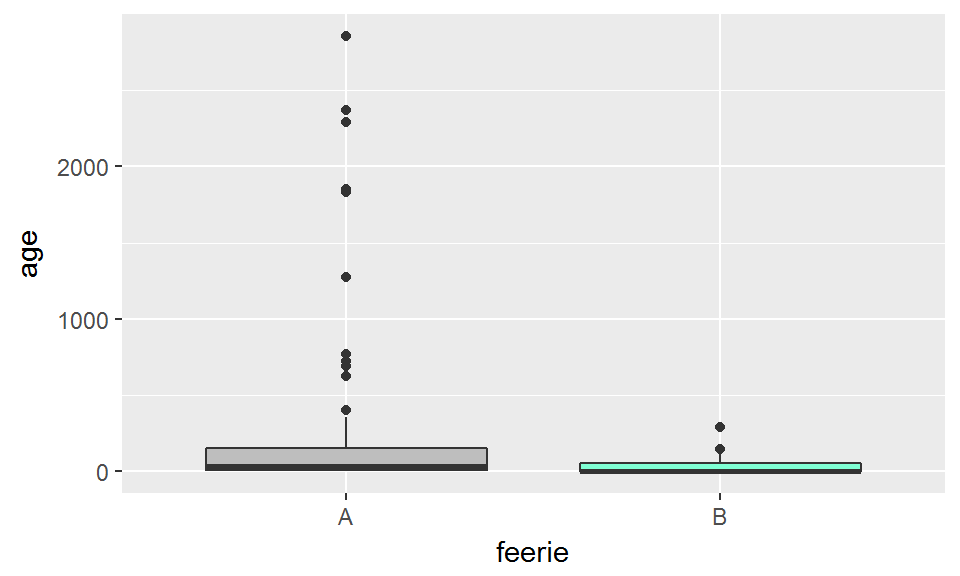
On a ici des données qui ne sont ni franchement nombreuses, ni franchement normales.
4.2.2.1 Sur quelle métrique le test de Mann-Whitney se base-t-il?
Le test U de Mann-Whitney calcule une p-value qui se base non pas sur les données brutes, mais sur leurs rangs. Les rangs en question correspondent à l’emplacement de chaque donnée au sein de la série lorque cette série est ordonnée par ordre croissant.
chenes_enchantes=chenes_enchantes %>%
mutate(rang_age=min_rank(age))
head(chenes_enchantes)## feerie age rang_age
## 1 A 20.9421255 29
## 2 A 50.6511805 40
## 3 A 3.5383734 18
## 4 A 0.2901871 4
## 5 A 33.5007258 33
## 6 A 1.7073722 11Les distributions des rangs sont beaucoup moins affectées par l’existence de valeurs extrêmes que ne le sont les distributions des valeurs brutes:
ggplot(chenes_enchantes, aes(x=feerie, y=rang_age))+
geom_boxplot(fill=c("grey","aquamarine"))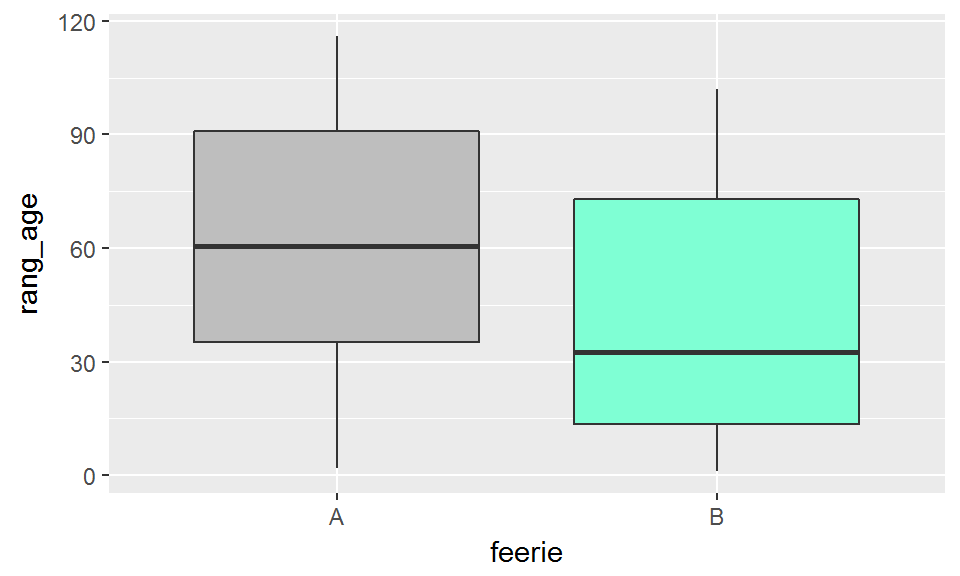
Représentons les rangs des individus ainsi que l’appartenance de ces individus aux deux groupes. Les pointillés représentent la moyenne des rangs pour chacun des groupes
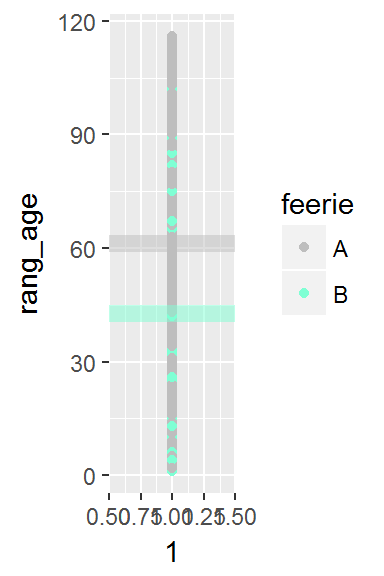
Le test de Mann-Whitney peut se baser sur une métrique \(W\) (en lien avec la dénomination “test de Wilcoxon”) qui correspond à
\[ W=W_A=\sum_{i=1}^{n}\mathbf{1}_A R_i-n_A(n_A+1)/2\\ \]
On peut aussi définir \(W_B\) :
\[ W_B=\sum_{i=1}^{n}\mathbf{1}_B R_i-n_B(n_B+1)/2 \]
Les nombres \(n_A(n_A+1)/2\) et \(n_B(n_B+1)/2\) correspondent en fait à ce que serait la somme des rangs si tous les individus du groupe A (respectivement B) avaient les rangs 1,2,3,….,\(n_A\) (respectivement 1,2,3,…,\(n_B\)).
\(W\) est ainsi d’autant plus grand que les individus du groupe A présente des rangs élevés au sein de l’ensemble des individus.
Alternativement, on pourrait considérer la métrique \(U\) (en lien avec la dénomination “test U de Mann-Whitney”) qui correspond à:
\[ U=min(W_A,W_B) \]
Cette métrique est quant à elle d’autant plus faible que l’un ou l’autre des groupes présente des rangs bas.
Calculons la métrique \(W\) pour nos données:
dfsummary=chenes_enchantes %>%
group_by(feerie) %>%
summarize(n=n(),
SR=sum(rang_age)) %>%
mutate(m=n*(n+1)/2) %>%
mutate(W=SR-m)
dfsummary## # A tibble: 2 x 5
## feerie n SR m W
## <fct> <int> <int> <dbl> <dbl>
## 1 A 59 2198 1770 428
## 2 B 12 358 78.0 280En l’occurence, par construction on a toujours
\[W_A+W_B=n_An_B\]
4.2.3 A quoi la p-value correspond-elle?
Supposons que le groupe A ne corresponde pas à des rangs particulièrement élevés dans la série. Dans ce cas, les rangs observés pour A sont comme “attribués au hasard”. Quelle est alors la distribution de \(W\)?
Pour répondre à cette question nous allons simuler 1000 jeux de données issus d’une réattribution au hasard des rangs dans le jeu de données initial
Nous calculerons pour chaque simulation la valeur de \(W\).
Wsim=function(i){
W_sim=chenes_enchantes %>%
mutate(rangsim=sample(1:nrow(chenes_enchantes),replace=FALSE)) %>%
group_by(feerie) %>%
summarize(n=n(),
SR=sum(rangsim)) %>%
mutate(m=n*(n+1)/2) %>%
mutate(W=SR-m) %>%
select(W) %>%
t() %>%
as.data.frame() %>%
rename(W_A=V1,W_B=V2)
return(W_sim)
}
dfsim=map(1:1000, Wsim) %>% bind_rows()
ggplot(dfsim, aes(x=W_A))+
geom_histogram(fill="lightpink")+
geom_vline(xintercept=dfsummary$W[1])+
ggtitle("distrib. de W sous hypothèse nulle")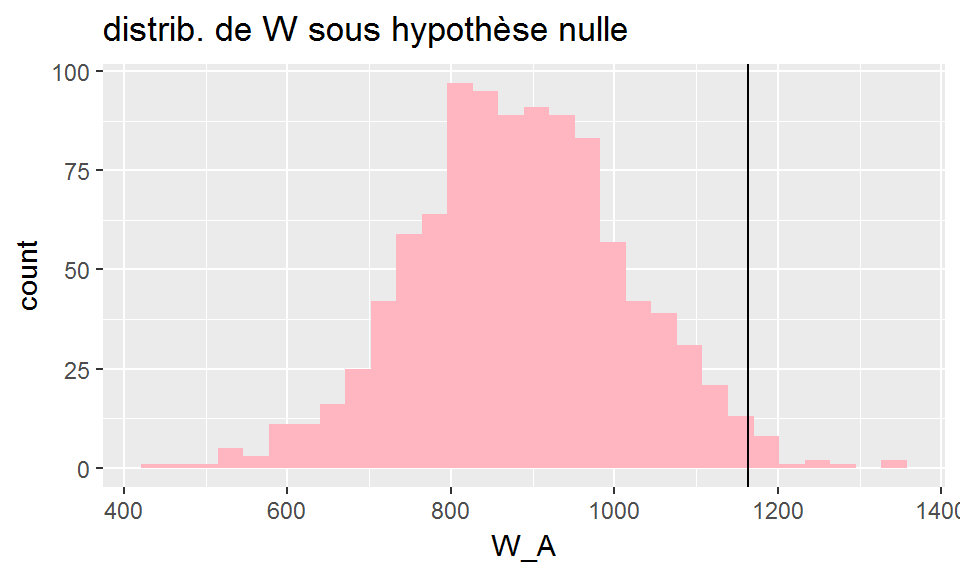
La distribution empirique de W nous permet de calculer la p-value correspondant au test de l’hypothèse “le groupe A n’a pas une localisation particulièrement élevée”.
montest=wilcox.test(age~feerie,
alternative="greater",
data=chenes_enchantes)
print(montest)##
## Wilcoxon rank sum test with continuity correction
##
## data: age by feerie
## W = 428, p-value = 0.1297
## alternative hypothesis: true location shift is greater than 0print(length(which(dfsim$W_A>=montest$statistic))/1000)## [1] 0.138Ici on veut en fait faire un test bilatéral : notre hypothèse nulle “la distribution des données est la même pour les deux groupes” correspond en fait à deux sous-hypothèses:
- “le groupe A n’a pas une localisation particulièrement élevée” ET
- “le groupe A n’a pas une localisation particulièrement basse” (i.e. “le groupe B n’a pas une localisation particulièrement élevée”)
On s’interroge ainsi non seulement sur la distribution de \(W_A\) mais aussi sur la distribution de \(W_B\).
Or ces deux distributions sont en fait les mêmes…
On peut ainsi retrouver la p-value fournie par le test:
montest=wilcox.test(age~feerie,
alternative="two.sided",
data=chenes_enchantes)
print(length(which(dfsim$W_A>=montest$statistic))/1000)## [1] 0.138print(length(which(dfsim$W_B<=montest$statistic))/1000)## [1] 0.8714.2.5 Comment R calcule-t-il la p-value?
Ci-dessus, j’ai montré comment on peut recalculer “à la main” la p-value fournie par le test. En fait, pour des valeurs de \(n_A\) et \(n_B\) assez élevées, la distribution de W est approximativement normale (R n’a pas besoin d’effectuer des simulations, comme nous l’avons fait, pour calculer la p-value).
Pour des valeurs de \(n_A\) et \(n_B\) relativement faibles, les p-values sont tabulées (c’est-à-dire que pour des valeurs \(n_A\) et \(n_B\) faibles, R a en mémoire les quantiles de la distribution de W). Cependant, de la même manière que dans nos simulations ci-dessus, ces p-values ont été calculées en supposant qu’il n’y avait pas d’ex-aequos (i.e. pour calculer ces quantiles, il a été supposé que les rangs étaient 1,2,3,….,n, et non, par exemple, 2,2,2,3,4,5,…,n). C’est la raison pour laquelle R affiche des Warnings dans le cas où
- les données sont peu nombreuses ET
- il y a des ex-aequos.
# xA=c(1.5,6.3,6.3,2.7)
# xB=c(2.5,3.3,1.3,2.1,5.7,1.1)
# nA=length(xA)
# nB=length(xB)
# n=nA+nB
# groupes=c(rep("A",nA),rep("B",nB))
# x=c(xA,xB)
#
# wilcox.test(x~groupes)Pour des échantillons plus grands, on n’a pas ce même message d’erreur car la p-value est calculée en se basant sur l’approximation normale:
xA=rlnorm(50,3,2)
xB=rlnorm(50,4,2)
xA[1:10]=xA[11:20]
nA=length(xA)
nB=length(xB)
n=nA+nB
groupes=c(rep("A",nA),rep("B",nB))
x=c(xA,xB)
wilcox.test(x~groupes)##
## Wilcoxon rank sum test with continuity correction
##
## data: x by groupes
## W = 886, p-value = 0.01221
## alternative hypothesis: true location shift is not equal to 04.2.6 Comparaison
t.test(age~feerie, data=chenes_enchantes)##
## Welch Two Sample t-test
##
## data: age by feerie
## t = 2.5065, df = 67.926, p-value = 0.01459
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 38.72121 341.12816
## sample estimates:
## mean in group A mean in group B
## 258.21505 68.29037wilcox.test(age~feerie, data=chenes_enchantes)##
## Wilcoxon rank sum test with continuity correction
##
## data: age by feerie
## W = 428, p-value = 0.2594
## alternative hypothesis: true location shift is not equal to 04.3 Etablir le lien entre deux variables catégorielles
Intéressons-nous au jeu de données fantaisie, et au lien entre sexe et activite que nous avons déjà décrit dans la section 3.3.
4.3.1 Tableau de contingence
Nous avons-vu que la comparaison entre le tableau des effectifs croisés observés et des effectifs attendus sous hypothèse d’indépendance pouvait nous renseigner sur un lien éventuel entre les deux variables considérées.
En l’occurrence, on peut noter les effectifs observés dans chacune des J cases du tableau \[\bar {N_i}\] et les effectifs attendus \[N_i\].
A partir de ces deux tableaux, une statistique du Chi-2 (des fois écrit \(\chi^2\)) peut être calculée et utilisée pour tester l’hypothèse d’indépendance entre les deux variables catégorielles. La statistique du \(\chi^2\) correspond à :
\[T=\sum_{i=1}^{J}\frac{(\bar{N_i}-N_i)^2}{N_i}\] Sous hypothèse d’indépendance, et sous réserve que les effectifs par case soient suffisamment importants, cette statistique \(T\) est censée suivre une distribution du \(\chi^2\) à \(J-2\) degrés de liberté.
C’est ce résultat (mathématique) qui permet de fournir une p-value qui correspond à la probabilité d’obtenir une valeur de \(T\) supérieure à celle qui est calculée sur les observations.
4.3.2 Faire un test du Chi-2 sous R
montest=chisq.test(table(fantaisie$sexe,fantaisie$activite))
print(montest)##
## Pearson's Chi-squared test
##
## data: table(fantaisie$sexe, fantaisie$activite)
## X-squared = 26.136, df = 3, p-value = 8.931e-06obs_chisq=fantaisie %>%
chisq_test(formula=activite~sexe) %>%
select(statistic) %>%
pull()
truc=fantaisie %>%
specify(activite~sexe) %>%
hypothesize(null="independence") %>%
generate(reps=1000, type="permute") %>%
calculate(stat="Chisq") %>%
visualize(obs_stat=obs_chisq, direction="greater")4.3.3 Petits effectifs
fantaisie_princiere=filter(fantaisie, activite=="royaute") %>%
mutate(tenue=as.factor(as.vector(tenue)))
obs_chisq=fantaisie_princiere %>%
chisq_test(formula=tenue~sexe) %>%
select(statistic) %>%
pull()
truc=fantaisie_princiere %>%
specify(tenue~sexe) %>%
hypothesize(null="independence") %>%
generate(reps=1000, type="permute") %>%
calculate(stat="Chisq") %>%
visualize(obs_stat=obs_chisq, direction="greater")
4.2.4 Comment faire un test U de Mann-Whitney sous R?
Ici, la p-value est plus grande que 0.05: on ne parvient pas à rejeter l’hypothèse selon laquelle les données des deux groupes proviennent d’une même distribution au seuil \(\alpha=0.05\).